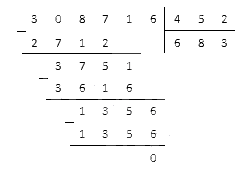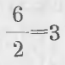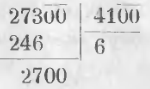Что такое делить нацело
Математика. 5 класс
Конспект урока
Перечень вопросов, рассматриваемых в теме:
— деление натуральных чисел;
— свойства деления натуральных чисел.
Деление – это математическое действие, обратное умножению.
Делимое – это число, которое делят.
Делитель – это число, на которое делят.
Частное – результат деления.
Делить на нуль нельзя.
Любое натуральное число а делится на 1 и само на себя:
Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число: частное от этого не изменится.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что нам уже известно об операции деления. Пусть у нас есть натуральные числа a и b, причём а больше b или равно b (a ≥ b). Говорят, что а делится на b нацело, если существует натуральное число с, при умножении которого на b получается а: a = b ∙ c.
Обычно слово «нацело» в этой фразе опускается. При этом записывают: a : b = с и называют а – делимым, b – делителем, с – частным.
Любое натуральное число а делится на 1 и само на себя:
так как а ∙ 1 = а, 1 ∙ а = а.
Например, 14 делится на 1 и на 14.
14 : 1 = 14, 14 : 14 = 1
При делении ноля на любое натуральное число получается ноль: 0 : а = 0, потому что 0 ∙ а = 0.
Запомните: делить на нуль нельзя!
Любое натуральное число а делить на нуль нельзя, потому что не существует такого числа с, для которого выполнялось бы равенство а : 0 = с (так как с ∙ 0 = 0 ≠ а). Принято считать, что нуль на нуль делить нельзя.
Для деления чисел из двух и более цифр (знаков) применяют деление уголком.
Вспомним, как делить уголком, на примере.
Для начала запишем делимое и делитель уголком:
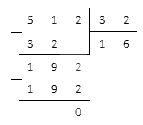
Начнём делить 392 на 28 следующим образом.
Во-первых, определим неполное частное. Для этого слева направо сравниваем цифры делимого и делителя.
Рассмотрим цифру 3. Она меньше 28 – значит, нужно взять ещё одну цифру из делимого. 39 больше 28, следовательно, это неполное частное.
Ставим точку в частном (под уголком делителя).
Посчитаем, сколько цифр осталось в делимом, после неполного частного. У нас после 39 стоит только одна цифра – 2. Значит, и в результат добавляем ещё одну точку.
Приступаем к делению: 28 помещается в 39 только один раз, поэтому ставим первой цифрой ответа единицу и вычитаем 28 из 39.
После вычитания в остатке получилось 11, это меньше, чем 28, поэтому к 11 дописываем 2.
112 делится на 28. Получаем 4. Записываем полученный результат второй цифрой в ответе.
В остатке получился нуль – значит, числа разделились нацело. Таким образом, 392 : 28 = 14.
Важное свойство частного: делимое и делитель можно одновременно умножить или разделить на одно и то же натуральное число: частное от этого не изменится.
Сначала одновременно умножим 50 и 25 на 2. Получим:
Теперь разделим 50 и 25 на 5. Получим:
В обоих случаях ответ оказался одинаковым. Значит, свойство частного верно.
Если каждое из натуральных чисел a и b делится на натуральное число с, то верно равенство:
(a+ b) : c = a : c + b : c.
Убедимся в правдивости данного свойства на примере.
Вычислим выражение: 124 : 4 + 36 : 4.
Рассмотрим два способа решения.
1 способ. Выполним деление и сложим результаты.
124 : 4 + 36 : 4 = 31 + 9 = 40.
2 способ. Заметим, что у нас есть общий делитель – 4. Вынесем его за скобки. Получим:
(124 + 36) : 4 = 160 : 4 = 40.
В обоих случаях у нас получился один и тот же ответ. Значит, свойство верно.
Разбор решения заданий тренировочного модуля
№ 1. Вычислите 812 : 14 = _____.
Решение: выполним деление уголком.
№ 2. Найдите неизвестный множитель х из равенства: 15 ∙ х = 195.
Выберите верный ответ: х = 3; х = 13; х = 25; х = 15.
Решение: чтобы найти неизвестный множитель, надо произведение поделить на известный множитель, то есть:
Деление натуральных чисел: правила, примеры, решения
В этой статье мы рассмотрим правила и алгоритмы деления натуральных чисел. Сразу отметим, что здесь мы смотрим только на деление нацело, то есть без остатка. О делении натуральных чисел с остатком читайте в нашем отдельном материале.
Для каждого случая приведем и подробно рассмотрим примеры. В конце статьи покажем, как проводить проверку результата деления.
Связь деления с умножением
Чтобы проследить связь между делением и умножением, вспомним, что деление представляется, как разбиение исходного делимого множества на несколько одинаковых множеств. Умножение связано с объединением нескольких одинаковых множеств в одно.
Обратный процесс разбиения полученного общего множества на b множеств по с предметов в каждом соответствует делению:
На основе сказанного можно перейти к следующему утверждению:
Пользуясь переместительным свойством умножения, можно записать:
Подытожим все изложенное выше и дадим определение деления натуральных чисел.
Деление натуральных чисел
Это определение станет базой, на основе которой мы будем строить правила и методы деления натуральных чисел.
Деление методом последовательного вычитания
Иными словами данную задачу можно сформулировать так: имеется 12 предметов (например, апельсинов), и их нужно разделить на равные группы по 4 предмета (разложить в коробки по 4 штуки). Сколько будет таких групп или коробок по четыре апельсина в каждой?
Шаг за шагом будем отнимать от исходного количества по 4 апельсина и формировать группы по 4 до того момента, пока апельсины не закончатся. Количество шагов, которые нам придется сделать, и будет ответом на изначальный вопрос.
Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.
При делении методом последовательного вычитания количество операций вычитания до получения нулевого остатка и есть частное от деления.
Для закрепления рассмотрим еще один, более сложный пример.
Пример 1. Деление последовательным вычитанием
Вычислим результат деления числа 108 на 27 методом последовательного вычитания.
Более действий не требуется. Мы получили ответ:
Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.
Деление равных натуральных чисел
Согласно свойствам натуральных чисел, сформулируем правило, как делить равные натуральные числа.
Деление равных натуральных чисел
Частное от деления натурального числа на равное ему натуральное число равно единице!
Деление на единицу
Основываясь на свойствах натуральных чисел, можно также сформулировать правило деление натурального числа на единицу.
Деление натурального числа на единицу
Частное от деления любого натурального числа на единицу равно самому делимому числу.
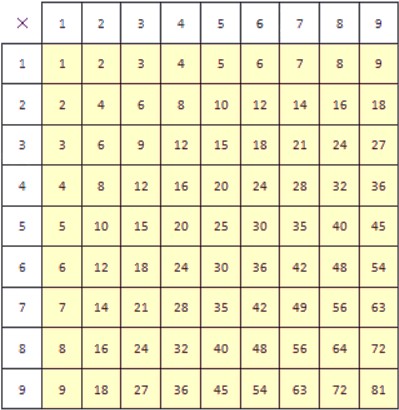
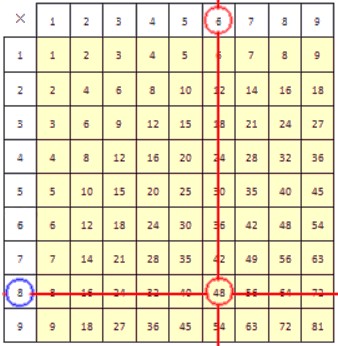
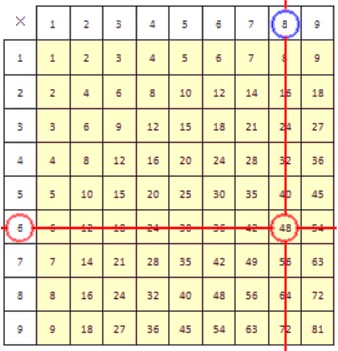
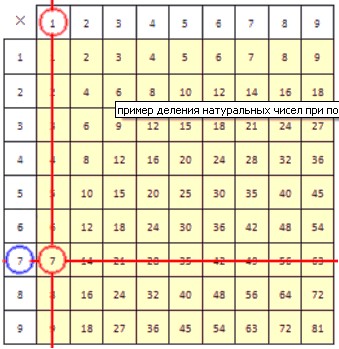
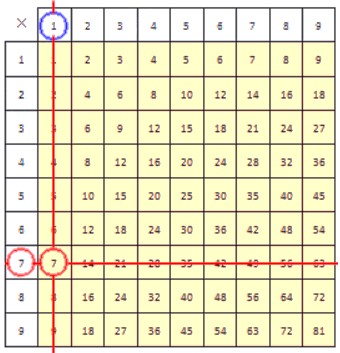
Деление с помощью таблицы умножения
С помощью таблицы умножения можно проводить деление любого числа на желтом фоне на любое однозначное натуральное число. Покажем, как это делать. Есть два способа, применение которых мы будем рассматривать на примерах.
Настоятельно рекомендуем выучить таблицу умножения!
Деление на 10, 100, 1000 и т.д.
Деление на 10, 100, 1000 и т.д.
Отбрасывается столько нулей, сколько из есть в записи делителя!
Представление делимого в виде произведения
При делении натуральных чисел не стоит забывать о свойстве деления произведения двух чисел на натуральное число. Иногда делимое можно представить в виде произведения, один из множителей в котором делится на делитель.
Рассмотрим типичные случаи.
Пример 2. Представление делимого в виде произведения
Имеем: 30 ÷ 3 = 3 · 10 ÷ 3
Воспользовавшись свойством деления произведения двух чисел, получаем:
3 · 10 ÷ 3 = 3 ÷ 3 · 10 = 1 · 10 = 10
Приведем еще несколько аналогичных примеров.
Пример 3. Представление делимого в виде произведения
7200 ÷ 72 = 72 · 100 ÷ 72 = 72 ÷ 72 ÷ 100 = 100
1600000 = 160 · 10000
1600000 ÷ 160 = 160 · 10000 ÷ 160 = 160 ÷ 160 · 10000 = 10000
В более сложных примерах удобно пользоваться таблицей умножения. Проиллюстрируем это.
Пример 5. Представление делимого в виде произведения
Теперь закончим деление:
5400 ÷ 9 = 54 · 100 ÷ 9 = 54 ÷ 9 · 100 = 6 · 100 = 600
Для закрепления данного материала рассмотрим еще один пример, уже без подробных словесных пояснений.
Пример 6. Представление делимого в виде произведения
120 ÷ 4 = 12 · 10 ÷ 4 = 12 ÷ 4 · 10 = 3 · 10 = 30
Деление натуральных чисел, оканчивающихся на нуль
Как всегда, поясним это на примерах.
Пример 7. Деление натуральных чисел, оканчивающихся на 0
Используя свойство деления натурального числа на произведение, можно записать:
Деление на 10 мы уже разобрали в предыдущем пункте.
490 ÷ 10 ÷ 7 = 49 ÷ 7 = 7
Для закрепления разберем еще один, более сложный пример.
Пример 8. Деление натуральных чисел, оканчивающихся на 0
Возьмем числа 54000 и 5400 и разделим их.
Представим 5400 в виде 54 · 100 и запишем:
Теперь делимое 540 представляем в виде 54 · 10 и записываем:
540 ÷ 54 = 54 · 10 ÷ 54 = 54 ÷ 54 · 10 = 10
Подведем итог по изложенному в данном пункте.
Если в записях делимого и делителя справа присутствуют нули, то нужно избавиться от одинакового количества нулей как в делимом, так и в делителе. После этого выполнить деление получившихся чисел.
Метод подбора частного
Прежде чем рассматривать этот способ деления, введем некоторые условия.
Пример 9. Подбор частного
Начнем подбор частного.
27 · 1 = 27 27 · 2 = 54 27 · 3 = 81 27 · 4 = 108
Бинго! Частное найдено методом подбора:
Отметим, что в случаях, когда b · 10 > a частное также удобно находить методом последовательного вычитания.
Представление делимого в виде суммы
Результаты делений в скобках известны нам из проведенных ранее действий.
Рассмотрим еще несколько примеров, уже не комментируя каждое действие столь детально.
Пример 10. Деление натуральных чисел
2. Справа у делителя приписываем один нуль.
Равенство 60 ÷ 2 = 30 ещё пригодится нам в будущем.
Теперь находим частное:
31 · 10 = 310 ; 31 · 20 = 620 ; 31 · 30 = 930 ; 31 · 40 = 1240
31 · 1 = 31 ; 31 · 2 = 62 ; 31 · 3 = 93 ; 31 · 4 = 124 ; 31 · 5 = 155 ; 31 · 6 = 186 ; 31 · 7 = 217 ; 31 · 8 = 248
Постепенно увеличиваем сложность примеров.
Пример 12. Деление натуральных чисел
В данном случае описанный выше алгоритм нужно будет применить три раза. Не будем приводить все выкладки, просто укажем, в виде каких слагаемых будет представлен делитель. Вы можете проверить себя, и провести вычисления самостоятельно.
Казалось бы, мы рассмотрели практически все возможные способы деления натуральных чисел. На этом, тему можно считать закрытой. Однако, есть способ, который в ряде случаев позволяет провести деление быстрее и рациональнее.
Рассмотрим его напоследок.
Представление делимого в виде разности натуральных чисел
Иногда делимое проще и удобнее представлять в виде разности, а не суммы. Это может значительно ускорить и облегчить процесс деления. Как именно? Покажем на примере.
Пример 13. Деление натуральных чисел
Если воспользоваться алгоритмом из предыдущего пункта, мы получим в результате:
Результат тот же, но действия объективно легче и проще.
Решим еще один пример тем же методом. Отметим, что важно уметь правильно заметить, какую манипуляцию сделать с числами, чтобы провести деление легко. Скажем даже, что в этом присутствует некоторый элемент искусства.
Пример 14. Деление натуральных чисел
490 ÷ 7 = 70 7 ÷ 7 = 1
Проверка результата деления
Проверка никогда не бывает лишней, особенно, если мы делили большие числа. Как проверять, правильно ли выполнено деление натуральных чисел? При помощи умножения!
Проверка результата деления
Чтобы проверить правильно ли выполнено деление, нужно частное умножить на делитель. В результате должно получится делимое.
Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.
Смысл этого действия очень прост. Например, у нас было a предметов, и эти a предметов мы разложили на b кучек. В каждой кучке оказалось по с предметов. Математически это выглядит так:
Рассмотрим проведение проверки на двух примерах.
Пример 15. Проверка результата деления натуральных чисел
Умножим частное 25 на делитель 19 и выясним, верно ли разделили числа.
Число 475 равно делимому, значит, деление выполнено верно.
Разделите и проверьте результат:
Будем представлять делимое в виде суммы слагаемых и осуществлять деление.
Вывод: деление выполнено верно.
Проверка результата деления чисел делением
Рассмотренный выше способ проверки основан на умножении. Существует также проверка делением. Как ее проводить?
Проверка результата деления
Чтобы проверить верно ли найдено частное, нужно делимое разделить на полученное частное. В результате должен получится делитель.
Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.
Правило основано на той же связи между делимым, делителем и частным, что и правило из предыдущего пункта.
Пример 17. Проверка результата деления натуральных чисел
Верно ли равенство:
Разделим делимое на частное:
В результате получился делитель, значит, деление выполнено верно.
Представляя делимое в виде суммы, получаем:
Деление целых чисел: правила, примеры
Данная статья рассказывает о том, как делить без остатка целые числа, то есть нацело. Будут введены термины и обозначения для дальнейшего описания чисел, деление положительных и отрицательных чисел. В итоге произведем проверку вычислений.
Термины и обозначения
При делении целых чисел используются те же термины, что и при описании натуральных чисел.
Делимое – это число, над которым совершают деление.
Делитель – число, на которое делят.
Частное – результат деления.
Деление целых чисел
Между умножением и делением натуральных чисел существует связь. Это связано с тем, что при делении можно найти частное, которое при обратном действии будет считаться множителем. Иначе можно записать, что деление целых чисел служит нахождением одного из целых множителей.
Частное от деления считается целым тогда, когда получается результат без остатка, то есть целое число a должно делиться на число b с целым частным в результате.
Правила деления целых чисел
Можно сделать вывод, что необходимо использовать правила, которые позволяют производить деление целых чисел. Они позволят делить целые и натуральные числа.
Деление целых положительных чисел
Целыми положительными числами называют натуральные числа, поэтому деление целых положительных чисел производится, исходя из правил деления натуральных чисел. Рассмотрим несколько примеров для детального просмотра деления целых положительных чисел.
Решение
Когда имеем большое число, деление лучше всего производить в столбик:
Правило деления целых отрицательных чисел, примеры
Для определения знака числа с необходимо выяснить, какие знаки находятся перед делимым и делителем.
Исходя из смысла деления целых чисел, равенство b · c = a справедливо. Правило умножения целых чисел говорит о том, что частное должно быть положительным. Иначе, b · c будет производиться по правилам целых отрицательных чисел. Частное с от деления целых отрицательных целых чисел является положительным числом.
Рассмотрим несколько примеров деления отрицательных чисел.
Решение
Для решения необходимо разделить числа по модулю. Деление производится столбиком.
Правило деления целых чисел с разными знаками, примеры
Выделим правило деления целых чисел, содержащих разные знаки.
Детально разберем примеры, где необходимо применить правило деления целых чисел с разными знаками.
Решение
Данный пример показывает правильное деление целых чисел с разными знаками. Для этого необходимо применить правило
Деление нуля на целое число
Для углубления в правило рассмотрим некоторые пояснения.
Не делить на нуль
Проверка результата деления целых чисел
Проверку осуществляют умножением. Чтобы произвести проверку деления, нужно полученное частное умножить на делитель, если в результате получается число, равное делимому, тогда результат считается правильным.
Рассмотрим на примере решение с проверкой результата.
Решение
Математика
Определить, сколько раз нужно взять слагаемым меньшее число 2, чтобы получить большее число 6, значит определить, сколько раз число 2 содержится в 6, или сколько раз число 6 содержит 2.
Число 2 содержится в 6 три раза, ибо, чтобы получить 6, нужно взять сумму трех равных слагаемых:
Найти, сколько раз число 2 содержится в 6, значит разделить 6 на 2.
Определение. Деление есть такое действие, в котором по двум данным числам определяют, сколько раз одно число содержится в другом.
Данные числа в делении называются делимым и делителем, искомое называется частным.
Делимое есть то число, которое содержит другое.
Делитель есть то число, которое содержится в другом.
Частное показывает, сколько раз делитель содержится в делимом.
В данном примере делимое есть 6, делитель 2, частное 3.
Разделить 6 на 2 значит также разбить 6 на 2 равных слагаемых и отыскать их величину. Число 6 представится при помощи двух равных слагаемых в виде:
Каждое из равных слагаемых называется частью делимого.
Посредством деления целых чисел также узнается, как велико каждое слагаемое, если делимое разобьется на столько равных слагаемых, сколько в делителе единиц.
В этом случае делимое есть то число, которое делится или разбивается на равные части. Делитель показывает, на сколько равных частей делится делимое. Частное показывает, сколько приходится на каждую часть.
Способы деления
Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.
С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:
следовательно, 4 содержится в 12 три раза.
С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:
Отсюда находим, что можно вычесть 4 из 12 ровно три раза.
Деление есть сокращенное вычитание равных вычитаемых.
Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.
Различные случаи при делении
При делении целых чисел бывают два случая:
Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что деление совершилось нацело или без остатка. Умножив частное 3 на делитель 4, получаем делимое 12.
Разделяя 26 на 8, мы при последовательном вычитании получаем:
Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют остатком.
Остаток всегда меньше делителя. В этом случае говорят, что деление не совершается нацело или деление совершается с остатком.
Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.
Целое частное иногда называют просто частным.
Итак, при делении мы имеем два случая:
Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.
Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.
Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.
При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому деление есть действие, обратное умножению.
Знак деления
Действие деления изображается знаком двоеточия ÷, который ставится между делимым и делителем.
Деление числа 6 на 2 изображают письменно:
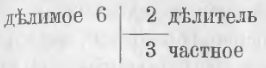
Действие деления обозначается также начертанием |–, где вертикальная черта отделяет делимое, а горизонтальная делитель от частного.
В данном примере имеем:
В нашем примере деление изображается письменно:
Знак деления прешел к нам от древних математиков.
Основные приемы при делении
Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.
Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.
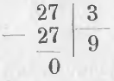
Чтобы разделить 27 на 3 мы пишем
Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое. Чтобы найти цифру частного, мы пробуем умножать делитель на разные числа или, как обыкновенно говорят, задаемся разными числами, и сравниваем произвдение делителя на частное с делимым.
Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.
Само вычисление выражают письменно:
Деление совершилось нацело.
Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.
Отыскивая целое частно, мы имеем при этом три случая:
Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:
в остатке число 7 больше делителя 4. Это показывает, что частное 5 мало и его нужно увеличить.
Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.
Взяв для частного 6, мы ход вычисления выражаем письменно:
словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:
Правило определения частного:
Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.
Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.
Если остаток меньше делителя, цифра частного верна.
Это правило показывает, что при делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя. Задаваться так, значит задаваться наибольшим целым числом.
В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и
27 = 4 × 6 + 3 = 24 + 3
Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.
Деление многозначного числа на однозначное
Частное от деления многозначного числа на однозначное иногда выражается числом, состоящим также из нескольких цифр. В этом случае деление распадается на несколько отдельных действий.
Разделим 702 на 3. Частное содержит три цифры. Оно больше 100 и меньше 1000, ибо делимое больше 300 (3 × 100) и меньше 3000 (3 × 1000). Включая три цифры, частное содержит сотни, десятки и единицы. В данном случае разбиваем деление на три отдельных действия, то есть отыскиваем последовательно сотни, потом десятки и, наконец, единицы частного. Самое действие начинаем с сотен.
Отыскиваем сотни частного. Цифра сотен частного может происходить от деления сотен делимого на делитель 3. Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.
Отыскиваем единицы частного. Разделив 12 на 3, находим для единиц частного 4. Умножая 4 на 3 и вычитая произведение 12, получаем в остатке 0.
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, деление изобразится письменно:
Сносим 3 — следующую цифру делимого; 3 в 13 содержится 4 раза, 3-жды 4 составляет 12; вычитая 12 из 13, получаем в остатке 1.
Сносим 2 следующую цифру делимого; 3 в 12 содержится 4 раза, пишем в частном 4; 3-жды 4 составляет 12. Вычитая 12, получаем в остатке нуль и в частном 244.
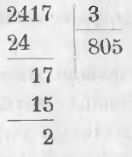
Пример. Разделить 2417 на 3. Ход вычисления выразится письменно:
Деление многозначного числа на многозначное
При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.
Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:
Определяем сотни частного:
Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.
Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.
Определяем десятки частного:
Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.
Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.
Определяем единицы частного:
47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.
Итак, после деления имеем в целом частном 791 и в остатке 30.
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:
Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.
К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.
Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.
Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.
Пример. Разделить 671064 на 335. Деление изобразится письменно:
Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.
Из предложенных примеров выводим следующее правило:
Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.
К остатку сносят следующую цифру делимого и снова задаются.
Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.
Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.
Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.
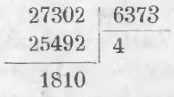
Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя. Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр. Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.
Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.
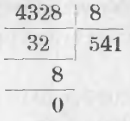
Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:
8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.
Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.
Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.
Деление на 10, 100, 1000 и т. д.
Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого. Этого мы достигаем, отделяя запятою цифру единиц. Число до запятой будет выражать частное, а после запятой — остаток.
Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:
Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.
Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.
Деление на число, оканчивающееся нулями
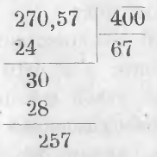
Разделяя число 27057 на 400 и поступая при этом по общему правилу
мы замечаем, что две последние цифры делимого не оказывают никакого влияния на частное. Они являются в остатке без всякой перемены. Откуда правило:
Если делитель оканчивается нулями, отделяют в делимом запятою от правой руки к левой столько цифр, сколько зачеркнуто нулей в делителе, и делят часть делимого до запятой на значащие цифры делителя. Отделенные цифры делимого приписывают к остатку.
В данном примере деление представится в виде
f
Если делимое и делитель оканчиваются нулями, их зачеркивают поровну в делимом, делителе и производят деление; зачеркнутые нули делимого приписывают к остатку.
Чтобы разделить 27300 на 4100, делим 273 на 41:
Частное будет 6, а остаток 2700.
Зависимость между данными и искомыми деления
При делении целых чисел мы имеем два случая: а) деление нацело, или без остатка, и б) деление с остатком.
Каждому из этих случаев соответствует особая зависимость между данными и искомыми деления.
Деление нацело или без остатка
При делении нацело
Частное равно делимому, разделенному на делитель.
Разделяя 42 на 7, имеем в частном 6; следовательно,
42 ÷ 7 = 6, или 6 = 42 ÷ 7
Делимое равно делителю, умноженному на частное.
Так как делитель и частное — два множителя, произведение которых равно делимому, то делитель равен делимому, разделенному на частное.
Деление с остатком
При делении с остатком
Делимое равно произведению делителя на целое частное, сложенное с остатком.
При делении 47 на 6, имеем в целом частном 7, в остатке 5.
Делимое 47 = 6 × 7 + 5.
Делимое без остатка делится нацело на делитель и на целое частное.
Разность делимого без остатка равна произведению делителя на целое частное, то есть эта разность при делении на делитель дает целое частное, при делении на целое частное дает делитель.