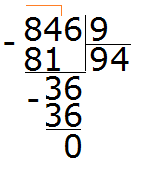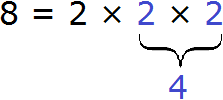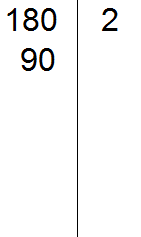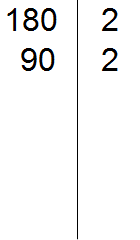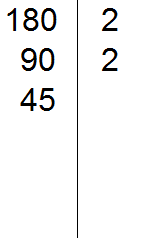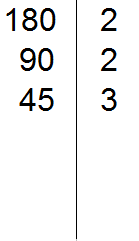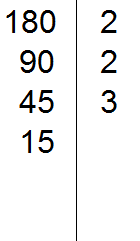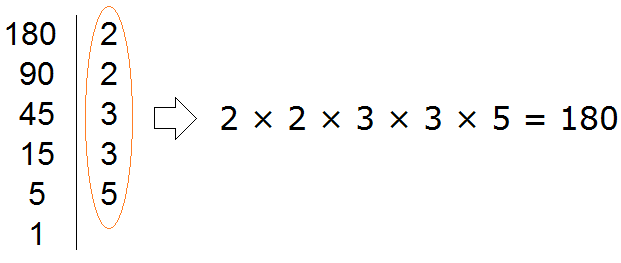Что такое делимость чисел 6 класс

Математика 6 класс. Делимость чисел

Описание презентации по отдельным слайдам:

Учитель математики: Гадаева Людмила Константиновна Математика 6 класс Муниципальное казенное общеобразовательное учреждение основная общеобразовательная школа с. Синдзикау им. А.Т.Гапбаева Дигорского района РСО-Алания

Делители и кратные Делителем натурального числа а называют натуральное число, на которое а делится без остатка. Делители 18: 1; 2; 3; 6; 9; 18 Число 1 является делителем любого натурального числа. Любое натуральное число имеет ограниченное число делителей.

Делители и кратные Кратным натуральному числу а называют натуральное число, которое делится без остатка на а. Кратные 18: 18; 36; 54; 72; 90; 108; … Любое натуральное число имеет бесконечно много кратных.

Какие из этих чисел делятся на 10? 100 3300 4005 707 90 9910 40404 10000 111

Признак делимости на 10 Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре.

Какие из этих чисел делятся на 5? 100 3555 4006 707 90 9913 40405 10000 11111

Признак делимости на 5 Если запись натурального числа оканчивается цифрами 0 или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Чётные и нечётные числа Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными. чётные 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 нечётные

100; 3555; 4008; 707; 90; 9913; 40405; 6 100; 3555; 4008; 707; 90; 9913; 40405; 6 Признак делимости на 2 Если запись натурального числа оканчивается чётной цифрой, то это число чётно (делится без остатка на 2), а если запись числа оканчивается нечётной цифрой, то это число нечётно. Выделите чётные числа:

Чётные и нечётные числа нечётное чётное нечётное чётное a b a + b чётное нечётное чётное чётное нечётное чётное нечётное нечётное

Чётные и нечётные числа нечётное чётное нечётное чётное a b a−b чётное нечётное чётное чётное нечётное чётное нечётное нечётное

1010; 3555; 40108; 7307; 927 1010; 3555; 40108; 7307; 927 Признак делимости на 9 Если сумма цифр числа делится на 9, то и число делится на 9; если сумма цифр числа не делится на 9, то и число не делится на 9. 1+0+1+0=2 – не делится на 9 3+5+5+5=18 – делится на 9 4+0+1+0+8=13 – не делится на 9 7+3+0+7=17 – не делится на 9 9+2+7=18 – делится на 9

4014; 40138; 3528; 8507; 9327 4014; 40138; 3528; 8507; 9327 Признак делимости на 3 Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3. 4+0+1+4=9 – делится на 3 3+5+2+8=18 – делится на 3 4+0+1+3+8=16 – не делится на 3 8+5+0+7=20 – не делится на 3 9+3+2+7=21 – делится на 3

1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; Простые и составные числа Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число. Натуральное число называют составным, если оно имеет более двух делителей. 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 32; 33; 34; 35; 36; …

Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычеркивали, а выкалывали иглой, то таблица в конце вычислений напоминала решето. Поэтому метод Эратосфена называют решетом Эратосфена: в этом решете «отсеиваются» простые числа от составных.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120

Источник

Признаки делимости чисел

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое «признак делимости»

Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.

Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.

Однозначные, двузначные и трехзначные числа

Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.

Трехзначные числа — числа, в составе которых три знака (три цифры).

Чётные и нечётные числа

Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!

Признаки делимости чисел

Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.

Признак делимости на 3. Сумма цифр числа должна делиться на 3.

Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.

Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.

Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.

Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.

Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.

Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Источник

Делители и кратные

В данном уроке мы рассмотрим такие понятия как делители и кратные.

Что такое делитель?

Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.

Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:

Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:

Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:

10 : 4 = 2 (2 в остатке)

Определение. Делителем числа а называется число, на которое число а делится без остатка.

Делителем числа 12 называется число, на которое 12 делится без остатка.

Попробуем перечислить эти числа:

Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:

12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1

Кратные числа

Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3

Определение. Кратным числа а называется число, которое делится без остатка на а.

Кратным числа 5 называется число, которое делится без остатка на 5 .

У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:

5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5

Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.

Признак делимости на 10

Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.

Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.

В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.

Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.

Признак делимости на 5 и на 2

Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.

Признак делимости на 5

Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.

Признак делимости на 3

Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:

Признак делимости на 9

Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9

Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:

Чётные и нечётные числа

Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:

Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:

21 : 2 = 10 (1 в остатке)

Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.

Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.

А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.

Простые и составные числа

Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:

Значит, число 5 является простым числом.

Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1

Значит, число 4 является составным числом.

Разложение составного числа на простые множители

Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.

Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.

Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4

Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6

Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.

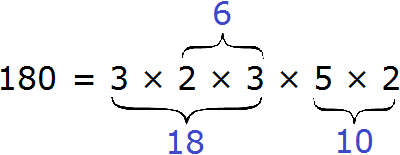
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10

Теперь раскладываем множители 18 и 10 на другие множители:

Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:

Теперь собираем все простые множители вместе:

На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.

Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.

При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.

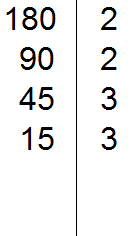
Например, разложим предыдущее число 180 этим способом.

Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.

180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:

Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.

90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:

Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.

45 на 2 не делится. Тогда проверяем делится ли 45 на 3.

45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:

Теперь делим 15. Проверяем делится ли 15 на 2.

15 не делится на 2. Тогда проверяем делится ли 15 на 3.

15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

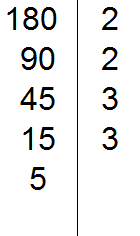
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:

Теперь делим 5. Проверяем делится ли 5 на 2.

5 не делится на 2. Тогда проверяем делится ли 5 на 3.

5 не делится на 3. Тогда проверяем делится ли 5 на 5.

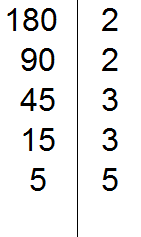
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:

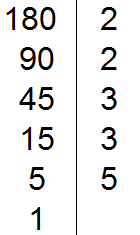
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:

На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.

Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:

Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.

Нахождение делителей числа

В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.

Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2

6 : 2 = 3

Ещё делителем числа 6 является число 3

6 : 3 = 2

Ещё делителем числа 6 является число 1

6 : 1 = 6

Наконец, делителем числа 6 является само это число

6 : 6 = 1

Перечислим все делители числа 6

1, 2, 3, 6

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.

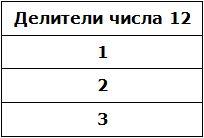
Пример 1. Найти делители числа 12

Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.

В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:

Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.

Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4

Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании приведённого примера можно сформировать правило для нахождения делителей числа:

Чтобы найти делители числа, нужно:

Пример 2. Найти делители числа 6

Первым делителем числа 6 запишем единицу:

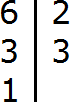
Теперь разложим число 6 на простые множители:

Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:

1, 2, 3

1, 2, 3, 6

Источник

Что такое делимость чисел 6 класс

Если натуральное число делится нацело на натуральное чис­ло , то число называют кратным числа , число — делителем числа .

1, 2, 3, 4, 6, 12 — делители 12.

Для любого натурального числа каждое из чисел

является кратным числа .

Число 6. Кратные 6 · 1, 6 · 2, 6 · 3, 6 · 4, … или по-другому запишем 6, 12, 18, 24, …

Наименьшим делителем любого натурального числа является число , а наибольшим — само число .

Число 6. Наименьший делитель: 1. Наибольший делитель: 6.

Среди чисел, кратных , наибольшего нет, а наименьшее есть — это само число .

Если каждое из чисел и делится нацело на число ,то и сумма также делится нацело на число .

+ = 12 + 6 =18 18 : 3 = 6-целое. 18 делится нацело на 3.

Если число делится нацело на число , а число не делится на­цело на число , то сумма также не делится нацело на число .

12 : 3 = 4 — целое, 7 : 3 = нецелое число. 7 не делится нацело на 3.

+ = 12 + 7 =19 19 : 3 = нецелое число. 19 не делится нацело на 3.

Простые и составные числа

Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число.

Натуральное число, имеющее более двух делителей, называют составным.

Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.

Число 6. Представим в виде произведения простых чисел: 6 = 2 · 3.

Число 8. Представим в виде произведения простых чисел: 8 = 2 · 2 · 2.

Если наибольший общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми.

Признаки делимости натуральных чисел

Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.

Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.

Если натуральное число разделить на 10, то остаток равен числу, записанному последней цифрой этого числа.

Если запись натурального числа оканчивается четной цифрой, то это число делится нацело на 2.

Если запись натурального числа оканчивается нечетной цифрой, то это число не делится нацело на 2.

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.

Если запись натурального числа оканчивается любой цифрой, отличной от цифр 0 и 5, то это число не делится нацело на 5.

Если сумма цифр натурального числа делится нацело на 9, то и само число делится нацело на 9.

Если сумма цифр натурального числа не делится нацело на 9, то и само число не делится нацело на 9.

Если сумма цифр натурального числа делится нацело на 3, то и само число делится нацело на 3.

Если сумма цифр натурального числа не делится нацело на 3, то и само число не делится нацело на 3.

Разложение числа на простые множители

Разложить числа 12 и 16 на простые множители, представить числа в виде произведения простых множителей:

12 6 3 1 2 2 3 16 8 4 2 1 2 2 2 2 12 = 2 · 2 · 3 = 2 2 · 3 16 = 2 · 2 · 2 · 2 = 2 4 ; ;

Основное свойство дроби

Если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получим дробь, равную данной:

Если числитель и знаменатель данной дроби разделить на их общий делитель (или на одно и то же натуральное число), то получим дробь, равную данной:

Сокращение дробей

Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют сокращением дроби.

3 — общий делитель чисел 9 и 24.

Дробь, числитель и знаменатель которой — взаимно простые числа, называют несократимой.

несократимая дробь, так как числа 3 и 8 взаимно простые.

Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получим несократимую дробь.

Наибольший общий делитель

Наименьшее общее кратное

Найти наименьшее общее кратное чисел 12 и 16. Разложим числа на простые множители. Выпишем разложение первого числа. Дополним числами из разложения второго числа без повторений

Другая запись : представим в виде произведения простых множителей

Приведение дробей к наименьшему общему знаменателю

Чтобы привести дроби к наименьшему общему знаменателю, надо:

1. Найти Наименьшее общее кратное чисел 24 и 36 — это число 72( 72 нацело делится и на 24, и на 36)
2. Высчитать дополнительные множители

Целые числа. Рациональные числа

Все натуральные числа, противоположные им числа и число 0 называют целыми числами.

Объединив натуральные числа с целыми отрицательными и нулем, получим целые числа.

Объединив целые числа с дробными, получим рациональные числа.

Модуль числа

Модулем числа называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.

Модуль числа обозначают так:

(читают: «модуль a»).
Модуль положительного числа равен этому числу; модуль отри­цательного числа равен числу, противоположному данному;

Модуль числа принимает только неотрицательные значения. Модули противоположных чисел равны:

Сложение и вычитание дробей

Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность двух дробей с одинаковыми знаменате­лями, надо из числителя уменьшаемого вычесть числитель вычи­таемого, а знаменатель оставить тот же.

Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а потом применить пра­вило сложения (вычитания) дробей с одинаковыми знаменателями.

Сложение и вычитание рациональных чисел

Чтобы сложить два числа с разными знаками, надо:

Чтобы сложить два отрицательных числа, надо:

Сумма двух противоположных чисел равна нулю:

— a + a = 0 и л и a — a = 0

Чтобы найти разность двух чисел можно

к уменьшаемому при­бавить число, противоположное вычитаемому.

Данная информация составлена на базе УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир. Примеры составлены мной Косыхиной Н.В.

Основные правила математики с примерами. 6 класс. Часть 1.: 2 комментария

Очень хороший сайт, помогает вспомнить школьную программу за прошлый учебный год. Спасибо создателям этого сайта, все написано в крации, без большущих текстов

Полностью согласна! Всё написано в крации. несколько раз перечитывала информацию.

Источник