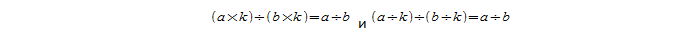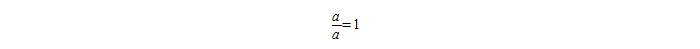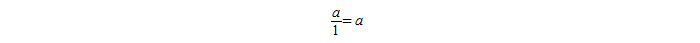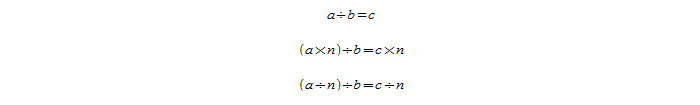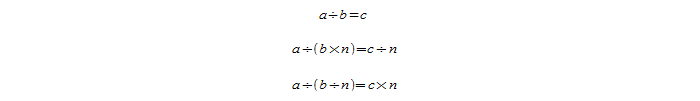Что такое делимое делитель частное 3 класс математика

Деление чисел

Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.

Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:

Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:

Для записи деления используется знак : (двоеточие), который ставится между числами. Например:

Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак = (равно), после которого записывается полученный результат:

Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?

Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.

Решение можно записать так:

Пример. Решить примеры на деление с помощью схем.

2) 12 : 4 = 3, 12: 3 = 4.

Делимое, делитель и частное

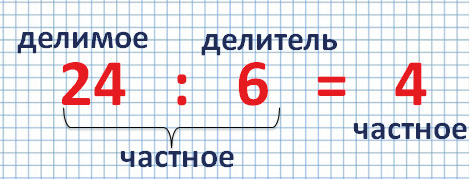
Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:

12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.

Частное — это число, которое получается в результате деления. Например, в записи:

4 — это частное. При этом сама запись 12 : 3 тоже называется частным.

Проверка деления

где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:

или умножить делитель на частное:

Источник

Деление

В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.

Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.

Как ёжикам поделить между собой яблоки поровну?

Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.

Любой пример на умножение можно представить двумя примерами на деление.

Например, для выражения 6 • 4 = 24 есть два обратных выражения:

24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.

24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.

Числа при делении

При делении, как и при другом математическом действии, каждое число имеет свое название.

Число, которое делят, называется делимое.

Число, на которое делят, называется делитель.

Результат деления называется частное.

Чтение числовых выражений

Этот пример можно прочитать по-разному.

Деление на 1

Деление на 0

Деление числа само на себя

Связь деления и умножения

Чётные и нечётные числа

Числа, которые делятся на 2 без остатка, назы­ваются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.

Чётные: 6, 22 44, 60, 74, 82, 96

Нечётные: 7, 13, 21, 37, 45, 97

В несколько раз меньше

Для примера решим задачу:

В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?

Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.

Поделись с друзьями в социальных сетях:

Источник

Деление целых чисел. Делимое, делитель, частное.

Деление целых чисел отличается от деления натуральных чисел, только тем что у целых чисел нужно у частного посчитать знак. Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.

Термины и понятия частного целых чисел.

Чтобы выполнить деление целых чисел нужно вспомнить термины и понятия. В делении есть: делимое, делитель и частное целых чисел.

Делимое – это то целое число, которое делят. Делитель – это целое число, на которое делят. Частное – это результат деления целых чисел.

Можно сказать “Деление целых чисел” или “Частное целых чисел” смысл этих фраз один и тот же, то есть нужно поделить одно целое число на другое и получить ответ.

Деление берет свое начало из умножения. Рассмотрим пример:

У нас есть два множителя 3 и 4. Но допустим нам известно, что есть один множитель 3 и результат умножения множителей их произведение 12. Как найти второй множитель? На помощь приходит деление.

Правило деления целых чисел.

Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.

Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:

Плюс на плюс дает плюс.
“+ : + = +”

Минус на минус дает плюс.
“– : – =+”

Минус на плюс дает минус.
“– : + = –”

Плюс на минус дает минус.
“+ : – = –”

А теперь рассмотрим подробно каждый пункт правила деления целых чисел.

Деление целых положительных чисел.

Вспомним, что целые положительные числа это тоже самое, что натуральные числа. Мы пользуемся теми же правила, что и при делении натуральных чисел. Знак частного от деления целых положительных чисел всегда плюс. Иными словами, при делении двух целых чисел “плюс на плюс дает плюс”.

Пример:
Выполните деление 306 на 3.

Решение:
Оба числа имеют знак “+”, поэтому ответ будет со знаком “+”.
306:3=102
Ответ: 102.

Пример:
Разделите делимое 220286 на делитель 589.

Решение:
Делимое 220286 и делитель 589 имеет знак плюс, поэтому частное тоже будет иметь знак плюс.
220286:589=374
Ответ: 374

Деление целых отрицательных чисел.

Правило деления двух отрицательных чисел.

Пусть у нас будут два отрицательных целых числа a и b. Нам нужно найти их модули и выполнить деление.

Результат деления или частное двух отрицательных целых чисел будет со знаком “+” или “минус на минус дает плюс”.

Решение:
-504:(-14)=|-504|:|-14|=504:14=34
Записать выражение можно короче:
-504:(-14)=34

Деление целых чисел с разными знаками. Правило и примеры.

При выполнении деления целых чисел с разными знаками, частное будет равно отрицательному числу.

Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.

Минус на плюс дает минус.
Плюс на минус дает минус.

Пример:
Вычислите деление 4716:(-524).

Нуль деленный на целое число. Правило.

При деление нуля на целое число ответ будет равен нулю.

Пример:
Выполните деление 0:558.

На нуль делить нельзя.

Нельзя 0 разделить на 0.

Проверка частного деления целых чисел.

Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.

Проверка результата деления краткая формула:
Делитель ∙ Частное = Делимое

Рассмотрим пример:
Выполните деление и сделайте проверку 1888:(-32).

Решение:
Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число.
1888:(-32)=-59

А теперь выполним проверку найденного ответа:
1888 – делимое,
-32 – делитель,
-59 – частное,

Делитель умножаем на частное.
-32∙(-59)=1888

Вопросы по теме:
Что такое частное чисел?
Ответ: частное чисел – это результат деления деления двух чисел.

Как найти частное?
Ответ: нужно одно число поделить на другое, то есть делимое поделить на делитель и получим частное.

Чему равно частное от деления целых чисел?
Ответ: если целые числа делятся без остатка, то их частное равно целому числу. Иначе будет дробное число.

Что такое делимое и делитель?
Ответ: число которое делят называют делимым, а число на которое делят называют делителем.

Пример:
Найдите частное суммы и разности чисел 48 и 16.

Решение:
Находим сумму чисел 48 и 16.
48+16=64
Находим разность чисел 48 и 16.
48-16=32
Находим частное.
64:32=2
Ответ: 2.

Источник

Урок математики. Тема:Делимое.Делитель( 3 класс)

Выбранный для просмотра документ 925155.ppt

Описание презентации по отдельным слайдам:

Геометрическая задача 6 см 4 см Периметр-? Решение: 6+6+4+4=20 (см)- перимерт Ответ: 20 см

Игра «Молчанка» 7 12 9 16 10 2 20 Все однозначные числа умножить на 2. Все двузначные числа разделить на 2. Проверяй-ка 14 6 18 8 5 4 10

«Знайка дня» 84 : 7= 88 : 4= 78 : 6= 85 : 5= 48 : 3= 68 : 2= 76:4= 50 : 2= КАНИКУЛЫ а к к и н у л ы 22 12 16 17 13 34 25 19

Тема: Делимое. Делитель.

Мы исследователи… 6: = 2 8 : =2 делитель = : 2 =7 : 5 = 2 делимое = 3 4 10 14 делимое:частное Частное делитель

делитель х частное = делимое делимое : частное = делитель

9 9 40 6 делимое делитель частное 72 8 63 7 5 8 42 7

Тест а) Подчеркни выражения, в которых надо найти частное. 4 + 3 5 * 2 6 : 3 8 – 4 4 > 3 12 : 2 б) В данных равенствах подчеркни делитель. 16 : 2 = 8 3 * 5 = 15 2 * 7 = 14 8 : 4 = 2 в) В данных равенствах обведи кружочком делимое. 15 : 3 = 5 3 * 2 = 6 14 : 2 = 7 9 – 4 = 5 Г ) В данных равенствах подчеркни частное чисел. 2 * 9 = 18 18 : 3 = 6 12 : 4 = 3 10 : 2 = 5 д) Подчеркни правильный ответ на вопрос:«Какое самое большое число при делении?» частное делимое делитель

Рефлексия У меня получилось … Мне нужно поработать над…..

Выбранный для просмотра документ Урок.Делимое.Делитель.doc

Урок математики в 3 классе

Раздел «Умножение и деление»

обсуждение изученного материала;

индивидуальная работа с учащимися;

самостоятельная работа;

фронтальная форма познавательной деятельности;

игровые упражнения.

Цели урока и задачи:

совершенствовать навыки нахождения делимого и делителя

конкретизировать знания учащихся по данной теме;

совершенствовать вычислительные навыки, развивать познавательный интерес, умение рассуждать

развивать и обогащать речь учащихся;

повторить изученный материал;

воспитывать любовь к предмету, аккуратность, дружеское отношение между детьми.

Источник

Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.

Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.

Основное свойство частного

Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.

По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.

Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:

10 — 2 — 2 — 2 — 2 — 2 = 0.

Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:

Частное чисел – это итог процесса деления одного значения на второе. Пример:

Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:

При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:

Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:

Увеличение или уменьшение делимого

Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.

Изложенное правило имеет такой вид:

12 ⁄ 2 = 6 и пусть n = 3.

Проведём увеличение и уменьшение делимого:

То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.

Увеличение или уменьшение делителя

Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:

Для примера требуется взять частное двух значений 54 и 6:

a / b = c и пусть n = 3.

Проведём увеличение и уменьшение делителя:

Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.

Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.

Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.

Источник