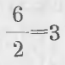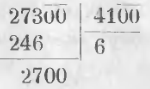Что такое деление нацело 6 класс

Презентация по математике на тему «Деление нацело»

Описание презентации по отдельным слайдам:

Описание слайда:

Математика 5 класс
08.11.2021
Тема урока
Деление нацело.
подготовила
учитель математики
Латышева И.С.

Описание слайда:

Учебные платформы: Инфоурок

Описание слайда:

У нас есть натуральные числа a и b, причём а больше b или равно b (a ≥ b). Говорят, что а делится на b нацело, если существует натуральное число с, при умножении которого на b получается a : a = b ∙ c.
Обычно слово «нацело» в этой фразе опускается. При этом записывают:
a : b = с и называют а – делимым, b – делителем, с – частным.
Любое натуральное число а делится на 1 и само на себя:
а : 1 = а, а : а = 1
так как а ∙ 1 = а, 1 ∙ а = а.
Например, 12 делится на 1 и на 12.
12 : 1 = 12, 12 : 12 = 1
При делении нуля на любое натуральное число получается нуль:
0 : а = 0, потому что 0 ∙ а = 0.
Запомните: делить на нуль нельзя!
Любое натуральное число а делить на нуль нельзя, потому что не существует такого числа с, для которого выполнялось бы равенство а : 0 = с (так как с ∙ 0 = 0 ≠ а). Принято считать, что нуль на нуль делить нельзя.

Описание слайда:

Описание слайда:

Посчитаем, сколько цифр осталось в делимом, после неполного частного. У нас после 39 стоит только одна цифра – 2. Значит, и в результат добавляем ещё одну точку.
Приступаем к делению: 28 помещается в 39 только один раз, поэтому ставим первой цифрой ответа единицу и вычитаем 28 из 39.
После вычитания в остатке получилось 11, это меньше, чем 28, поэтому к 11 дописываем 2.

Описание слайда:

112 делится на 28. Получаем 4. Записываем полученный результат второй цифрой в ответе.
В остатке получился нуль – значит, числа разделились нацело. Таким образом, 392 : 28 = 14.

Описание слайда:

Описание слайда:

Вычислим выражение: 128 : 4 + 40 : 4.
Рассмотрим два способа решения.
1 способ. Выполним деление и сложим результаты.
128 : 4 + 40 : 4 = 32 + 10 = 42
2 способ. Заметим, что у нас есть общий делитель – 4. Вынесем его за скобки. Получим:
(128 + 40) : 4 = 168 : 4 = 42.
В обоих случаях у нас получился один и тот же ответ. Значит, свойство верно.

Описание слайда:

Домашнее задание
Стр 41 –выучить правила
Стр 41-182,183
Стр 42-187

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Урок на тему: «Деление нацело» 6 класс

Цель. Продолжить формировать навыки деления натуральных чисел нацело. Рассмотреть свойство частного.

Проверка домашнего задания.

Актуализация опорных знаний.

1. Что называют степенью числа а с натуральным показателем n? Основание степени? Показатель степени?

2. Чему равно 1 в степени п?

3. Чему равно а в степени 1?

4. Чему равно 0 в степени п?

5. Какой порядок выполнения действий в выражении, содержащим степени?

1) ; 2) .

1) ; 1) ;

2) ; 2) 324 : 36 = 9;

3) 16 + 49 = 65. 3) ;

Объяснение нового материала.

В начальной школе вместе с действием умножения вы изучали и другое арифметическое действие второй ступени — деление.

Как называются компоненты при делении? (число, которое делят, называется делимым, а то, на которое делят, — делителем. Результат действия деления называется частным).

Умножение и деление — взаимно обратные действия. Именно поэтому умножение проверяют делением, а деление — умножением.

Пусть а и b – натуральные числа и .

Определение. а делится на b нацело, если существует натуральное число с, при умножении которого на b получается а.

? Всегда ли одно натуральное число можно разделить на другое нацело? Не всегда. Например, частное 5 : 3 невозможно выразить натуральным числом.

Любое натуральное число а делится на 1 и само на себя:

1) произведение двух натуральных чисел всегда является натуральным числом;

2) частное двух натуральных чисел не всегда можно выразить натуральным числом;

на 0 делить нельзя.

Свойство. Делимое и делитель можно умножить или разделить нацело на одно и то же натуральное число – частное от этого не изменится.

Пример 1. Использование свойства частного: 48 : 8.

2) (48 2) : (8 2) = 96 : 16 = 6;

3) (48 : 4) : (8 : 4) = 12 : 2 = 6.

Пример 2. Вычислите, используя свойство частного:

1) 3 600 : 400 = (3 600 : 100) : (400 : 100) = 36 : 4 = 9;

2) 2 500 : 50 = (2 500 : 10) : (50 : 10) = 250 : 5 = 50.

Обратите внимание: с помощью действия деления:

по известному произведению и одному из множителей находят второй множитель;

данное число уменьшают в указанное количество раз;

выясняют, во сколько раз одно число больше второго или меньше его.

Уч.с.42 № 179(Устно). Объясните почему верно равенство:

а) (42 : 6) 6 = 42; а) (625 : 25) 25 = 625.

Уч.с.42 № 180(1ст.). Заполните пропуски:

а) , ;

в) , .

Уч.с.42 № 182(д,ж,з). Запишите следующее число в виде произведения двух множителей различными способами:

д) 27 = 1 27, ж) 16 = 1 16, з) 24 = 1 24,

27 = 3 9; 16 = 2 8, 24 = 2 12,

Уч.с.42 № 184(1ст.). Найдите частное чисел:

а) 40 : 8 = 5; г) 560 : 7 = 80; ж) 606 : 2 = 303.

Уч.с.42 № 185(1ст.). Вычислите частное по образцу:

а) 400 : 80 = (400 : 10) : (80 : 10) = 40 : 8 = 5; (образец)

б) 800 : 400 = (800 : 100) : (400 : 100) = 8 : 4 = 2;

д) 6400 : 1600 = (6400 : 100) : (1600 : 100) = 64 : 16 = 4.

Подведение итогов урока.

1. Назовите компоненты действия деления. Как называется результат действия деления? Можно ли найти результат деления, если делимое равно 0? Делитель равен 0?

2. Что будет результатом деления, если делитель равен делимому?

3. Что будет результатом деления, если делитель равен 1?
4. Сформулируйте свойство частного.

Домашнее задание. § 1.12 (выучить теорию) 180(2ст.), 182(а-г), 184(2ст.), 185(2ст.).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

География: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1417000

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Итоговое сочинение успешно написали более 97% выпускников школ

Время чтения: 2 минуты

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

В России стартует пилотный проект по реабилитации детей-инвалидов

Время чтения: 2 минуты

В Липецкой области начинающие педагоги получат 120 тысяч рублей

Время чтения: 0 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Деление рациональных чисел (6 класс, математика) – правило

Что такое деление?

Первое, что необходимо узнать в теме деление рациональных чисел – это что такое деление. Деление – это операция обратная умножению. Деление подразумевает под собой, что в результате вычисления мы должны узнать, сколько раз в делимом поместился делитель. Иначе говоря, сколько раз нужно сложить делитель с самим собой, чтобы получить делимое. Или же на какое число нужно умножить делимое, чтобы получить делитель. Именно последнее определение чаще всего используется в современных учебниках математики.

Деление нацело

Деление нацело – это деление без остатка. Для того, что овладеть этим подвидом деления, для начала, нужно наизусть выучить таблицу умножения. Математика редко требует слепого заучивания, но это один из этих случаев. После этого простейшие примеры деления нацело станут, действительно, простейшими. Приведем пример.

$6*7=42$ – это один из столбцов таблицы умножения. Соответственно:

$42:7=6$ – вот соответствующая этой строке процедура деления. Более большие числа делятся в столбик.

Деление с остатком

Деление нацело подразумевает деление без остатка. Деление с остатком также имеет место быть. Это процедура, которая регулярно выполнятся во множестве самых обычных продуктовых магазинов при подсчете сдачи от покупки.

Для того, чтобы разделить одно число на другое с остатком придется подобрать число, меньше делимого, которое делиться на делитель с остатком. Результат деления этого числа на делитель и будет результатом деления, а остаток это разность изначального делимого и найденного. Приведем пример:

$53:5$ – ближайшее число, которое меньше, чем 53 и делится на 5 это 50.

$50:5=10$ – это результат.

$53-50=3$ – это остаток. Теперь запишем выражение полностью без промежуточных вычислений:

Деление дробных чисел

Числа бывают как целые, так и дробные. Причем последние также могут подвергаться процедуре деления. Рациональные дроби делятся с помощью переворачивания делителя.

Дробь делитель преображается так, что числитель становится знаменателем, а знаменатель числителем. Деление изначальных чисел будет равняться умножению делимого на перевернутую дробь.

Таким же способом можно делить и десятичные дроби после преобразования их в натуральные.

Десятичные дроби делятся с помощью перенесения запятой. Делимое и делитель домножаются на 10 в такой степени, чтобы оба числа стали целыми.

Домножить необходимо на одинаковое число, чтобы не нарушить тождество выражения.

Правило деления рациональных чисел распространяется как на целые, так и на дробные числа..

Что мы узнали?

Мы рассмотрели все виды деления, привели общие принципы и приемы, которые применяют для правильного выполнения этой операции.

Источник

Признаки делимости чисел

В данной публикации мы рассмотрим признаки делимости на числа от 2 до 11, сопроводив их примерами для лучшего понимания.

Признак делимости – это алгоритм, используя который можно сравнительно быстро определить, является ли рассматриваемое число кратным заранее заданному (т.е. делится ли на него без остатка).

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два.

Примеры:

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три.

Примеры:

Признак делимости на 4

Двузначное число

Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.

Число разрядов больше 2

Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.

Примечание:

Число делится на 4 без остатка, если:

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5.

Примеры:

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем (см. признаки выше).

Примеры:

Признак делимости на 7

Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.

Признак делимости на 8

Трехзначное число

Число делится на 8 тогда и только тогда, когда сумма цифры в разряде единиц, удвоенной цифры в разряде десятков и учетверенной в разряде сотен делится на восемь.

Число разрядов больше 3

Число делится на 8, когда три последние цифры образуют число, делящееся на 8.

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.

Примеры:

Признак делимости на 10

Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Примеры:

Признак делимости на 11

Число делится на 11 тогда и только тогда, когда модуль разности сумм четных и нечетных разрядов равен нулю или делится на одиннадцать.

Примеры:

Источник

Математика

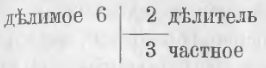
Определить, сколько раз нужно взять слагаемым меньшее число 2, чтобы получить большее число 6, значит определить, сколько раз число 2 содержится в 6, или сколько раз число 6 содержит 2.

Число 2 содержится в 6 три раза, ибо, чтобы получить 6, нужно взять сумму трех равных слагаемых:

Найти, сколько раз число 2 содержится в 6, значит разделить 6 на 2.

Определение. Деление есть такое действие, в котором по двум данным числам определяют, сколько раз одно число содержится в другом.

Данные числа в делении называются делимым и делителем, искомое называется частным.

Делимое есть то число, которое содержит другое.

Делитель есть то число, которое содержится в другом.

Частное показывает, сколько раз делитель содержится в делимом.

В данном примере делимое есть 6, делитель 2, частное 3.

Разделить 6 на 2 значит также разбить 6 на 2 равных слагаемых и отыскать их величину. Число 6 представится при помощи двух равных слагаемых в виде:

Каждое из равных слагаемых называется частью делимого.

Посредством деления целых чисел также узнается, как велико каждое слагаемое, если делимое разобьется на столько равных слагаемых, сколько в делителе единиц.

В этом случае делимое есть то число, которое делится или разбивается на равные части. Делитель показывает, на сколько равных частей делится делимое. Частное показывает, сколько приходится на каждую часть.

Способы деления

Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.

С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:

следовательно, 4 содержится в 12 три раза.

С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:

Отсюда находим, что можно вычесть 4 из 12 ровно три раза.

Деление есть сокращенное вычитание равных вычитаемых.

Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.

Различные случаи при делении

При делении целых чисел бывают два случая:

Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что деление совершилось нацело или без остатка. Умножив частное 3 на делитель 4, получаем делимое 12.

Разделяя 26 на 8, мы при последовательном вычитании получаем:

Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют остатком.

Остаток всегда меньше делителя. В этом случае говорят, что деление не совершается нацело или деление совершается с остатком.

Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.

Целое частное иногда называют просто частным.

Итак, при делении мы имеем два случая:

Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.

Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.

Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.

При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому деление есть действие, обратное умножению.

Знак деления

Действие деления изображается знаком двоеточия ÷, который ставится между делимым и делителем.

Деление числа 6 на 2 изображают письменно:

Действие деления обозначается также начертанием |–, где вертикальная черта отделяет делимое, а горизонтальная делитель от частного.

В данном примере имеем:

В нашем примере деление изображается письменно:

Знак деления прешел к нам от древних математиков.

Основные приемы при делении

Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.

Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.

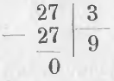
Чтобы разделить 27 на 3 мы пишем

Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое. Чтобы найти цифру частного, мы пробуем умножать делитель на разные числа или, как обыкновенно говорят, задаемся разными числами, и сравниваем произвдение делителя на частное с делимым.

Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.

Само вычисление выражают письменно:

Деление совершилось нацело.

Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.

Отыскивая целое частно, мы имеем при этом три случая:

Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:

в остатке число 7 больше делителя 4. Это показывает, что частное 5 мало и его нужно увеличить.

Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.

Взяв для частного 6, мы ход вычисления выражаем письменно:

словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:

Правило определения частного:

Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.

Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.

Если остаток меньше делителя, цифра частного верна.

Это правило показывает, что при делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя. Задаваться так, значит задаваться наибольшим целым числом.

В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и

27 = 4 × 6 + 3 = 24 + 3

Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.

Деление многозначного числа на однозначное

Частное от деления многозначного числа на однозначное иногда выражается числом, состоящим также из нескольких цифр. В этом случае деление распадается на несколько отдельных действий.

Разделим 702 на 3. Частное содержит три цифры. Оно больше 100 и меньше 1000, ибо делимое больше 300 (3 × 100) и меньше 3000 (3 × 1000). Включая три цифры, частное содержит сотни, десятки и единицы. В данном случае разбиваем деление на три отдельных действия, то есть отыскиваем последовательно сотни, потом десятки и, наконец, единицы частного. Самое действие начинаем с сотен.

Отыскиваем сотни частного. Цифра сотен частного может происходить от деления сотен делимого на делитель 3. Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.

Отыскиваем единицы частного. Разделив 12 на 3, находим для единиц частного 4. Умножая 4 на 3 и вычитая произведение 12, получаем в остатке 0.

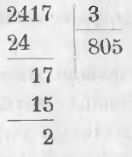
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, деление изобразится письменно:

Сносим 3 — следующую цифру делимого; 3 в 13 содержится 4 раза, 3-жды 4 составляет 12; вычитая 12 из 13, получаем в остатке 1.

Сносим 2 следующую цифру делимого; 3 в 12 содержится 4 раза, пишем в частном 4; 3-жды 4 составляет 12. Вычитая 12, получаем в остатке нуль и в частном 244.

Пример. Разделить 2417 на 3. Ход вычисления выразится письменно:

Деление многозначного числа на многозначное

При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.

Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:

Определяем сотни частного:

Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.

Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.

Определяем десятки частного:

Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.

Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.

Определяем единицы частного:

47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.

Итак, после деления имеем в целом частном 791 и в остатке 30.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:

Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.

К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.

Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.

Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.

Пример. Разделить 671064 на 335. Деление изобразится письменно:

Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.

Из предложенных примеров выводим следующее правило:

Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.

К остатку сносят следующую цифру делимого и снова задаются.

Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.

Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.

Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.

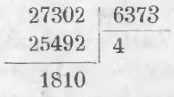
Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя. Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр. Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.

Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.

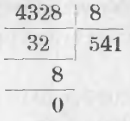
Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:

8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.

Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.

Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.

Деление на 10, 100, 1000 и т. д.

Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого. Этого мы достигаем, отделяя запятою цифру единиц. Число до запятой будет выражать частное, а после запятой — остаток.

Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:

Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.

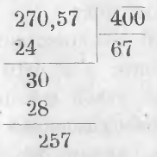
Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.

Деление на число, оканчивающееся нулями

Разделяя число 27057 на 400 и поступая при этом по общему правилу

мы замечаем, что две последние цифры делимого не оказывают никакого влияния на частное. Они являются в остатке без всякой перемены. Откуда правило:

Если делитель оканчивается нулями, отделяют в делимом запятою от правой руки к левой столько цифр, сколько зачеркнуто нулей в делителе, и делят часть делимого до запятой на значащие цифры делителя. Отделенные цифры делимого приписывают к остатку.

В данном примере деление представится в виде

f

Если делимое и делитель оканчиваются нулями, их зачеркивают поровну в делимом, делителе и производят деление; зачеркнутые нули делимого приписывают к остатку.

Чтобы разделить 27300 на 4100, делим 273 на 41:

Частное будет 6, а остаток 2700.

Зависимость между данными и искомыми деления

При делении целых чисел мы имеем два случая: а) деление нацело, или без остатка, и б) деление с остатком.

Каждому из этих случаев соответствует особая зависимость между данными и искомыми деления.

Деление нацело или без остатка

При делении нацело

Частное равно делимому, разделенному на делитель.

Разделяя 42 на 7, имеем в частном 6; следовательно,

42 ÷ 7 = 6, или 6 = 42 ÷ 7

Делимое равно делителю, умноженному на частное.

Так как делитель и частное — два множителя, произведение которых равно делимому, то делитель равен делимому, разделенному на частное.

Деление с остатком

При делении с остатком

Делимое равно произведению делителя на целое частное, сложенное с остатком.

При делении 47 на 6, имеем в целом частном 7, в остатке 5.

Делимое 47 = 6 × 7 + 5.

Делимое без остатка делится нацело на делитель и на целое частное.

Разность делимого без остатка равна произведению делителя на целое частное, то есть эта разность при делении на делитель дает целое частное, при делении на целое частное дает делитель.

Источник