Что такое декартовые координаты на числовой окружности
Прямоугольная система координат. Ось абсцисс и ординат
Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Урок «Числовая окружность на координатной плоскости»
Краткое описание документа:
Числовой окружности в 10 классе уделяется достаточно много времени. Это связано со значимостью этого математического объекта для всего курса математики.
Огромное значение для хорошего усвоения материала имеет правильная подборка средств обучения. К наиболее эффективным таким средствам относятся видеоуроки. В последнее время они достигают пика популярности. Поэтому автор не стал отставать от современности и разработал в помощь учителям математики столь замечательное пособие – видеоурок по теме «Числовая окружность на координатной плоскости».
Данный урок по длительности занимает 15:22 минут. Это практически максимальное время, которое может затратить учитель на самостоятельное объяснение материала по теме. Так как на объяснение нового материала уходит столько много времени, то на закрепление необходимо подобрать самые эффективные задания и упражнения, а также выделить еще один урок, где обучающиеся будут решать задания по данной теме.
Урок начинается с изображения числовой окружности в системе координат. Автор строит эту окружность и поясняет свои действия. Затем автор называет точки пересечения числовой окружности с осями координат. Далее поясняется, какие координаты будут иметь точки окружности в разных четвертях.
После этого автор напоминает, как выглядит уравнение окружности. И вниманию слушателей представляется два макета с изображением некоторых точек на окружности. Благодаря этому, на следующем шаге автор показывает, как находятся координаты точек окружности, соответствующие определенным числам, отмеченным на шаблонах. Так получается таблица значений переменных xи y в уравнении окружности.
Далее предлагается рассмотреть пример, где необходимо определить координаты точек окружности. Перед тем, как начинать решать пример, вводится некоторое замечание, которое помогает при решении. А затем на экране появляется полное, четко структурированное и наполненное иллюстрациями решение. Здесь также присутствуют таблицы, которые облегчают понимание сущность примера.
Затем рассматриваются еще шесть примеров, которые менее трудоемкие, чем первый, но не менее важные и отражающие главную идею урока. Здесь решения представлены в полном объеме, с подробным рассказом и с элементами наглядности. А именно, в решении присутствуют рисунки, иллюстрирующие ход решения, и математическая запись, формирующая математическую грамотность обучающихся.
Урок может быть полезен не только учителям, время которых постоянно ограничено, но и обучающимся. Особенно тем, кто получает семейное образование или занимается самообразованием. Материалами могут пользоваться те обучающиеся, которые пропустили урок по данной теме.
Тема нашего урока «ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ»
Мы уже знакомы с декартовой прямоугольной системой координат xOy ( икс о игрек). В этой системе координат расположим числовую окружность так, чтобы центр окружности был совмещен с началом координат, а ее радиус примем за масштабный отрезок.
Так как каждая точка числовой окружности имеет в системе xOy (икс о игрек) свои координаты, то для точек первой четверти икх больше нуля и игрек больше нуля;
Во-второй четверти икх меньше нуля и игрек больше нуля,
для точек третьей четверти икх меньше нуля и игрек меньше нуля,
а для четвертой четверти икх больше нуля и игрек меньше нуля
Вспомним, что уравнение окружности радиусом R c центром в начале координат имеет вид х 2 + у 2 =R 2 ( икс квадрат плюс игрек квадрат равно эр квадрат). А для единичной окружности R =1, поэтому получаем х 2 + у 2 = 1
( икс квадрат плюс игрек квадрат равно один).
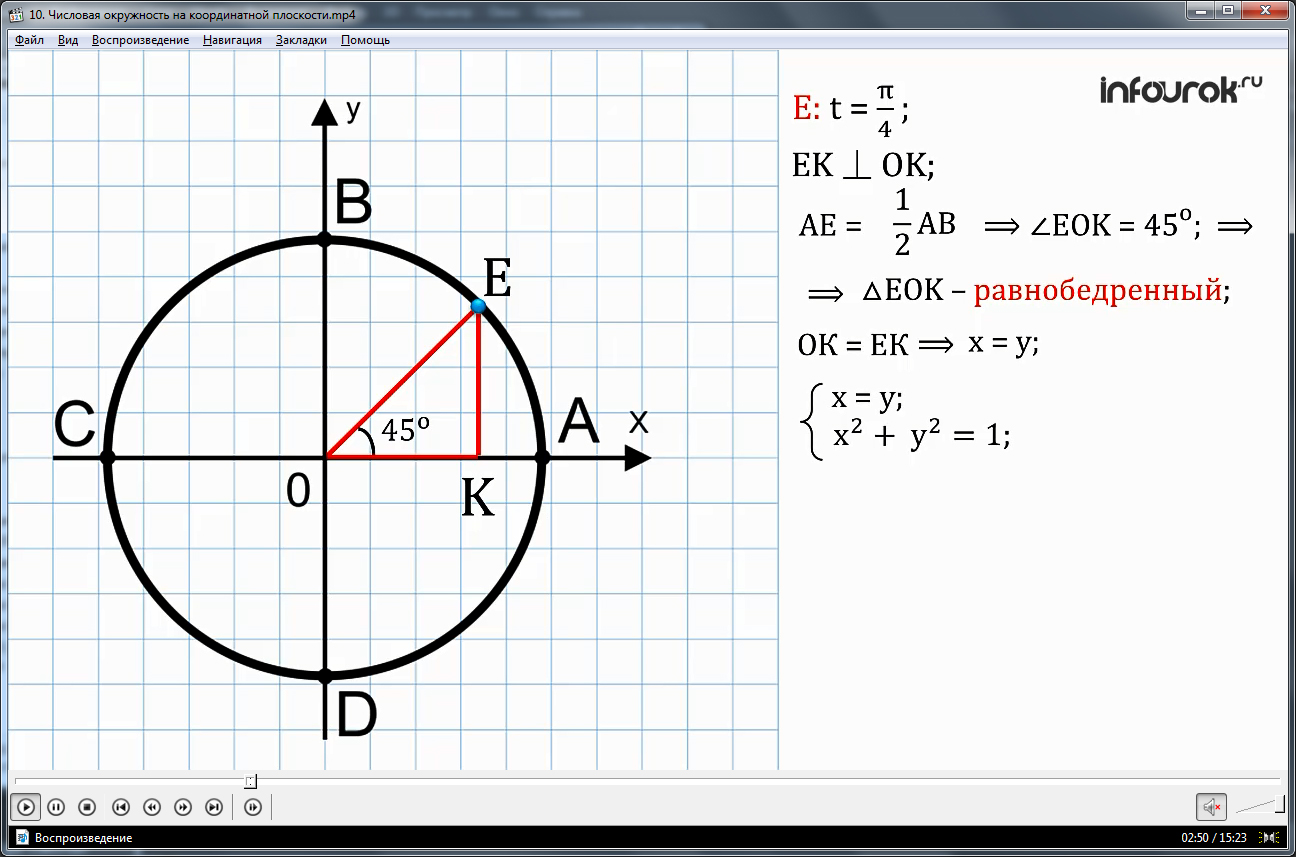
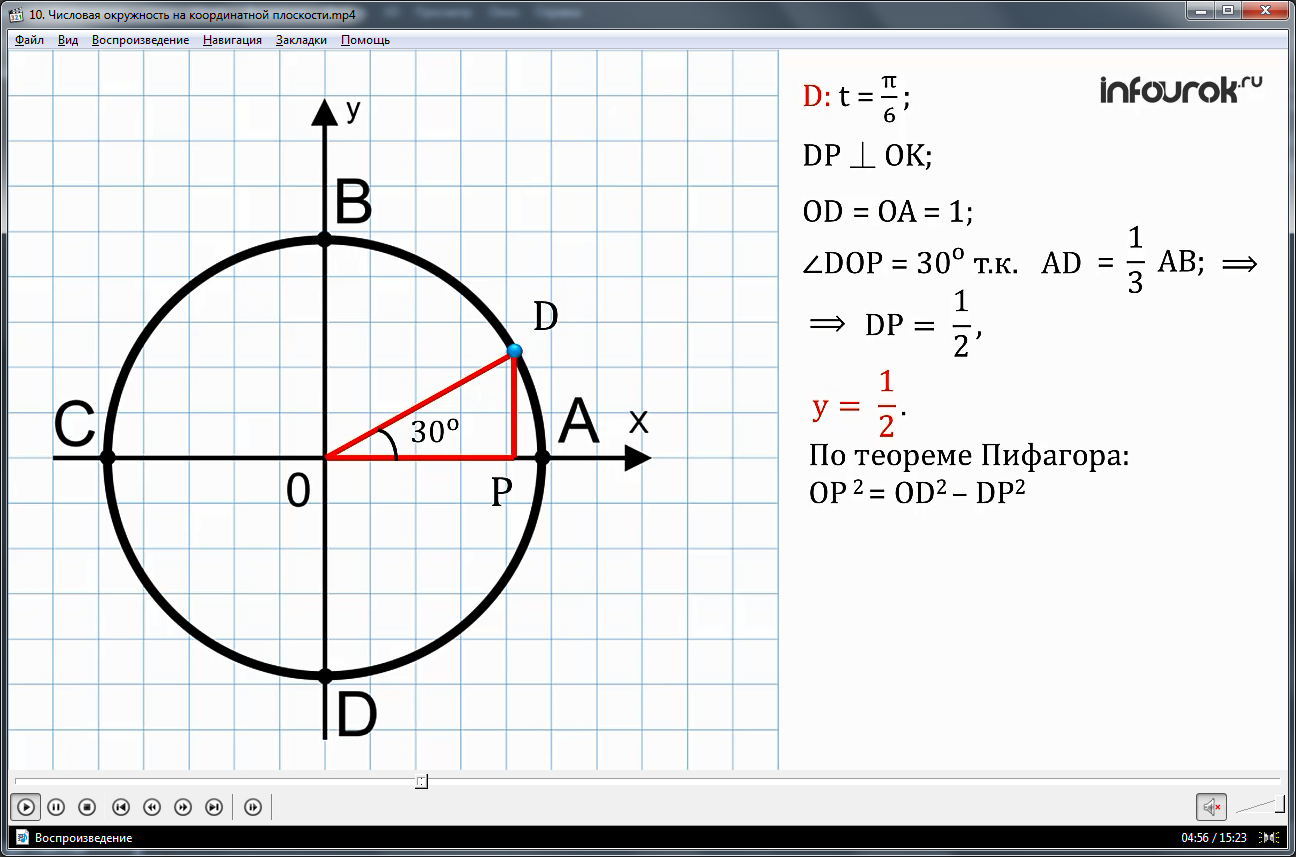
Найдем координаты точек числовой окружности, которые представлены на двух макетах (см. рис 2, 3)
Пусть точка E, которая соответствует
значит, х 2 = (икс квадрат равно трем четвертым) и х = ( икс равно корень из трех на два).
Рассуждая аналогичным образом, найдем координаты для точек, соответствующих другим числам второго макета и все полученные данные запишем в таблицы:
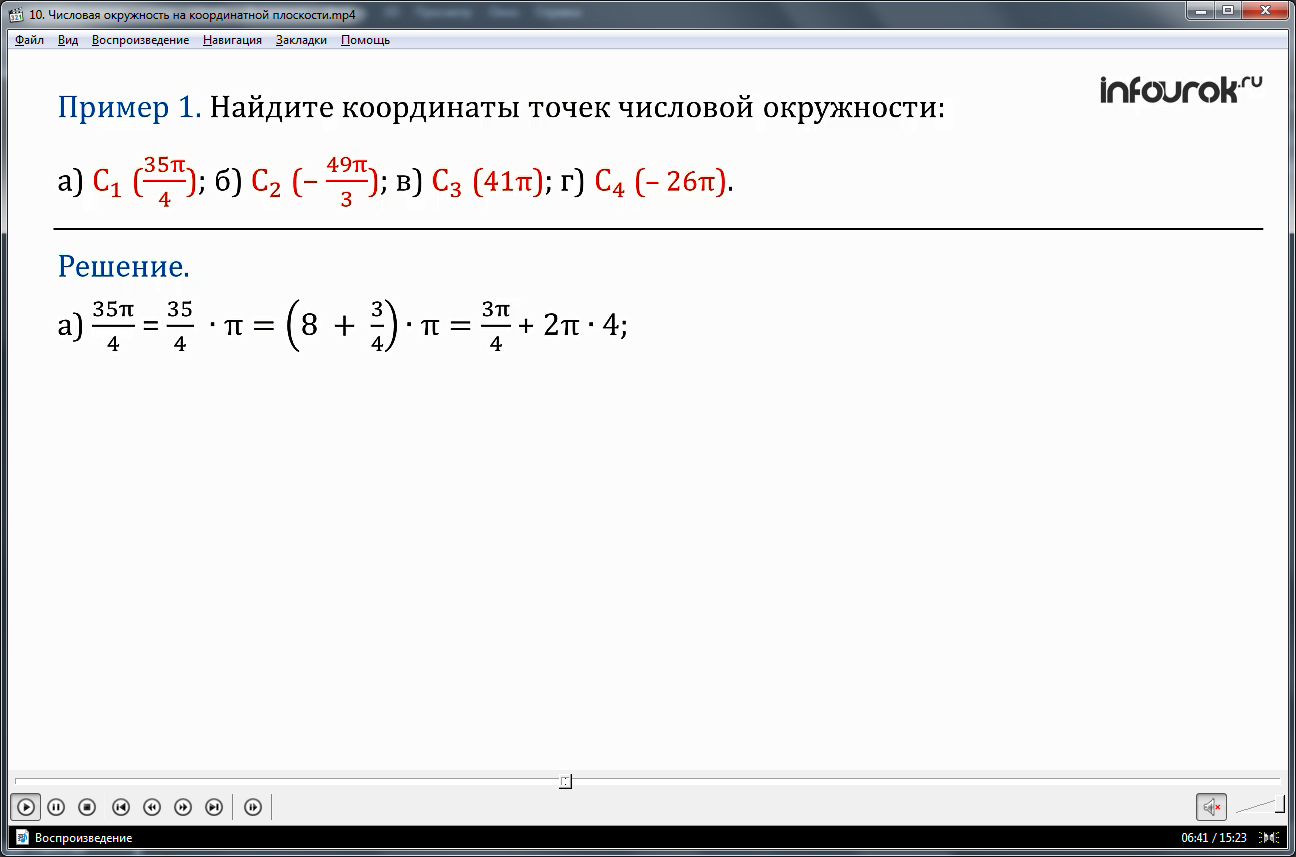
ПРИМЕР1. Найдите координаты точек числовой окружности: а) С1( );
Решение. Воспользуемся утверждение, полученным ранее: если точка D числовой окружности соответствуют числу t, то она соответствует и любому числу вида t + 2πk( тэ плюс два пи ка), где ка –любое целое число, т.е. kϵZ (ка принадлежит зэт).
ПРИМЕР 2. Найти на числовой окружности точки с ординатой у = и записать, каким числам t они соответствуют.
а любому числу все числа вида + 2πk. Часто в таких случаях говорят, что получили две серии значений : + 2πk, + 2πk.
ПРИМЕР 3. Найти на числовой окружности точки с абсциссой х = и записать, каким числам t они соответствуют.
Решение. Прямая х = пересекает числовую окружность в двух точках. Одна точка соответствует числу ( смотри второй макет),
ПРИМЕР 4. Найти на числовой окружности точки с ординатой у > и записать, каким числам t они соответствуют.
Декартовы координаты
Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.
Содержание
Прямоугольная система координат на плоскости
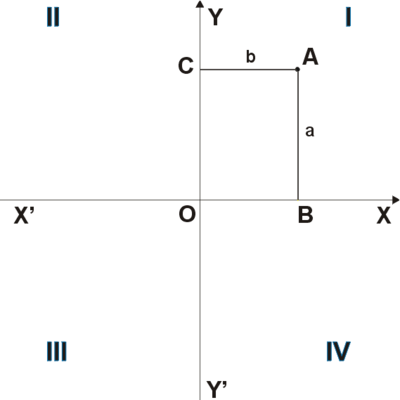
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве
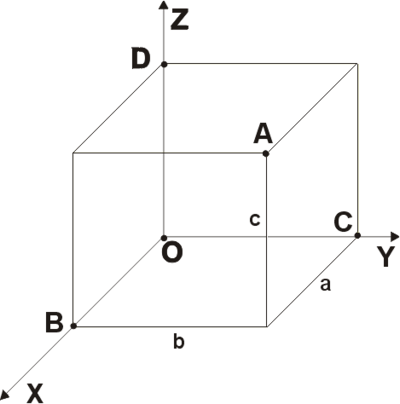
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
См. также
Ссылки
Полезное
Смотреть что такое «Декартовы координаты» в других словарях:
ДЕКАРТОВЫ КООРДИНАТЫ — (декартова система координат) система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты. Названы по имени Р. Декарта … Большой Энциклопедический словарь
декартовы координаты — Система координат, состоящая из двух перпендикулярных осей. Положение точки в такой системе формируется с помощью двух чисел, определяющих расстояние от центра координат по каждой из осей. [http://www.morepc.ru/dict/] Тематики информационные… … Справочник технического переводчика
декартовы координаты — (декартова система координат), система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты. Названы по имени Р. Декарта … Энциклопедический словарь
декартовы координаты — Dekarto koordinatės statusas T sritis Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: angl. Cartesian coordinates vok. kartesische Koordinaten, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
декартовы координаты — Dekarto koordinatės statusas T sritis fizika atitikmenys: angl. Cartesian coordinates; grid coordinates vok. kartesische Koordinaten, f rus. декартовы координаты, f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas
ДЕКАРТОВЫ КООРДИНАТЫ — способ определения положения точек на плоскости их расстояниями до двух фиксированных перпендикулярных прямых осей. Это понятие усматривается уже у Архимеда и Аппология Пергского более двух тысяч лет назад и даже у древних египтян. Впервые эта… … Математическая энциклопедия
ДЕКАРТОВЫ КООРДИНАТЫ — декартова система координат [по имени франц. философа и математика Р. Декарта (R. Descartes; 1596 1650)], система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные Д … Большой энциклопедический политехнический словарь
ДЕКАРТОВЫ КООРДИНАТЫ — (декартова система координат), система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные Д. к. Названы по имени Р. Декарта … Естествознание. Энциклопедический словарь
ДЕКАРТОВЫ КООРДИНАТЫ — Система расположения любой точки нашли кости относительно двух осей, перекрещивающихся под прямым углом. Разработанная Рене Декартом, эта система стала основой для стандартных методов графического представления данных. Горизонтальная линия… … Толковый словарь по психологии
Координаты — Координаты. На плоскости (слева) и в пространстве (справа). КООРДИНАТЫ (от латинского co совместно и ordinatus упорядоченный), числа, которые определяют положение точки на прямой, плоскости, поверхности, в пространстве. Координаты суть расстояния … Иллюстрированный энциклопедический словарь
Числовая окружность
1) Начало отсчета находится в крайней правой точке окружности;
3) Если в положительном направлении отложить на окружности расстояние \(t\), то мы попадем в точку со значением \(t\);
4) Если в отрицательном направлении отложить на окружности расстояние \(t\), то мы попадем в точку со значением \(–t\).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен \(1\). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках \(1\) и \(-1\).
Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы \(l=2πR\) мы получим:
Длина числовой окружности равна \(2π\) или примерно \(6,28\).
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте \(1\) на оси \(x\) и \(0\) на окружности – это точки на разных объектах.
Какие точки соответствуют числам \(1\), \(2\) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен \(1\)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Чтобы отметить на окружности точку соответствующую числу \(2\), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы \(3\) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: \(2π\). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа \(π\) : \( \frac<π><2>\),\(-\frac<π><2>\),\(\frac<3π><2>\), \(2π\). Поэтому при работе с окружностью чаще используют числа с \(π\). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Что надо запомнить про числовую окружность:
Декартова система координат: основные понятия и примеры
Понятие декартовой системы координат
С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.
Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.
Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.
Прямоугольная декартова система координат на плоскости
Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.
Прямоугольная декартова система координат в пространстве
Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.
Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.
Задачи о точках в декартовой системе координат
Пример 1. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось абсцисс.
Пример 2. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось ординат.
Пример 3. В декартовой системе координат на плоскости даны точки
Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения
Пример 5. В декартовой системе координат на плоскости даны точки
Продолжаем решать задачи вместе
Пример 6. В декартовой системе координат на плоскости даны точки
Пример 7. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно начала координат.
Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:
Пример 8. В декартовой системе координат в пространстве даны точки
Найти координаты проекций этих точек:
1) на плоскость Oxy ;
2) на плоскость Oxz ;
3) на плоскость Oyz ;
1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy :
2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz :
3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz :
Пример 9. В декартовой системе координат в пространстве даны точки
Найти координаты точек, симметричных этим точкам относительно:
7) начала координат.
По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.
4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:
5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:
6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:
7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат: