Что такое декартовы координаты заданной точки на окружности

Как найти координаты точки?

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

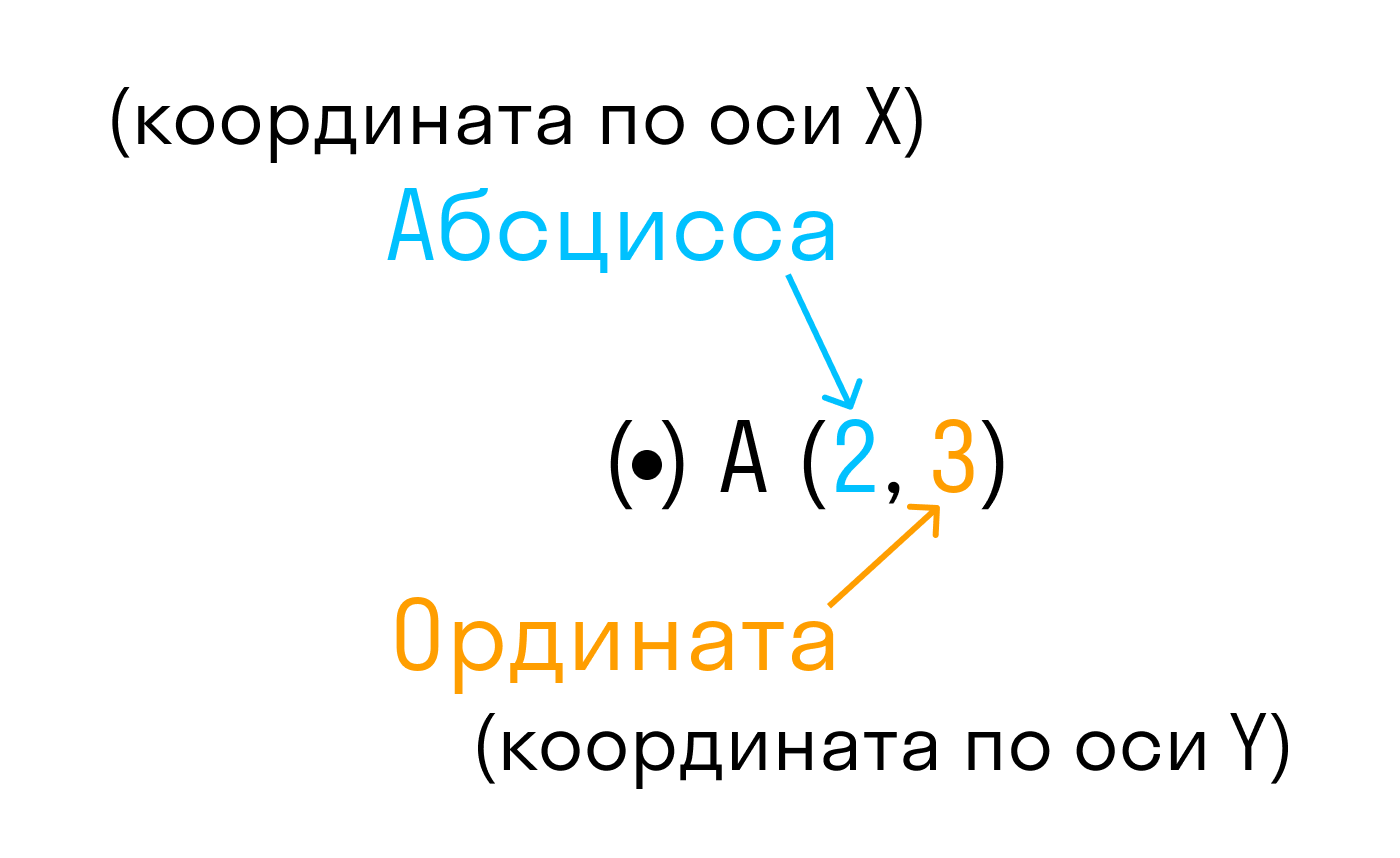
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

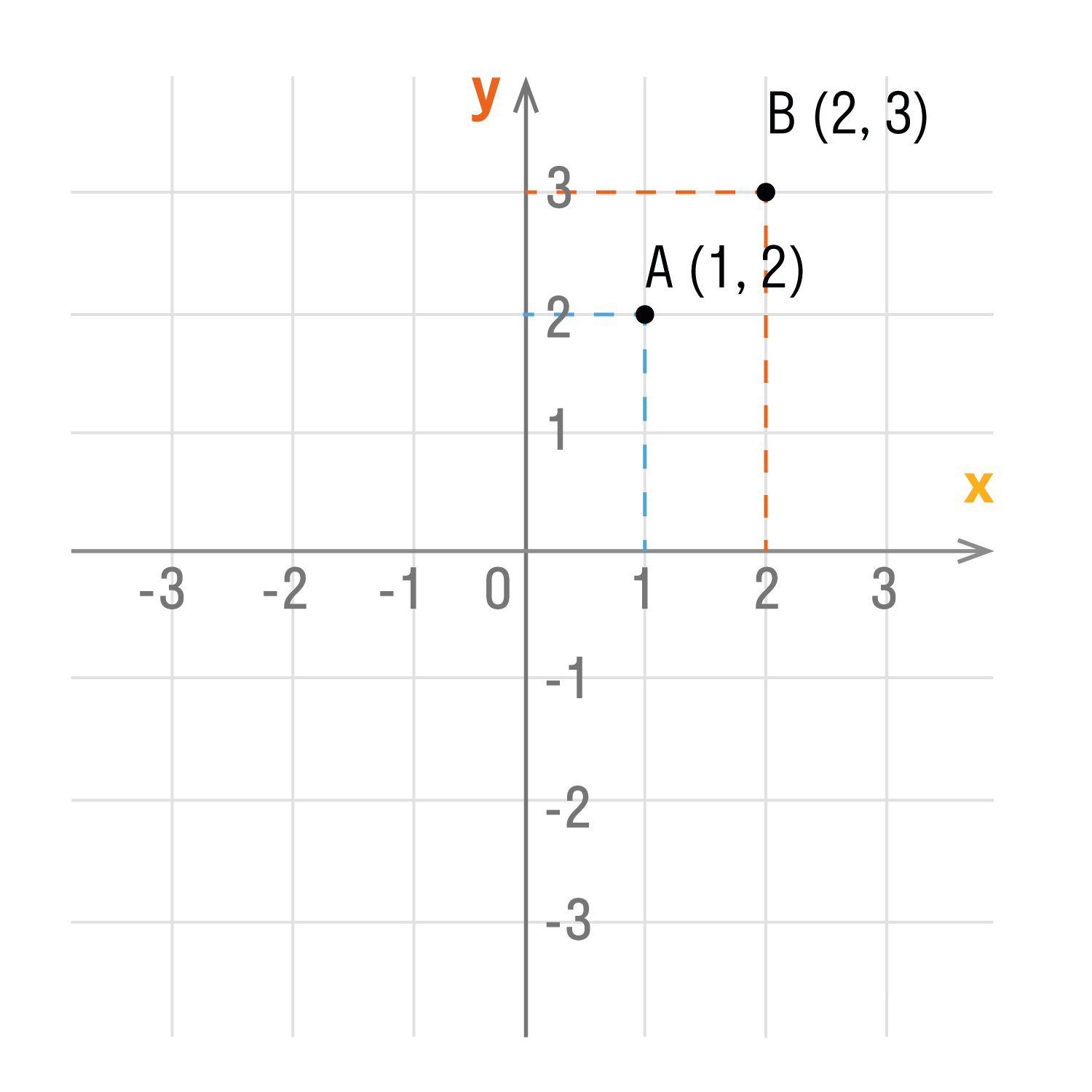
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Способ второй. Как определить положение точки D (-4, 2):

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Источник

Декартова система координат: основные понятия и примеры

Понятие декартовой системы координат

С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.

Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.

Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.

Прямоугольная декартова система координат на плоскости

Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.

Прямоугольная декартова система координат в пространстве

Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.

Задачи о точках в декартовой системе координат

Пример 1. В декартовой системе координат на плоскости даны точки

Найти координаты проекций этих точек на ось абсцисс.

Пример 2. В декартовой системе координат на плоскости даны точки

Найти координаты проекций этих точек на ось ординат.

Пример 3. В декартовой системе координат на плоскости даны точки

Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения

Пример 5. В декартовой системе координат на плоскости даны точки

Продолжаем решать задачи вместе

Пример 6. В декартовой системе координат на плоскости даны точки

Пример 7. В декартовой системе координат на плоскости даны точки

Найти координаты точек, симметричных этим точкам относительно начала координат.

Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:

Пример 8. В декартовой системе координат в пространстве даны точки

Найти координаты проекций этих точек:

1) на плоскость Oxy ;

2) на плоскость Oxz ;

3) на плоскость Oyz ;

1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy :

2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz :

3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz :

Пример 9. В декартовой системе координат в пространстве даны точки

Найти координаты точек, симметричных этим точкам относительно:

7) начала координат.

По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.

4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:

5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:

6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:

7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат:

Источник

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Источник

Декартовы координаты на плоскости и в пространстве

Декартовы координаты — это (декартова система координат) система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты.

Содержание:

Декартовы координаты на прямой

В курсе алгебры постоянно приходится пользоваться прямоугольной системой координат. Рассмотрим прямоугольную систему координат на прямой. Хорошей иллюстрацией этой системы координат является термометр.

Стрелка показывает положительное направление отсчета координат. Прямую с установленной на ней системой координат называют координатной прямой. Точку О называют началом координат. Кроме этого, на координатной прямой вводится единичный отрезок ОЕ, его иногда называют масштабом.

Декартовы координаты на плоскости

Положение точки на плоскости может быть определено ее расстоянием до двух фиксированных взаимно перпендикулярных прямых — осей. В этом случае каждой точке плоскости будет соответствовать не одно число, а пара чисел. Соответствие между точками и парами чисел задается на плоскости: выбирают прямую, называемую осью Ох, вводят на ней систему координат. На оси Ох рисуют стрелку, чтобы указать ее положительное направление. Эта ось называется также осью абсцисс.

Проводят прямую Оу, перпендикулярную оси Ох и проходящую через точку О прямой Ох, имеющую координату 0, и вводят на прямой Оу систему координат так, чтобы точка с координатой 0 совпадала с точкой О. Прямая Оу называется осью Оу или осью ординат. Положительное направление на оси Оу также указывается стрелкой. Точка О пересечения прямых Ох и Оу (осей координат) называется началом координат (рис. 2.445).

На рисунке 2.446 изображена построенная прямоугольная система координат. Если дана точка Р, то из нее опускают перпендикуляр на ось Ох. Пусть основанием перпендикуляра будет точка М и х — координата точки М на прямой Ох (рис. 2.446). Тогда число х называют абсциссой точки Р. На рисунке 2.446 .

Затем опускают из точки Р перпендикуляр на ось Оу. Пусть основанием этого перпендикуляра будет точка N и у — координата точки N на прямой Оу. Тогда число у называют ординатой точки Р. На рисунке 2.446 . Для краткости указываем, что точка Р имеет координаты х и у, так: Р(х, у). В нашем случае .

Порядок, в котором записываются координаты точки, очень существенен. Координаты (1, 3) имеет точка , а координаты (3, 1) — отличная от нее точка (рис. 2.447). Нельзя сказать, где находится точка, если неизвестно, какое число в паре чисел (х, у) стоит первым.

Ниже приводится определение координат точки на плоскости.

Определение. Абсциссой точки Р называют координату основания перпендикуляра, опущенного из точки Р на ось Ох; ординатой точки Р называют координату основания перпендикуляра, опущенного из точки Р на ось Оу.

Если прямая разбивает плоскость на две полуплоскости, то две оси координат разбивают плоскость на четыре части, называемые четвертями. Четыре четверти нумеруются в порядке, изображенном на рисунке 2.448.

Таким образом, между точками плоскости и упорядоченными парами действительных чисел имеется взаимооднозначное соответствие. Такое соответствие называют прямоугольной системой координат.

Декартовы координаты в пространстве

Построим горизонтальную плоскость и введем на ней декартову систему координат хОу (рис. 2.449).

Если ввести также координатную прямую Oz, перпендикулярную плоскости хОу в точке О, то тем самым будет введена система координат в пространстве. Точка О будет началом этой системы координат.

Стрелки осей Ох, Оу и Oz на рисунках указывают положительное направление каждой оси.

В декартовой системе координат в пространстве мы имеем три оси: Ох — ось абсцисс, Оу — ось ординат, Oz — ось аппликат. Плоскости, проходящие через оси Ох и Оу, Оу и Oz, Ох и Oz — координатные плоскости. Их обозначают соответственно: ху, yz, xz (рис. 2.450). Координатные плоскости разбивают все пространство на восемь частей — октантов.

Если задана такая система координат, то каждой точке пространства можно поставить в соответствие упорядоченную тройку действительных чисел, а каждой тройке чисел — единственную точку.

На рисунке 2.452: точка Р лежит в плоскости хОу, так что ее проекция на ось Ог есть 0. Ее проекция на ось Ох совпадает с точкой, имеющей координату 2, а на ось Оу — с точкой, имеющей координату 3. Поэтому пишут Р(2, 3, 0).

Таким образом, нахождение координат точки в пространстве сводится к построению соответствующего прямоугольного параллелепипеда (иногда его воспроизводят частично, чтобы были видны координаты точки (рис. 2.453)).

Порядок записи этих трех чисел также существенен. На рисунке 2.452 изображены точки имеющие своими координатами числа 2, 3 и 0, записанные в разном порядке.

Можно иначе находить координаты точки пространства. Пусть дана точка М. Спроектируем точку М на оси Ох, Оу, Ог в точки соответственно (рис. 2.454). Координаты точек на осях сопоставляются точке М как ее координаты х, у, г. Таким образом, координатами точки в пространстве называют координаты ее проекций на оси координат.

Если есть три координаты — три числа то для них найдется соответствующая точка пространства. На рисунке 2.455 три числа на осях координат отмечены тремя точками Пусть отрезки — ребра прямоугольного параллелепипеда с вершиной в точке О (рис. 2.456). Получили точку Р с координатами —

Прямоугольная система координат носит имя Рене Декарта (1596—1650). В 1637 г. вышла книга с длинным по обычаю времен названием «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках. Кроме того, Диоптрика, Метеоры и Геометрия, которые являются приложениями этого метода», с ней в науку вошел метод координат. Со времен Декарта алгебра и геометрия стали сотрудничать между собой к выгоде обеих дисциплин. Введенную систему координат с тех пор стали называть декартовой.

Координаты середины отрезка

Рассмотрим отрезок , принадлежащий оси Ох. Пусть Р — середина этого отрезка и пусть наши три точки имеют соответственно координаты (рис. 2.457). Выразим х через и .

1. (дано) (рис. 2.457).

2. (запись отрезка в координатах на прямой).

3. (1, 2).

Эта формула годится и в случае, когда

Рассмотрим случай, когда отрезок произвольно расположен на плоскости (рис. 2.458).

1. Точка Р является серединой отрезка (дано) (рис. 2.458).

2. Построим проекции точек на ось Ох, получим точки (построение).

3. Точка М является серединой отрезка .

4. (3, формула середины отрезка на прямой).

Аналогично можно получить, что . Все это можно сформулировать в виде теоремы.

Теорема 1. Даны точки Серединой отрезка является точка

Формула расстояния между точками

Пусть мы знаем координаты двух точек на плоскости (рис. 2.459). Имеет место следующая теорема.

Теорема 2. Расстояние между точками находится по формуле

Например, если то из полученной формулы следует, что

Формула расстояния между точками верна и в пространстве. Пусть даны две точки и Расстояние между точками Р и Q находится по формуле

Пример:

Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от его вершин.

Решение:

Из условия задачи имеем:

1. , его стороны обозначим через

3. CD = AD (требуется доказать).

Мы хотим применить для решения задачи декартову систему координат, а значит, надо удачно выбрать расположение этой системы.

4. Для данной задачи удачный выбор системы координат показан на рисунке 2.460. Начало координат помещено в точку А, а оси проведены через точки Б и С так, чтобы эти точки лежали на положительных лучах осей (построение).

5. Точка В имеет координаты (, 0), точка С — (0, ) (1, 4).

6. Середина отрезка СВ точка D имеет координаты (1, формула середины отрезка).

7. (4, 6 формула расстояния между точками).

8. (5, 6, формула расстояния между точками).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник