Что такое декартово умножение множеств

Декартово произведение множеств

В начальных классах ученики решают задачу: используя цифры 1, 2, 3 образовать всевозможные двузначные числа.

Путем перебора дети получают:

Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.

В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (а; b), образованные из элементов а и b. Это (1; 2), (1; 3), (1; 4) и т.д. Первый элемент а называют первой координатой пары, элемент b – второй.

Значит, в нашей задаче мы оперировали множеством А=<1, 2, 3> и образовывали всевозможные пары.

Рассмотрим другой пример. Пусть А=<1, 2, 3>, B=<4, 5>. Образуем всевозможные пары (а;b) так, что аА, bВ. Получим некоторое новое множество <(1; 5), (1; 4), (2; 4), (2; 5), (3; 4), (3; 5)>, элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств А и В.

Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают АВ. Таким образом АВ = <(x;y)| xA, yB>.

Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.

Количество пар в декартовом прoизведении АВ будет равно произведению числа элементов множества А и числа элементов множества В: n(АВ)=n(A)n(B).

В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.

Используя понятие кортежа, можно определить понятие декартового произведения n множеств.

Декартовым произведением множеств А, А,…, A называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А, вторая – А, …, n-ая – множеству А: АА…A.

Пусть даны множества А=<2, 3>; А=<3, 4, 5>; A=<7, 8>. Декартово произведение ААА=< (2, 3, 7), (2, 3, 8), (2, 4, 7), (2, 4, 8), (2, 5, 7),
(2, 5, 8),(3, 3, 7), (3, 4, 7), (3, 3, 8), (3, 4, 8), (3, 5, 7), (3, 5, 8)>.

Источник

Декартово (прямое) произведение множеств

ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ. СООТВЕТСТВИЯ, ФУНКЦИИ, ОТНОШЕНИЯ

ЦЕЛЬ ЛЕКЦИИ – изучение свойств декартова произведения множеств, и связанных с ним соответствий, функций и отношений.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Помимо рассмотренных в первой лекции традиционных операций над множествами существуют и другие действия с множествами, которые позволяют решать много задач, имеющих практическое применение. В частности, к таким действиям относится декартово (прямое) произведение множеств. Свое название декартово произведение получило оттого, что предложенное Декартом координатное представление точек плоскости, являлось исторически первым примером прямого произведения.

Декартово (прямое) произведение множеств

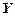
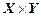
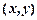
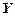
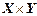
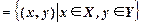
Декартово (прямое) произведение множеств Х и – это множество, обозначаемое , элементами которого являются упорядоченные пары , первая компонента которых принадлежит множеству Х, а вторая множеству .

.

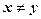
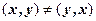
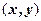
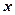
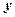
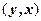
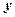
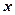
Согласно определению элементами прямого произведения множеств являются упорядоченные пары, составленные из элементов исходных множеств. В этих парах первый элемент (компонента) всегда принадлежит первому множеству, а второй элемент (компонента) второму. Порядок множеств определяется исходной записью и, если , то , так как в упорядоченной паре компонента имеет номер 1, а компонента – номер 2, но в упорядоченной паре : – номер 1, а – номер 2.

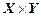
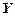
Множество содержит mn элементов, где m и n – количество элементов Хи соответственно.

Геометрическое представление этого множества приведено на рис. 2.1, а.

Пример 2.2. Пусть A и B – отрезки вещественной оси. Прямое произведение изобразится заштрихованным прямоугольником, показанным на рис. 2.1, б.

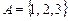
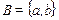
Пример 2.3. Найти декартово произведение множеств и .

Решение. A × B .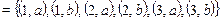

Порядок перечисления элементов безразличен, важен только порядок элементов в паре (упорядоченная пара).

B × A .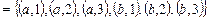

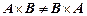
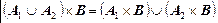
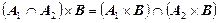
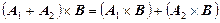
Из приведенных примеров видно, что свойства прямого произведения отличаются от свойств обычного произведения в арифметическом смысле. В частности, прямое произведение изменяется при изменении порядка сомножителей, то есть , следовательно, декартово произведение не коммутативно. При этом он не только не коммутативно, но и не ассоциативно, но дистрибутивно относительно объединения, пересечения и симметрической разности множеств

;

;

.

Прямое произведение множеств – операция многоместная

.

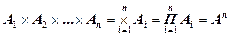
В результате получаются множества, состоящие из упорядоченной последовательности вида

, где ; ;…; .

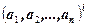
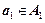
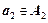
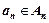
Такие последовательности называются кортежами или векторами.

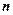
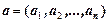
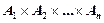
Кортеж длины – конечная последовательность элементов , в которой каждый элемент занимает определенное место в соответствии с записью исходных множеств декартова произведения.

Сами элементы при этом называются компонентами (координатами) кортежа, которые нумеруются слева направо (первая компонента, вторая компонента и т.д.).

Примеры кортежей: множество людей, стоящих в очереди, числа, выражающие координаты точки на плоскости и т.п. Во всех этих множествах место каждого элемента является вполне определенным и не может быть произвольно изменено.

Основные отличия понятий кортежа (вектора) и множества заключаются в следующем:

1) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав;

2) в множестве все элементы различны, а в кортеже координаты могут повторяться.

Таким образом, в отличии от обычного множества в кортеже (векторе) могут быть одинаковые компоненты: два одинаковых слова в фразе, одинаковые численные значения координат точки на плоскости и т.п.

Таким образом, декартово произведение позволяет получать вектора любых размерностей. Эта операция отличается от операций объединения и пересечения тем, что в результате перемножения прямым способом получаются объекты, содержащие элементы, отличающиеся по своей природе от элементов исходных множеств.

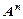
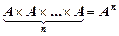
Если перемножить n раз одно и то же множество, то получится множество , называемое степенью множества

.

Степенью декартового произведения называется число множеств n, входящих в это декартово произведение.

Источник

Декартово умножение множеств

Рассмотрим следующую задачу. Сколько можно составить слогов, состоящих из двух букв, из которых первая – любая согласная из П, Р, С, а вторая – любая гласная из А, О, У, Э? Чтобы выписать все возможные слоги составим таблицу (табл. 2).

С точки зрения теории множеств из двух данных множеств
А = <П, Р, С>, В = <А, О, У, Э> образовано новое множество слогов, состоящее из пар элементов, входящих в множества А и В, причем на первом месте стоит элемент из А, а на втором – элемент из В. Множество таких пар называется декартовым (или прямым) произведением множеств А и B.

Определение. Декартовым произведением А ´ В двух множеств А и В называют множество, состоящее из всех пар элементов (а, в), таких, что а Î А, в Î В, т.е. А ´ B = <(а, в) | а Î А, в Î В>.

В частности, для любого множества А, А ´ Æ = Æ ´ А = Æ.

Операцию, при помощи которой находят декартово произведение, называют декартовым умножением множеств.

Заметим, что порядок расположения элементов в парах существенен, например, (2, 3) ≠ (3, 2).

Если A и B – числовые множества, то А ´ В – это множество упорядоченных пар чисел, изображая каждую пару чисел в прямоугольной декартовой системе координат, получим фигуру на плоскости. Например на рис. 9 изображено А ´ В множеств А = [0, 2], B = [1, 2]. На рис. 10 изображено А ´ В множеств А = <0, 1, 2>, B = [1, 2].

Так изображают графически декартово произведение двух числовых множеств.

Декартово умножение множеств не подчиняется коммутативному закону, т.е. существуют множества А и В, для которых A´В ≠ В´А. Декартово умножение не подчиняется и ассоциативному закону, но связано с операциями объединения, пересечения и вычитания множеств дистрибутивными свойствами: для любых множеств А, В и С имеют место равенства:

(А В) ´ С = (A ´ С) (В ´ С), С ´ (А В) = (С ´ А) (С ´ В);

(А В) ´ С = (A ´ С) (В ´ С), С ´ (А В) = (С ´ А) (С ´ В);

Эти свойства интуитивно ясны.

Проверим для множеств А = <1, 2>, B = <2, 3>и C = <a> равенство (А В) ´ С = (A ´ С) (В ´ С).

Тогда <1, 2, 3>и = <(1, a); (2, a); (3, a)>.

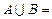
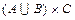
С другой стороны, <(1, a); (2, a)>, <(2, a); (3, a)> и <(1, a); (2, a); (3, a)>.

Как видно, этот пример подтверждает равенство. На этом примере можно проверить и все остальные равенства, приведенные выше.

Однако, пример, подтверждающий равенство, не может служить доказательством этого равенства. Приведем в качестве примера и общее доказательство рассмотренного выше равенства:

и ( или ) и ( и ) или ( и ) или .

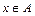
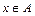
Следовательно, . Обратное включение доказывается точно такой же цепочкой, рассматриваемой лишь с конца.

Можно найти декартово произведение нескольких множеств (двух, трех, …, n множеств).

Источник

Декартово произведение

Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.

Содержание

Прямое произведение в теории множеств

Произведение двух множеств

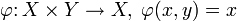
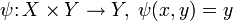
Отображения произведения множеств в его множители ( и ) называют координатными функциями.

Аналогично строятся произведения нескольких множеств.

Декартова степень

Прямое произведение семейства множеств

Прямое произведение отображений

Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.

Воздействие на математические структуры

Прямое произведение групп

Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.

Прямое произведение других алгебраических структур

Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1_i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.

Прямое произведение топологических пространств

Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).

Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).

Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).

Прямое произведение графов

Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:

Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.

Вариации и обобщения

Источник