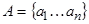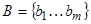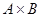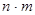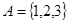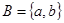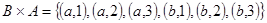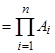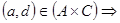Что такое декартово произведение множеств
Декартово произведение
Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.
Содержание
Прямое произведение в теории множеств
Произведение двух множеств
| в | в | в | в | в | в | в | в |
|---|---|---|---|---|---|---|---|
| и | и | и | и | и | и | и | и |
| к | к | к | к | к | к | к | к |
| Произведение множества <в, и, к> на множество цветов радуги | |||||||
Отображения произведения множеств в его множители ( 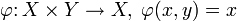
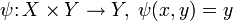
Аналогично строятся произведения нескольких множеств.
Декартова степень
Прямое произведение семейства множеств
Прямое произведение отображений
Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.
Воздействие на математические структуры
Прямое произведение групп
Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.
Прямое произведение других алгебраических структур
Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.
Прямое произведение топологических пространств
Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).
Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).
Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).
Прямое произведение графов
Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:
Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.
Вариации и обобщения
Декартово произведение множеств
Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.
Содержание
Прямое произведение в теории множеств
Произведение двух множеств
| в | в | в | в | в | в | в | в |
|---|---|---|---|---|---|---|---|
| и | и | и | и | и | и | и | и |
| к | к | к | к | к | к | к | к |
| Произведение множества <в, и, к> на множество цветов радуги | |||||||
Отображения произведения множеств в его множители ( 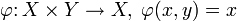
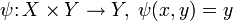
Аналогично строятся произведения нескольких множеств.
Декартова степень
Прямое произведение семейства множеств
Прямое произведение отображений
Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.
Воздействие на математические структуры
Прямое произведение групп
Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.
Прямое произведение других алгебраических структур
Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.
Прямое произведение топологических пространств
Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).
Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).
Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).
Прямое произведение графов
Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:
Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.
Вариации и обобщения
Декартово произведение множеств
Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а; b). Элемент а называют первой координатой (компонентой) пары, а элемент b – второй координатой (компонентой) пары.
Пары (а; b) и (с; d) равны в том и только в том случае, когда а = с и b = d.
В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).
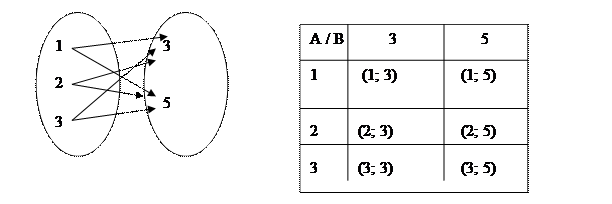
Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, А = <1, 2, 3>, В = <3, 5>. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая компонента – множеству В. Если мы перечислим все такие пары, то получим множества:
Видим, что, имея два множества А.и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.
Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, записывают:
Выясним, какими свойствами обладает операция нахождения декартова произведения. Так как декартовы произведения А х В и В х А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает.
Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности. Но она дистрибутивна относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства:
(А∪В) х С = (А х С) ∪ (В х С),
(А / В) х С = (А х С) / (В х С).
Доказывать эти свойства мы не будем, но проверить их можно на конкретных примерах.
Выясним теперь, как можно наглядно представить декартово произведение множеств.
Если множества А и В конечны и содержат небольшое количество элементов, то его можно изобразить при помощи графа или таблицы. Например, декартово произведение множеств
А = <1, 2, 3>и В = <3, 5>можно представить так, как показано на рисунке.
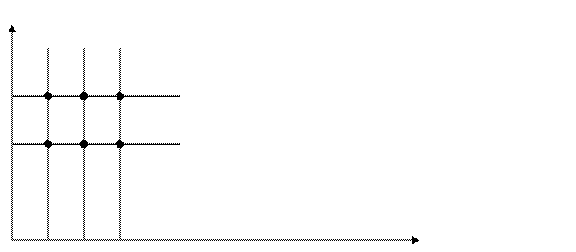
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изобразить на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение выше названных множеств на координатной плоскости будет выглядеть так:
Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В – на оси Оу.
Такой способ наглядного изображения декартова произведения множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.
Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа – это число элементов, из которых он состоит. Например, (3; 6; 7) – это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) – это кортеж длины 10.
Рассматривают в математике и декартово произведение трех, четырех и вообще n множеств.
Декартово произведение множеств А₁, А₂, …, Аn обозначают так:
Декартово произведение множеств. Свойства декартова произведения. Число элементов декартова произведения конечных множеств



Упорядоченной парой (а,в) называется набор элементов а и в, в котором а считается первым, а в – вторым. (а;в) а-первая компонента; в-вторая компонента.
(а;в)=(с;d)óa=c и в=d Декартовым произведением множеств А и В называются множества всех упорядоченных пар, в которых первая компонента принадлежит множеству А, а вторая множеству В.
АхВ≠ВхА, таким образом, декартово произведение коммуникативно, не ассоциативно.
Свойства:1. Не обладает комуникативностью и ассоциативностью.
2. Дистрибутивность относительно объединения и вычитания множеств.
Для любых трёх множеств А,В,С выполняются равенства:
(АUВ)хС=(АхС)U(ВхС) относительно объединения
(А/В)хС=(АхС)\(ВхС) относительно разности
Упорядоченные наборы из более чем двух элементов называются кортежами. Длина кортежа – это число элементов. АхВхСхD=
Число элементов декартова произведения конечных множеств
В классе 40 человек, 34 человека ходят в секцию баскетбола, а 23 – в волейбольную секцию, при этом 18 человек посещают обе эти секции. Сколько человек в классе не посещают ни волейбольную, ни баскетбольную секции?
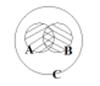
В-мн-во учащихся, посещающих волейбольную секцию.
С-мн-во учащихся класса.
n (A)=34 n (B)=23 n (A∩B)=18 n (C)=40
Число элементов декартова произведения конечных множеств равно произведению числа элементов составляющих множеств. N(AxB)=n(A)?n(B)
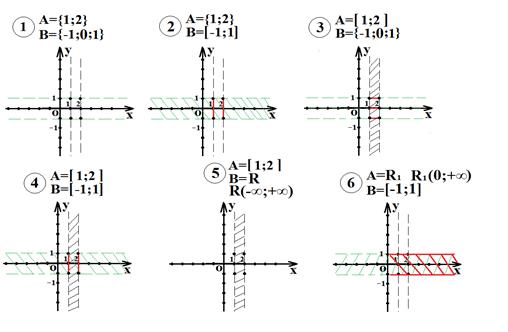
Изображение декартова произведения числовых множеств на координатной плоскости.
Если множества А и В – числовые то их декартово произведение можно изобразить точками на координатной плоскости.
2. Обучающимся начальных классов предложено задание:
“Не вычисляя значения выражений вставить вместо * знаки >,
3) Какое свойство закрепляется при выполнении данного задания? Как оно называется в математике? В данном задании закрепляется переместительное свойство умножения. В математике оно называется коммутативным
4) Опишите методику ознакомления учащихся начальной школы с этим свойством умножения. После изучения таблицы умножения на число 3, детей знакомят с переместительным свойством умножения. В качестве подготовительной работы повторяют формулировку переместительного свойства сложения (от перестановки мест слагаемых сумма не меняется) 25+43=43+25
Повторяют название компонентов и результата действия умножения


2 пример: предлагают разными способами посчитать количество кругов

— Что можно сказать о правых частях примера? (они равны)
— А что можно сказать о левых частях примера? (множители одинаковые, но стоят на разных местах примера 4*3=3*4
5) Какое свойство напоминает эта запись?
Переместительное свойство умножения
Вывод: от перестановки множителей произведение не меняется
Закрепление материала строится на решение примера без иллюстрации
Декартово произведение множеств
Основные операции над множествами
Свойства операций над множествами
Операции над множествами, сформулированные в (1.4) обладают некоторыми свойствами, приведенными в табл. 1. Эти свойства выражаются совокупностью тождеств, справедливых независимо от конкретного содержания входящих в них множеств, являющихся подмножествами некоторого универсума U.
Таблица 1
Основные свойства операций над множествами
1а) 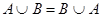 | 1б)  |
2а) 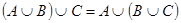 | 2б) 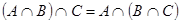 |
3а) 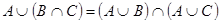 | 3б) 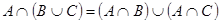 |
4а) 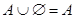 | 4б) 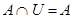 |
5а) 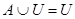 | 5б) 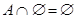 |
6а) 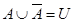 | 6б)  |
7а) 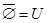 | 7б) 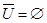 |
8а) 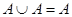 | 8б)  |
9а) 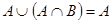 | 9б)  |
10а)  | 10б) 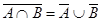 |
11)  | |
12)  | |
13) 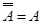 — закон двойного отрицания — закон двойного отрицания | |
14) 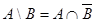 | |
15) 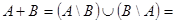 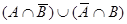 | |
16) 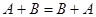 | |
| 17) (А + В) + С = А + (В + С) | |
| 18) А + Æ = Æ + А | |
19) 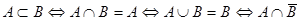 =Æ =Æ | |
20) 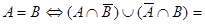 Æ Æ |
Соотношения (11)-(20) отражают свойства дополнения, разности, дизъюнктивной суммы, включения и равенства.
При замене в любой теореме входящих в нее символов дуальными получим новое предложение, которое также является теоремой (принцип двойственности или дуальности). Тождество (11) не изменяется при замене символов дуальными, поэтому его называют самодвойственным.
Декартово произведение множеств
Декартово произведение множеств A и B – это множество упорядоченных пар, первый элемент которых принадлежит A, а второй – принадлежит B.
Пример.
Свойства декартова произведения:
1) 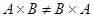
2) 
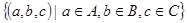
Свойство ассоциативности позволяет использовать сокращенную запись для декартова произведения нескольких множеств:
3) 
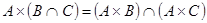
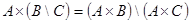
Доказательство: Докажем, например, дистрибутивность декартова произведения относительно операции пересечения множеств.
1) 
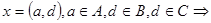

2) 
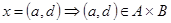
Особым случаем декартова произведения является произведение множества самого на себя. В этом случае говорят о декартовом квадрате множества или декартовой n-ой степени множества А.

Пример. 
Теорема. Если множество A содержит n элементов, а B – m элементов, т.е.: