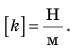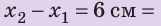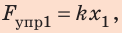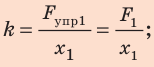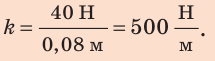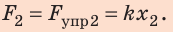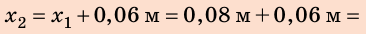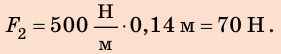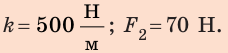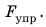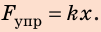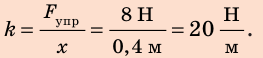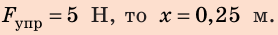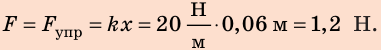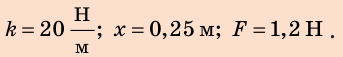Что такое деформация в физике 7 класс
Сила упругости
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
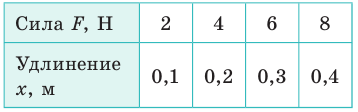
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
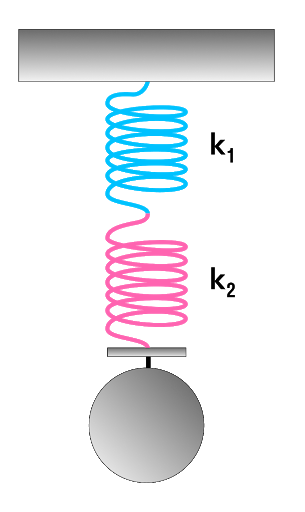
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
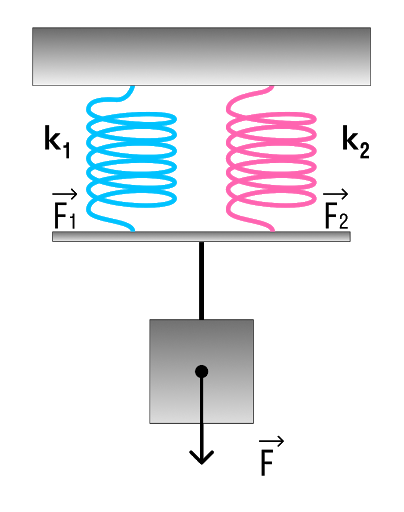
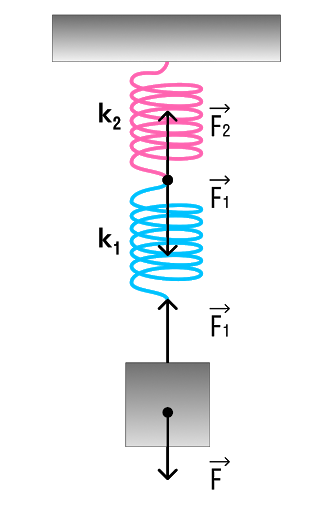
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
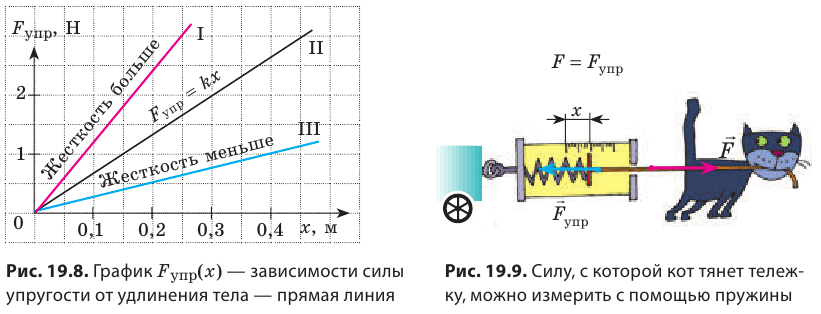
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
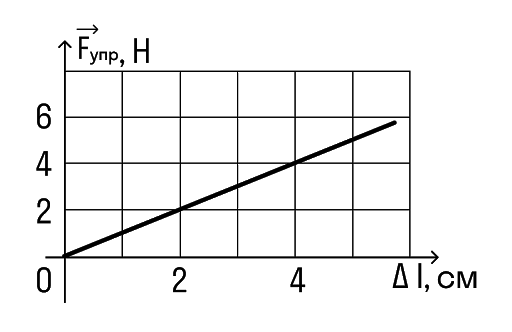
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
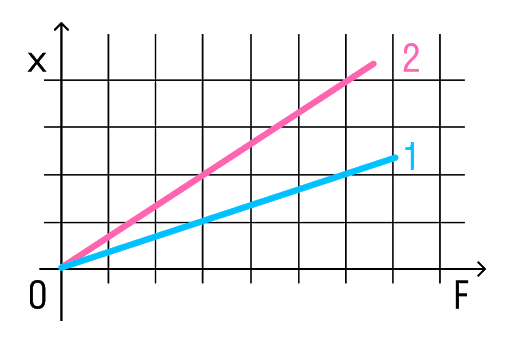
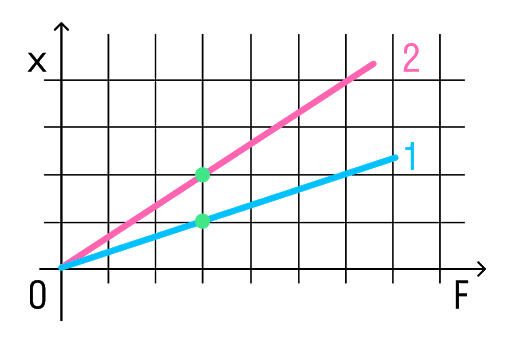
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Содержание:
Деформация тела:
Вспомните ненастный день: дует порывистый ветер, гнутся деревья. Чем сильнее ветер, тем больше гнутся деревья. А вот физики говорят, что деревья деформируются. Когда ветер стихает, деревья возвращаются в свое первоначальное положение — деформация исчезает. Но если ветер достаточно сильный, то ветви деревьев и даже их стволы могут сломаться.
Виды деформации
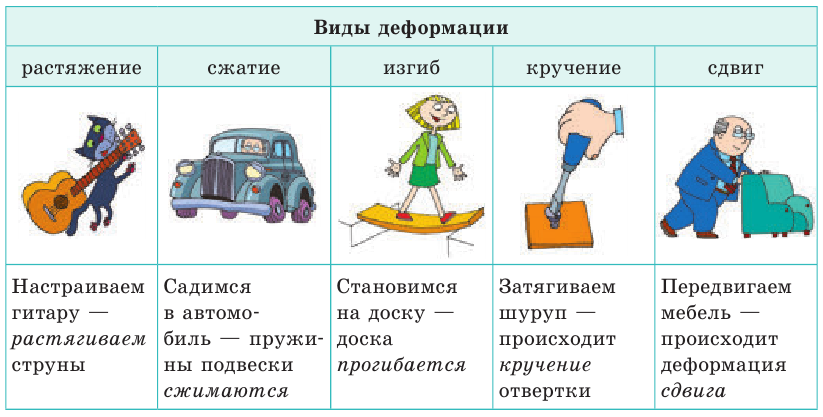
Уже отмечалось, что результатом действия силы на тело может быть как изменение скорости движения тела, так и его деформация. Например, если толкнуть мячик, то он придет в движение, а некоторые его части при толчке сместятся относительно друг друга — мячик деформируется.
Деформация — изменение формы и (или) размеров тела. В зависимости от того, как именно части тела смещаются относительно друг друга, различают деформации растяжения, сжатия, изгиба, кручения, сдвига (см. таблицу).
Различия упругих и пластических деформаций
Возьмите эспандер (или ластик) и сожмите его — эспандер согнется. Но если прекратить сжимать эспандер, он полностью восстановит свою форму — деформация исчезнет (рис. 19.1). Деформации, которые полностью исчезают после прекращения действия на тело внешних сил, называют упругими.
Делая глиняную фигурку, мастер мнет руками комок глины, и глина сохранит форму, которую придаст ей мастер (рис. 19.2). Тяжелый пресс на монетном дворе чеканит монеты из металлических заготовок, — после прекращения действия пресса монета не восстановит свою прежнюю форму куска металла. И глина, и металл «не помнят» своей формы до деформации и не восстанавливают ее. Деформации, которые сохраняются после прекращения действия на тело внешних сил, называют пластическими. Попробуйте привести другие примеры упругих и пластических деформаций.
Определение силы упругости
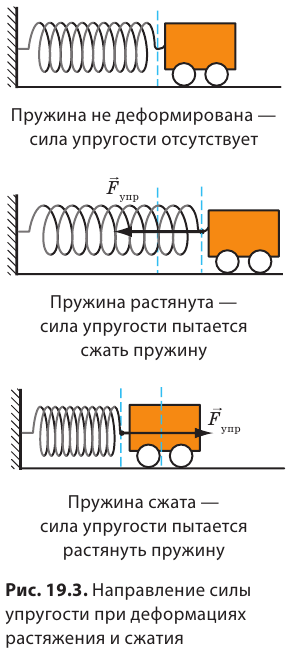
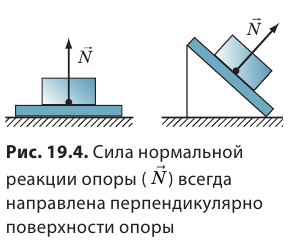
При деформации всегда возникает сила, стремящаяся восстановить то состояние тела, в котором оно находилось до деформации. Эту силу называют силой упругости (рис. 19.3).
Сила упругости — это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации. Обычно силу упругости обозначают символом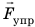 
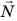
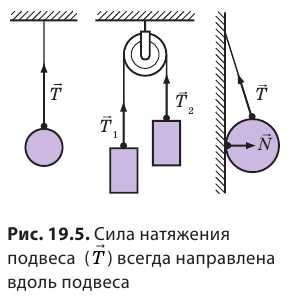
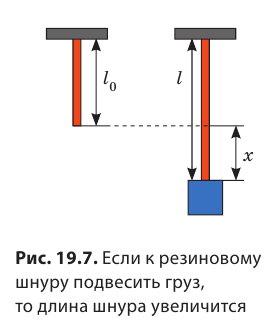
, но в некоторых случаях используют и другие символы. Если тело давит на опору, то опора деформируется (прогибается). Деформация опоры вызывает появление силы упругости, действующей на тело перпендикулярно поверхности опоры. Эту сила называют силой нормальной реакции опоры и обозначаются символом 
(рис. 19.4).
Если тело растягивает подвес (нить, жгут, шнур), то возникает сила упругости, направленная вдоль подвеса. Эту силу называют силой натяжения подвеса и обозначают символом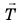 
(рис. 19.5).
Закон Гука
Научное исследование процессов растяжения и сжатия тел начал Роберт Гук (рис. 19.6) в XVII в. Результатом работы ученого стал закон, который позже получил название закон Гука: При малых упругих деформациях растяжения или сжатия сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: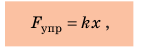 
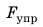
где 
— сила упругости; x — удлинение тела; k — коэффициент пропорциональности, который называют жесткостью тела.
Удлинение — это физическая величина, которая характеризует деформации растяжения и сжатия и равна изменению длины тела в результате деформации. Удлинение х определяется по формуле: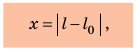 
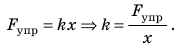
где l — длина деформированного тела; 
— длина недеформированного тела (рис. 19.7). Жесткость тела можно определить, воспользовавшись законом Гука: 
Единица жесткости в СИ — ньютон на метр: 
Жесткость — это характеристика тела, поэтому она не зависит ни от силы упругости, ни от удлинения. Жесткость зависит от формы и размеров тела, а также от материала, из которого тело изготовлено. Сила упругости прямо пропорциональна удлинению тела, поэтому график зависимости 
— прямая (рис. 19.8). Чем больше жесткость тела, тем выше расположен график. Воспользовавшись графиками на рис. 19.8, определите жесткость тел І–ІІІ и убедитесь в справедливости последнего утверждения.
Почему возникает сила упругости
Вы хорошо знаете, что все тела состоят из частиц (атомов, молекул, ионов). В твердых телах частицы колеблются около положений равновесия и взаимодействуют межмолекулярными силами притяжения и отталкивания. В положениях равновесия данные силы уравновешены. При деформации тела во взаимном расположении его частиц происходят изменения. Если расстояние между частицами увеличивается, то межмолекулярные силы притяжения становятся больше сил отталкивания. Если же частицы сближаются, то больше становятся межмолекулярные силы отталкивания. Другими словами: при деформации частицы «стремятся» вернуться в положение равновесия. Силы, возникающие при изменении положения одной частицы, очень малы. Но когда тело деформируется, изменяется взаимное расположение огромного количества частиц. В результате сложение сил дает заметную равнодействующую, которая противостоит деформации тела. Это и есть сила упругости. Итак, сила упругости — проявление действия межмолекулярных сил.
Приборы для измерения силы
Сила — это физическая величина, поэтому ее можно измерить. Приборы для измерения силы называют динамометрами. Основная составляющая простейших динамометров — пружина. Рассмотрим принцип действия таких динамометров на простом примере. Чтобы с помощью пружины, жесткость k которой известна, измерить силу F, с которой кот тянет тележку (рис. 19.9), необходимо:
1) измерить удлинение x пружины; 2) воспользовавшись законом Гука, определить силу упругости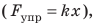 
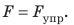
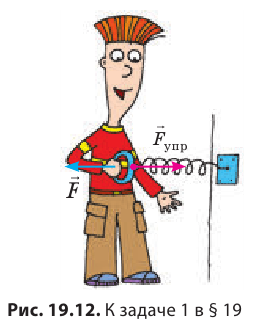
которая действует на кота со стороны пружины и по значению равна силе F тяги кота: 
Понятно, что каждый раз измерять удлинение пружины и рассчитывать силу неудобно. Поэтому пружину закрепляют на панели со шкалой, проградуированной в единицах силы. Именно так устроены простейшие школьные лабораторные динамометры (рис. 19.10). Существуют и другие виды пружинных динамометров (см., например, рис. 19.11).
Пример №1
Действуя на пружину силой 40 Н, мальчик растянул ее на 8 см. Определите жесткость пружины. Какую силу нужно приложить мальчику, чтобы растянуть эту пружину еще на 6 см? Деформацию пружины считайте малой упругой. Анализ физической проблемы. Сила, которую прикладывает мальчик, по значению равна силе упругости, возникающей при растяжении пружины: F= уFпр (рис. 19.12). Деформация является малой упругой, поэтому воспользуемся законом Гука. Задачу будем решать в единицах СИ.
,
,
,
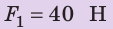
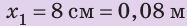
Решение:
1. Вычислим жесткость пружины:
поэтому 
2. Найдем силу, которую нужно приложить мальчику, чтобы дополнительно растянуть пружину:
По условию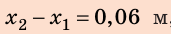 
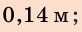
,поэтому 
следовательно,
Анализ результатов. Для удлинения пружины на 8 см мальчик прикладывал силу 40 Н; для удлинения пружины еще на 6 см ему нужно увеличить силу на 30 Н — это правдоподобный результат.
Ответ:
Пример №2
Выполняя экпериментальное задание, девочка увеличивала нагрузку на резиновый шнур. Каждый раз она измеряла силу, действующую на шнур, и соответствующее удлинение шнура. Воспользовавшись таблицей, составленной девочкой, постройте график уFпр(x). С помощью графика определите: 1) жесткость шнура; 2) удлинение шнура, когда к нему приложена сила 5 Н; 3) силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 6 см.
Анализ физической проблемы. При растяжении шнура возникает сила упругости, которая по значению равна силе, действующей на шнур: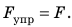 
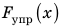
Для построения графика зависимости 
начертим две взаимно перпендикулярных оси. На горизонтальной оси будем откладывать удлинение x шнура, а на вертикальной — соответствующее значение силы упругости 
Решение:
Построив указанные в таблице точки (см. рисунок), увидим, что все они принадлежат одной прямой, значит, для любой точки графика имеем:
1) Выбрав точку А графика, найдем жесткость шнура:
2) Удлинение шнура в результате действия силы 5 Н найдем по графику: если 
3) Силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 0,06 м, найдем по закону Гука:
Ответ:
Итоги:
Деформацией называют изменение формы и (или) размеров тела. Если после прекращения действия на тело внешних сил деформация полностью исчезает, то это упругая деформация; если деформация сохраняется, то это пластическая деформация.
Сила упругости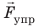 
— это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации.
Сила упругости — проявление действия межмолекулярных сил. При малых упругих деформациях растяжения и сжатия выполняется закон Гука: сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: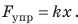 
Приборы для измерения силы называют динамометрами. Простейшие из них — пружинные динамометры.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Что такое деформация в физике 7 класс
Код ОГЭ 1.12. Деформация тела. Упругие и неупругие деформации. Закон упругой деформации (закон Гука).
Деформация – изменение формы или объёма тела под действием внешних сил. Деформация может быть упругая или неупругая.
Упругая деформация – деформация, при которой после прекращения действия силы размеры и форма тела полностью восстанавливаются.
Изменение длины тела Δl = l – l0, где l0 – начальная длина недеформированного тела, l – длина деформированного тела, принято называть величиной деформации.
Величина деформации – это скалярная физическая величина, которая может быть и положительной (тело растягивается), и отрицательной (тело сжимается).
Сила упругости направлена против смещения частей тела при деформации, возникает в деформируемом теле, но приложена к тому объекту, действием которого вызвана деформация.
Закон Гука : Для малых деформаций модуль силы упругости прямо пропорционален величине деформации: Fупр = k |Δl|, где коэффициент пропорциональности k называется жёсткостью.
Единица измерения жёсткости в системе СИ: Н/м. Жёсткость зависит от материала, формы и размеров деформируемого тела.
Внимание! Если тело отсчёта выбранной ИСО расположить у свободного конца деформируемого тела, то при его деформации координата этого конца тела равна величине деформации. Тогда формула закона Гука, записанного для проекции силы упругости, принимает вид: Fупр.x = –kх. Знак «минус» в этом случае указывает на то, что сила упругости направлена в сторону, противоположную смещению частей тела при деформации.
Величины деформаций, для которых справедлив закон Гука, определяются экспериментально для каждого деформируемого тела.
Внимание! Линейная зависимость между модулем силы упругости и удлинением пружины (закон Гука) лежит в основе способа измерения силы с помощью динамометра.
При этом модуль измеряемой силы равен силе упругости пружины, которая, в свою очередь, рассчитывается по величине деформации. Для правильного измерения силы, растягивающей пружину динамометра, необходимо, чтобы во время измерения динамометр находился в покое или двигался прямолинейно и равномерно! Только в этом случае модуль измеряемой силы и модуль силы упругости равны друг другу.
Частные случаи силы упругости:
Внимание! При решении задач часто используется физическая модель «невесомая нерастяжимая нить». Если нить невесома, то она не рассматривается в качестве отдельного тела, для неё не пишется уравнение движения. Условие невесомости приводит также к тому, что силы упругости, возникающие в нити и приложенные к двум связанным телам, равны по модулю (исключение могут составлять задачи, в которых нить перекинута через весомый блок). Нерастяжимость нити приводит к тому, что связанные ею тела движутся с одинаковым по модулю ускорением.
Конспект урока «Деформация тела».