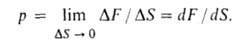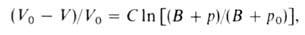Что такое давление химия
Урок 24. Давление газа
В уроке 24 «Давление газа» из курса «Химия для чайников» рассмотрим устройство и принцип действия ртутного барометра, а также дадим определение давлению и рассмотрим его единицы измерения. Не пройдите мимо вводного урока в главу «Законы газового состояния», если вы его еще не читали.
Ртутный барометр
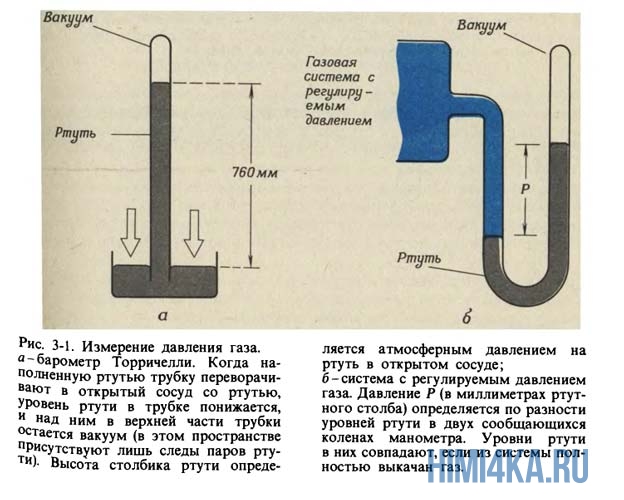
Если стеклянную трубку, закрытую с одного конца, наполнить ртутью (Hg), а затем перевернуть открытым концом в сосуд с ртутью, как показано на рисунке 3-1 (а), уровень ртути в трубке будет опускаться до тех пор, пока высота ртутного столбика над поверхностью ртути в сосуде не достигнет приблизительно 760 миллиметров (мм).
Давление, оказываемое на поверхность ртути в сосуде весом ртутного столбика в трубке, в точности уравновешивается давлением окружающей атмосферы. Вследствие равенства этих давлений, действующих в противоположных направлениях, ртуть больше не выливается из трубки. Подобное устройство называется ртутным барометром. Его изобрел и впервые протестировал итальянский математик и физик Эванджелиста Торричелли для измерения атмосферного давления. Торричелли показал, что высота столбика ртути в барометрической трубке НЕ зависит от формы и размеров трубки, а потому, определяется не весом ртутного столбика, а давлением у его основания. Атмосферное давление на уровне моря поддерживает столбик ртути высотой 760 мм (в среднем). Поскольку в старину для измерения давления пользовались именно ртутными барометрами, то в качестве единицы измерения давления применялся «миллиметр ртутного столба«.
Единицы измерения давления
Представим себе разлитый на столе слой ртути площадью 1 м 2 и толщиной 1 мм. Переведем сначала все размеры этого слоя в сантиметры; тогда его объем выразится как:
Вес этого слоя можно найти как произведение его массы на ускорение силы тяжести, которое равно g = 9,8 м/c 2 ; таким образом, сила, с которой рассматриваемый слой ртути давит на стол, равна:
Пример 2. Стандартное давление на уровне моря считается равным точно 760 мм Hg. Выразите это давление в паскалях.
Из примера 1 мы уже знаем, что давление 1 мм Hg эквивалентно 133,32 Па. Следовательно:
Паскаль — слишком маленькая единица для измерения давлений газов, подобно тому как кубический метр — слишком неудобная единица для измерения объемов жидкостей в лабораторных условиях. Поэтому обычно давление газов измеряют в стандртных атмосферах:
Пример 3. В горах, высота которых составляет около 2500 м над уровнем моря, атмосферное давление приблизительно равно 3/4 давления на уровне моря. Выразите это давление в стандартных атмофсерах, паскалях и миллиметрах ртутного столба.
Ответ: давление равно 0,750 атм, 76 000 Па или 570 мм Hg
Надеюсь урок 24 «Давление газа» помог создать некоторое представление о понятии давления и его единицах измерения. Если у вас возникли вопросы, пишите их в комментарии. Если вопросов нет, то переходите к следующему уроку.
Давление в жидкостях и газах. Закон Паскаля.
теория по физике 🧲 гидростатика
Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.
Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p — давление столба жидкости (Па), ρж— плотность жидкости (кг/м 3 ), g — ускорение свободного падения (≈10 м/с 2 ), h — высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
Подсказки к задачам:
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
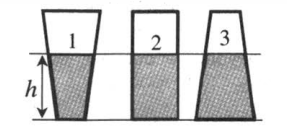
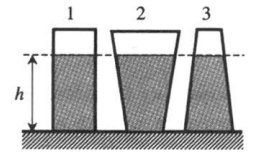
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 3 ), во втором — керосин (ρ2 = 0,8 г/см 3 ), в третьем — спирт (ρ3 = 0,8 г/см 3 ). В каком сосуде оказывается максимальное давление на дно?
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.
Алгоритм решения
Решение
Запишем исходные данные:
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Запишем исходные данные:
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
Алгоритм решения
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
pазбирался: Алиса Никитина | обсудить разбор | оценить
зМБЧБ 1. пУОПЧОЩЕ ЪБЛПОЩ ИЙНЙЙ

1.2 зБЪПЧЩЕ ЪБЛПОЩ ИЙНЙЙ
1.2.1 ъБЛПО бЧПЗБДТП Й УМЕДУФЧЙЕ ЙЪ ОЕЗП
уТЕДЙ ЧЕЭЕУФЧ У ТБЪМЙЮОЩН БЗТЕЗБФОЩН УПУФПСОЙЕН ОЕПВИПДЙНП ЧЩДЕМЙФШ ЗБЪЩ, ЛПФПТЩЕ ЙЗТБАФ ПЗТПНОХА ТПМШ ОЕ ФПМШЛП Ч ОБЫЕК ЦЙЪОЙ, ОП Ч ТБЪМЙЮОЩИ ФЕИОПМПЗЙЮЕУЛЙИ РТПГЕУУБИ. оЕПВИПДЙНП РПНОЙФШ, ЮФП ДМС ЛПМЙЮЕУФЧЕООПК ИБТБЛФЕТЙУФЙЛЙ МАВПЗП ЗБЪБ ЙУРПМШЪХАФ ДБЧМЕОЙЕ, ФЕНРЕТБФХТХ Й ЪБОЙНБЕНЩК ПВЯЕН. оБЙВПМЕЕ ЮБУФП РТЙНЕОСАФ ФБЛ ОБЪЩЧБЕНЩЕ ОПТНБМШОЩЕ ХУМПЧЙС (О.Х.), ЛПФПТЩЕ УППФЧЕФУФЧХАФ ДБЧМЕОЙА т=10 5 рБ Й ФЕНРЕТБФХТЕ ф=273 л.
уПЗМБУОП ЪБЛПОХ бЧПЗБДТП: ПДЙОБЛПЧЩЕ ПВЯЕНЩ ТБЪМЙЮОЩИ ЗБЪПЧ РТЙ ПДЙОБЛПЧЩИ ХУМПЧЙСИ (ДБЧМЕОЙЙ Й ФЕНРЕТБФХТЕ) УПДЕТЦБФ ПДЙОБЛПЧПЕ ЮЙУМП НПМЕЛХМ.
вПМШЫПЕ РТБЛФЙЮЕУЛПЕ ЪОБЮЕОЙЕ ЙНЕЕФ УМЕДУФЧЙЕ ЙЪ ЪБЛПОБ бЧПЗБДТП: РТЙ ОПТНБМШОЩИ ХУМПЧЙСИ (О.Х.) ПДЙО НПМШ МАВПЗП ЗБЪБ ЪБОЙНБЕФ ПВЯЕН, ТБЧОЩК 22,4 М.
пВЯЕН 22,4 М ОБЪЩЧБАФ НПМСТОЩН (НПМШОЩН) ПВЯЕНПН ЗБЪБ Й ПВПЪОБЮБАФ УППФЧЕФУФЧЕООП VM = 22,4 М/НПМШ.
рТЙНЕТ: ХЗМЕЛЙУМЩК ЗБЪ CO2. йНЕЕН н(CO2) = 44 З/НПМШ. ъОБЮЙФ, ПДЙО НПМШ CO2 ЙНЕЕФ НБУУХ 44 З Й ЪБОЙНБЕФ ПВЯЕН (РТЙ О.Х.), ТБЧОЩК 22,4 М, Б ФБЛЦЕ УПДЕТЦЙФ Ч ЬФПН ПВЯЕНЕ 6,02·10 23 НПМЕЛХМ ЗБЪБ.
оЕФТХДОП РПЛБЪБФШ, ЮФП УЧСЪШ НЕЦДХ НБУУПК m Й ПВЯЕНПН V ЛПОЛТЕФОПЗП ЗБЪБ РТЙ О.Х. ПРТЕДЕМСЕФУС ЖПТНХМПК:
 | (1.3) |
еУМЙ ХУМПЧЙС, Ч ЛПФПТЩИ ОБИПДЙФУС ЗБЪ ПФМЙЮБЕФУС ПФ ОПТНБМШОЩИ, ФП ЙУРПМШЪХАФ ХТБЧОЕОЙЕ нЕОДЕМЕЕЧБ-лМБРЕКТПОБ, ЛПФПТПЕ УЧСЪЩЧБЕФ ЧУЕ ПУОПЧОЩЕ РБТБНЕФТЩ ЙДЕБМШОПЗП ЗБЪБ:
 | (1.4) |
1.2.2 ъБЛПО дБМШФПОБ
еУМЙ НЩ ЧЕТОЕНУС Л ХТБЧОЕОЙА ИЙНЙЮЕУЛПК ТЕБЛГЙЙ, ТБУУНБФТЙЧБЕНПК Ч ТБЪДЕМЕ 1.1.1, ФП, У ХЮЕФПН НПМСТОЩИ ПВЯЕНПЧ ЗБЪПЧ, ЕЗП НПЦОП РТЕДУФБЧЙФШ Ч УМЕДХАЭЕН ЧЙДЕ
йЪ РТЙЧЕДЕООПЗП РТЙНЕТБ ЧЙДОП, ЮФП НБУУЩ ЗБЪПЧ ЪБНЕОЕОЩ ОБ НПМШОЩЕ ПВЯЕНЩ. пФУАДБ УМЕДХЕФ ЖПТНХМЙТПЧЛБ ЪБЛПОБ дБМШФПОБ: ПВЯЕНЩ ТЕБЗЙТХАЭЙИ ЗБЪПЧ Й РТПДХЛФПЧ ЙИ ТЕБЛГЙК ПФОПУСФУС ДТХЗ Л ДТХЗХ ЛБЛ ОЕВПМШЫЙЕ ГЕМЩЕ ЮЙУМБ (ЛПЬЖЖЙГЙЕОФЩ ХТБЧОЕОЙС ТЕБЛГЙЙ).
1.2.3 ъБЛПО РБТГЙБМШОЩИ ДБЧМЕОЙК
оБ РТБЛФЙЛЕ ЮБУФП РТЙИПДЙФУС ЧУФТЕЮБФШУС УП УНЕУША ТБЪМЙЮОЩИ ЗБЪПЧ (ОБРТЙНЕТ, ЧПЪДХИ), ч ЬФПН УМХЮБЕ ОЕПВИПДЙНП РТЙНЕОСФШ ЧЩЫЕТБУУНПФТЕООЩЕ ЗБЪПЧЩЕ ЪБЛПОЩ ДМС ЛБЦДПЗП ЗБЪБ Ч ПФДЕМШОПУФЙ Й ЪБФЕН УХННЙТПЧБФШ РПМХЮЕООЩЕ ЧЕМЙЮЙОЩ. рТЙ ЬФПН РПМШЪХАФУС ФБЛЦЕ ЪБЛПОПН РБТГЙБМШОЩИ ДБЧМЕОЙК: ПВЭЕЕ ДБЧМЕОЙЕ ЗБЪПЧПК УНЕУЙ ТБЧОП УХННЕ РБТГЙБМШОЩИ ДБЧМЕОЙК ПФДЕМШОЩИ ЗБЪПЧ, УПУФБЧМСАЭЙИ ДБООХА УНЕУШ, ФП ЕУФШ
пРТЕДЕМЙН У РПНПЭША ХТБЧОЕОЙС нЕОДЕМЕЕЧБ-лМБРЕКТПОБ РБТГЙБМШОЩЕ ДБЧМЕОЙС ЛБЦДПЗП ЙЪ ЗБЪПЧ, УПУФБЧМСАЭЙИ ДБООХА ЗБЪПЧХА УНЕУШ:
т(о2) = (m/M)RT/V = (4З/2З/НПМШ)·8,31·273л/0,0112Н Ъ = 4·105 рБ,
т(уп) = (14З/28З/НПМШ)·8,31·273л/0,0112Н Ъ = 10 5 рБ,
т(N2) = (56З/28З/НПМШ)·8,31·273л/0,0112Н Ъ = 4·10 5 рБ.
пВЭЕЕ ДБЧМЕОЙЕ ЗБЪПЧПК УНЕУЙ ТБЧОП:
чЕМЙЮЙОБ РБТГЙБМШОПЗП ДБЧМЕОЙС ПРТЕДЕМСЕФУС ОЕУЛПМШЛЙНЙ УРПУПВБНЙ, ОП ОБЙВПМЕЕ ЮБУФП ЧУФТЕЮБАЭЙКУС РТБЛФЙЮЕУЛЙ УРПУПВ ПУОПЧБО ОБ ЙУРПМШЪПЧБОЙЙ ЖПТНХМЩ
 | (1.6) |
рТЙНЕТ: ПРТЕДЕМЙФШ НБУУХ ЛЙУМПТПДБ п2, УПДЕТЦБЭЕЗПУС Ч 1 Н Ъ ЧПЪДХИБ РТЙ ОПТНБМШОЩИ ХУМПЧЙСИ, ЕУМЙ РТПГЕОФОПЕ УПДЕТЦБОЙЕ ЛЙУМПТПДБ Ч ЧПЪДХИЕ УПУФБЧМСЕФ 21ПВ.%
рБТГЙБМШОПЕ ДБЧМЕОЙЕ п2 Ч ЧПЪДХИЕ ПРТЕДЕМСЕН РП ЖПТНХМЕ
т(п2) = 10 5 рБ·21%/100% = 0,21·10 5 рБ
пФУАДБ, УПЗМБУОП ХТБЧОЕОЙС нЕОДЕМЕЕЧБ-лМБРЕКТПОБ
m(O2) = PVM/RT = (0,21·10 5 рБ·1Н Ъ ·32З/НПМШ)/8,31·273л = 297 З
тБУУНПФТЙН ЧПЪНПЦОПУФШ ХЮЕФБ ЙЪНЕОЕОЙС ПВЯЕНБ ЙМЙ ДБЧМЕОЙС РТЙ РТПФЕЛБОЙЙ ИЙНЙЮЕУЛПК ТЕБЛГЙЙ, Ч ЛПФПТПК ХЮБУФЧХАФ ЙМЙ ПВТБЪХАФУС ЗБЪППВТБЪОЩЕ РТПДХЛФЩ. дМС ХЮЕФБ ЬФПЗП ОЕПВИПДЙНП ЧУРПНОЙФШ, ЮФП ЛПЬЖЖЙГЙЕОФЩ Ч ХТБЧОЕОЙЙ ИЙНЙЮЕУЛПК ТЕБЛГЙЙ РТСНП РТПРПТГЙПОБМШОЩ ЮЙУМХ НПМЕК ТЕБЗЙТХАЭЙИ Й ПВТБЪХАЭЙИУС ЧЕЭЕУФЧ. рТЙНЕОЙФЕМШОП Л ЗБЪБН ОЕПВИПДЙНП ХЮЕУФШ ФБЛЦЕ, ЮФП:
фБЛЙН ПВТБЪПН, УТБЧОЙЧБС ЛПЬЖЖЙГЙЕОФЩ ЙУИПДОЩИ ЧЕЭЕУФЧ Й РТПДХЛФПЧ ТЕБЛГЙЙ, НПЦОП УДЕМБФШ ЧЩЧПД ПВ ЙЪНЕОЕОЙЙ ПВЯЕНБ (ДБЧМЕОЙС) Ч ИПДЕ ИЙНЙЮЕУЛПК ТЕБЛГЙЙ.
оБРТЙНЕТ, Ч ИЙНЙЮЕУЛПК ТЕБЛГЙЙ
ЧУЕ ЧЕЭЕУФЧБ СЧМСАФУС ЗБЪБНЙ, чЙДОП, ЮФП ДП ТЕБЛГЙЙ ЙНЕМПУШ 3 НПМС ЗБЪБ (2 НПМС уп Й 1 НПМШ п2), Б РПУМЕ ТЕБЛГЙЙ ПУФБМПУШ 2 НПМС уп2. сУОП, ЮФП ПВЯЕН 3 НПМЕК ЗБЪБ (22,4·3=67,2М) ВПМШЫЕ ПВЯЕНБ 2 НПМЕК (22,4·2=44,8М), ФП ЕУФШ VОБЮ> VЛПО. ъОБЮЙФ, ДБООБС ТЕБЛГЙС РТПФЕЛБЕФ МЙВП У ХНЕОШЫЕОЙЕН ПВЯЕНБ (ЙЪПВБТОЩК РТПГЕУУ), МЙВП У ХНЕОШЫЕОЙЕ ДБЧМЕОЙС (ЙЪПИПТОЩК РТПГЕУУ).
ч УМХЮБЕ ИЙНЙЮЕУЛПК ТЕБЛГЙЙ
ЙНЕЕН ЗБЪППВТБЪОЩЕ ЧЕЭЕУФЧБ уп2 Й уп Й ФЧЕТДПЕ ЧЕЭЕУФЧП у. уТБЧОЙЧБЕН ЛПЬЖЖЙГЙЕОФЩ ФПМШЛП ДМС ЗБЪППВТБЪОЩИ ЧЕЭЕУФЧ Й ЙНЕЕН ДМС ЙУИПДОЩИ ЧЕЭЕУФЧ 1 Й ЛПОЕЮОЩИ ЧЕЭЕУФЧ 2. фБЛ ЛБЛ 1 

ДАВЛЕНИЕ
физ. величина, характеризующая интенсивность нормальных (перпендикулярных к пов-сти) сил, с к-рыми одно тело действует на пов-сть другого. Д.-один из основных параметров состояния термодинамич. системы, входящий в уравнения состояния (вместе с т-рой и уд. объемом). При равномерном распределении сил вдоль пов-сти Д. ропределяется как сила F, действующая по нормали к пов-сти на площадь S: р = F/S. Если распределение сил по пов-сти неравномерно, рассматривают Д. в данной точке:
При сжатии газов и жидкостей прилагаемая нагрузка распределяется в в-ве изотропно, т. е. Д. по всем направлениям одинаково (гидростатич. Д.). При сжатии твердых тел возникающие в объеме тела напряжения обычно распределяются неравномерно. В этом случае под Д. в данной точке понимают среднее арифметическое нормальных напряжений, действующих в трех взаимно перпендикулярных направлениях.
3000 К), а также при дополнительном наложении напряжений сдвига, вызывающих пластическую деформацию.Динамич. Д., при к-рых выполняются физ.-хим. исследования конденсированных систем, достигают 500 ГПа.
Д. до 1 ГПа обычно измеряют манометрами, свыше 1 ГПа-датчиками из сплавов металлов (напр., манганина), электрическое сопротивление которых зависит от Д.
Сведения о влиянии высоких Д. на физ.-хим. св-ва в-в появились в 19 в. Систематич. изучение поведения в-в при высоких Д. было начато в 20-х гг. 20 в. Основополагающие результаты в этой области были получены П. Бриджменом. В СССР аналогичные исследования были начаты в 30-е гг. Важную роль в развитии исследований физ. и хим. процессов сыграли работы Л. Ф. Верещагина с сотр. В данной статье рассматривается действие на в-во статич. Д.; о физ.-хим. исследованиях при динамич. Д. см. в ст. Взрыв, Ударных труб метод.
Влияние Д. на физ. св-ва в-в. Непосредственным результатом действия Д. является сжатие в-ва, т. е. изменение его объема вследствие изменения межатомных (межмолекулярных) расстояний. Способность в-ва изменять свой объем под действием Д. характеризуется сжимаемостью. С увеличением Д. плотность газов растет и при Д. порядка сотен МПа приближается к плотности жидкостей. При 1 ГПа плотность большинства жидкостей возрастает на 20-30% по сравнению с плотностью при нормальном Д. Для многих металлов при 10 ГПа плотность возрастает на 6-15%, для др. твердых тел-на 15-25%. Изменение объема жидкости или сильно сжатого газа в интервале Д. от нек-рого начального р 0 до значения рм. б. описано ур-нием Тейта:
где 0 и V-объем в-ва при Д. р 0 и р соотв., С и В-эмпирич. постоянные.
Вязкость жидкостей увеличивается с Д. (см. рис. 1). Ди-электрич. проницаемость в-ва обычно возрастает с Д., что обусловлено в основном изменением плотности. Для многих в-в зависимость от Д. удовлетворительно описывается ур-нием:
Под Д. твердые тела нередко претерпевают полиморфные переходы. Так, при 20
ДАВЛЕНИЕ
физ. величина, характеризующая интенсивность нормальных (перпендикулярных к пов-сти) сил, с к-рыми одно тело действует на пов-сть другого. Д.-один из основных параметров состояния термодинамич. системы, входящий в уравнения состояния (вместе с т-рой и уд. объемом). При равномерном распределении сил вдоль пов-сти Д. ропределяется как сила F, действующая по нормали к пов-сти на площадь S: р = F/S. Если распределение сил по пов-сти неравномерно, рассматривают Д. в данной точке:
При сжатии газов и жидкостей прилагаемая нагрузка распределяется в в-ве изотропно, т. е. Д. по всем направлениям одинаково (гидростатич. Д.). При сжатии твердых тел возникающие в объеме тела напряжения обычно распределяются неравномерно. В этом случае под Д. в данной точке понимают среднее арифметическое нормальных напряжений, действующих в трех взаимно перпендикулярных направлениях.
3000 К), а также при дополнительном наложении напряжений сдвига, вызывающих пластическую деформацию. Динамич. Д., при к-рых выполняются физ.-хим. исследования конденсированных систем, достигают 500 ГПа.
Д. до 1 ГПа обычно измеряют манометрами, свыше 1 ГПа-датчиками из сплавов металлов (напр., манганина), электрическое сопротивление которых зависит от Д.
Сведения о влиянии высоких Д. на физ.-хим. св-ва в-в появились в 19 в. Систематич. изучение поведения в-в при высоких Д. было начато в 20-х гг. 20 в. Основополагающие результаты в этой области были получены П. Бриджменом. В СССР аналогичные исследования были начаты в 30-е гг. Важную роль в развитии исследований физ. и хим. процессов сыграли работы Л. Ф. Верещагина с сотр. В данной статье рассматривается действие на в-во статич. Д.; о физ.-хим. исследованиях при динамич. Д. см. в ст. Взрыв, Ударных труб метод.
Влияние Д. на физ. св-ва в-в. Непосредственным результатом действия Д. является сжатие в-ва, т. е. изменение его объема вследствие изменения межатомных (межмолекулярных) расстояний. Способность в-ва изменять свой объем под действием Д. характеризуется сжимаемостью. С увеличением Д. плотность газов растет и при Д. порядка сотен МПа приближается к плотности жидкостей. При 1 ГПа плотность большинства жидкостей возрастает на 20-30% по сравнению с плотностью при нормальном Д. Для многих металлов при 10 ГПа плотность возрастает на 6-15%, для др. твердых тел-на 15-25%. Изменение объема жидкости или сильно сжатого газа в интервале Д. от нек-рого начального р 0 до значения рм. б. описано ур-нием Тейта: