Что такое дамми переменная в статистике

Фиктивная переменная

Фиктивная переменая (англ. dummy variable ) — качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков принимающих два, но и несколько возможных значения. В этом случае добавляются несколько фиктивных переменных. Фиктивная переменная может быть также индикатором принадлежности наблюдения к некоторой подвыборке. Последнее можно использовать для обнаружения структурных изменений.

Содержание

Моделирование бинарной переменной

Пусть необходимо определить влияние некоторой качественной переменной z, принимающей два возможных значения. Обозначим эти возможные значения A и B для определенности. Тогда такой переменной можно поставить в соответствие следующую фиктивную переменную

Пусть исходная модель имеет вид

Если добавить переменную d в модель, то получим

Тогда при значимом коэффициенте при d получаем две модели для разных значений качественного признака, различающиеся на фиксированный сдвиг (разная константа):

Однако, качественный признак может влиять и на параметры зависимости от факторов x. В этом случае необходимо строить модель:

Таким образом, здесь в модели участвует не только переменная d, но и переменная dx. Это позволяет строить потенциально две разные модели для разных значений качественного признака:

Моделирование многозначного качественного признака

Пусть имеется признак, который принимает несколько возможных значений. Общее правило введения фиктивных переменных следующее: общее количество фиктивных переменных должно быть на единицу меньше количества возможных значений качественного признака, если в модели имеется константа. Это необходимо, чтобы не возникла проблема полной коллинеарности переменных.

Например, уровень образования: нет образования, среднее образование, высшее образование, ученая степень и т. д. В этом случае каждому уровню образования, кроме уровня «нет образования» можно поставить в соответствие некоторую фиктивную переменную.

Фиктивные переменные взаимодействия

Пусть в модели (например, средней заработной платы) участвуют две фиктивные переменные, отвечающие, например, за пол и наличие высшего образования. При обычном включении этих переменных в модель каждая из них дает определенный вклад в изменение коэффициентов модели. Однако, сумма эффектов пола и образования вообще говоря может быть не равна суммарному эффекту этих двух факторов, действующих одновременно. То есть наличие высшего образования у мужчин и у женщин вообще говоря по разному может отражаться на доходе. Поэтому наряду с фиктивными переменными пола и образования можно использовать фиктивную переменную взаимодействия:

Таким образом, данная переменная равна 1, например, для мужчин с высшим образованием и равна нулю для всех остальных случаев (мужчин без высшего образования и женщин независимо от уровня образования).

Источник

4.2. Фиктивные переменные

Иногда в процессе эконометрического моделирования у исследователя возникает потребность учитывать в качестве объясняющих факторов не только количественные, но и качественные характеристики. Например, на цену квартиры могут влиять не только её жилая площадь и расстояние до ближайшего метро (количественные переменные), но и материал, из которого изготовлен дом, или наличие в этой квартире балкона (качественные переменные). На величину заработной платы работника могут влиять не только его стаж работы (количественный признак), но и факт наличия у него высшего образования или пол (качественные признаки). Во всех этих случаях удобно использовать так называемые фиктивные переменные.

Фиктивные переменные — это такие переменные, которые принимают одно из двух значений — 0 или 1. Их также называют бинарными или дамми-переменными (dummy variable).

Представим, например, что заработная плата описывается следующим уравнением, для которого выполнены все предпосылки классической линейной модели множественной регрессии:

где \(Y_\) — зарплата i-го работника в долларах в час, \(X_\) — стаж работы i-го работника в годах, \(D_\) — фиктивная переменная, которая равна единице, если i-ый работник — женщина, и равна нулю, если мужчина. Исследователь включает в модель эту переменную потому, что подозревает наличие на рассматриваемом рынке труда дискриминации по гендерному признаку.

В результате МНК-оценивания параметров модели на основе данных о 1000 работниках исследователь получил следующее уравнение:

Результаты построения модели с фиктивной переменной удобно интерпретировать, если записать её для двух случаев: когда фиктивная переменная равна 0 и когда она равна 1. В нашем примере это приведёт к двум вот таким уравнениям:

Отсюда видно, что при прочих равных условиях (при равном стаже работы) женщины получают на 3,5 доллара меньше, чем мужчины. Подчеркнем, что оценка такой модели гораздо лучше, чем просто сравнение средней по выборке заработной платы мужчин со средней по выборке заработной платой женщин, так как гипотетически различие между этими средними могло бы объясняться не гендерной дискриминацией, а разным стажем работы у мужчин и женщин. Мы же в нашем примере контролируем это различие, включая стаж работы в модель. В реальном исследовании, разумеется, было бы целесообразно включить в модель и прочие факторы, которые могут влиять на заработную плату (скажем, образование), однако нам для целей объяснения идеи фиктивных переменных пока хватит этого упрощенного примера.

Графически полученные уравнения представлены на рисунке 4.1. Мы видим, что наша фиктивная переменная отражает сдвиг линии, характеризующей зависимость заработной платы от стажа работы. Поэтому фиктивные переменные такого сорта иногда называют фиктивными переменными сдвига.

Рисунок 4.1. Зависимость между стажем работы и заработной платой для мужчин и для женщин в случае использования фиктивной переменной сдвига.

Включив такое произведение в модель, исследователь получит следующее уравнение:

И снова, чтобы понять, как его интерпретировать, удобно переписать уравнение отдельно для женщин и мужчин:

Рисуснок 4.2. Зависимость между стажем работы и заработной платой для мужчин и для женщин в случае использования фиктивных переменных сдвига и наклона ( \( <\beta_<3>).

Фиктивные переменные могут помочь выявить структурные различия в моделях для разных подвыборок. В нашем примере мы можем проверить наличие или отсутствие структурных различий в моделях заработных плат для мужчин и женщин. Для этого достаточно проверить гипотезу

Действительно, легко видеть, что если эта гипотеза верна, то уравнения заработной платы для мужчин и для женщин являются одинаковыми. Чтобы тестировать эту гипотезу, следует осуществить уже знакомый нам тест для сравнения «короткой» и «длинной» регрессий. Применительно к фиктивным переменным этот тест иногда называют тестом Чоу или тестом на структурный сдвиг. Он устроен следующим образом: необходимо добавить в модель фиктивную переменную сдвига и все соответствующие фиктивные переменные наклона, а затем тестировать гипотезу о том, что коэффициенты при этой фиктивной переменной сдвига и всех фиктивных переменных наклона одновременно равны нулю.

Пример 4.2. Тест на структурный сдвиг.

Опираясь на одну и ту же выборку из 1000 работников, исследователь оценил параметры двух моделей:

В первой модели R-квадрат оказался равен 0,6, а во второй — 0,8. Осуществите тест на структурный сдвиг и интерпретируйте его результаты.

Решение:

Нужно тестировать гипотезу \(\beta_ <3>= \beta_ <4>= 0\) против альтернативной гипотезы о том, что хотя бы один из двух указанных коэффициентов отличен от нуля.

Расчетное значение тестовой статистики может быть определено по формуле:

В рассмотренном нами примере качественный признак может принимать два возможных значения: работник является либо мужчиной, либо женщиной. При помощи фиктивных переменных можно анализировать и случаи большего количества возможных значений.

Представим, что мы в качестве моделируемого признака рассматриваем университет, который закончил работник, и что в выборке есть выпускники ровно трёх университетов: A, B и C (и нет работников, которые не закончили никакого университета). Ясно, что одной бинарной переменной нам уже не хватит, и этот качественный признак нужно закодировать каким-то другим образом. Оказывается, это просто сделать, добавив в модель не одну, а две фиктивные переменные. Тогда уравнение будет выглядеть вот так:

где \(A_\) — фиктивная переменная, которая равна 1, если i-ый респондент является выпускником вуза А, и равна 0 в противном случае, \(B_\) — аналогичная переменная для вуза B.

Дело в том, что если мы добавим 3-ю фиктивную переменную, то мы столкнемся с чистой мультиколлинеарностью. Если i-ый работник закончил университет B, тогда для него \( = 0>, = 1>, = 0>\) и, следовательно

Представим, что мы в нашем примере ограничились двумя фиктивными переменными, собрали данные о трех тысячах выпускников и, проведя необходимые расчеты, получили следующие оценки параметров:

Как интерпретировать полученные оценки коэффициентов? Снова запишем модель для каждого типа выпускников отдельно:

Коэффициент при фиктивной переменной А, оценка которого равна 2, означает, что при прочих равных условиях выпускник вуза А зарабатывает на 2 доллара в час больше, чем выпускник вуза С. Важно помнить, что, когда мы интерпретируем коэффициент, мы должны не просто говорить, что кто-то зарабатывает больше, а указывать, по сравнению с кем больше. В данном случае фраза «выпускник вуза А в среднем получает на 2 доллара в час больше, чем выпускник вуза С» — это корректная фраза. А фраза «выпускник вуза А получает на 2 доллара больше, чем выпускники других вузов» — это некорректная фраза, так как в модели видно, что выпускник вуза А по сравнению с выпускниками вуза В получает не больше, а меньше.

Обычно в качестве базы для сравнения (или так называемой эталонной категории) выступает та категория, для которой мы не стали добавлять фиктивную переменную. В нашем примере эталонным университетом выступает вуз С (эталонным не в том смысле, что он самый хороший, а в том смысле, что с ним все сравнивается).

Или добавить все m фиктивных переменных, но тогда не добавлять константу. Этот вариант менее удобен для содержательной интерпретации результатов, поэтому используется сравнительно редко.↩︎

Источник

Фиктивные переменные часто используются при анализе временных рядов с переключением режимов, сезонным анализом и приложениями для получения качественных данных.

СОДЕРЖАНИЕ

Включение манекена независимого

Модели ANOVA

Модель ANOVA с одной качественной переменной

В этой модели у нас есть только качественные регрессоры, принимающие значение 1, если наблюдение относится к определенной категории, и 0, если оно принадлежит к любой другой категории. Это делает его моделью ANOVA.

Теперь, принимая ожидания обеих сторон, получаем следующее:

Средняя заработная плата учителей государственных школ в Северном регионе:

Средняя заработная плата учителей государственных школ Южного региона:

Средняя заработная плата учителей государственных школ в Западном регионе:

Используя указанные данные, результатом регрессии будет:

se = (1128,523) (1435,953) (1499,615)

т = (23,1759) (-1,2078) (-2,1776)

р = (0,0000) (0,2330) (0,0349)

Модель ANOVA с двумя качественными переменными

Предположим, мы рассматриваем модель ANOVA, имеющую две качественные переменные, каждая из которых имеет две категории: почасовая оплата должна быть объяснена в терминах качественных переменных Семейное положение (женат / не женат) и географический регион (север / не-север). Здесь семейное положение и географический регион являются двумя независимыми фиктивными переменными.

Скажем, результат регрессии на основе некоторых заданных данных выглядит следующим образом:

В этой модели каждой качественной переменной присваивается одна фиктивная переменная, на единицу меньше, чем количество категорий, включенных в каждую.

Таким образом, если в регрессию включено более одной качественной переменной, важно отметить, что пропущенная категория должна быть выбрана в качестве эталонной категории, и все сравнения будут проводиться по отношению к этой категории. Член пересечения покажет ожидание эталонной категории, а коэффициенты наклона покажут, насколько другие категории отличаются от эталонной (опущенной) категории.

Модели ANCOVA

Модель регрессии, которая содержит смесь количественных и качественных переменных, называется моделью анализа ковариации (ANCOVA). Модели ANCOVA являются расширением моделей ANOVA. Они статистически контролируют влияние количественных независимых переменных (также называемых ковариатами или контрольными переменными).

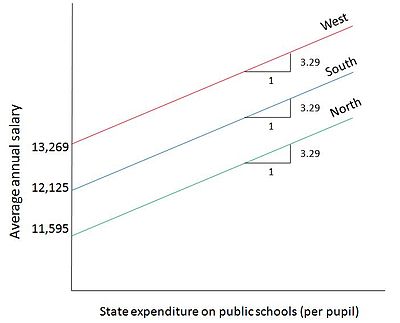
Y _i = средняя годовая зарплата учителей государственных школ в штате i X _i = Государственные расходы на государственные школы на ученика D _2i = 1, если государство i находится в Северном регионе D _2i = 0, иначе D _3i = 1, если государство i находится в Южном регионе D _3i = 0, иначе

Скажем, выход регрессии для этой модели

Результат показывает, что на каждое увеличение государственных расходов на одного ученика в государственных школах на 1 доллар средняя зарплата учителя государственной школы увеличивается примерно на 3,29 доллара. Кроме того, для штата в Северном регионе средняя заработная плата учителей ниже, чем в Западном регионе, примерно на 1673 доллара, а для штата в Южном регионе средняя заработная плата учителей ниже, чем в Западном регионе, примерно на 1144 долларов. На рисунке 3 схематически изображена эта модель. Строки средней заработной платы параллельны друг другу, исходя из предположения модели, что коэффициент расходов не зависит от штата. Компромисс, показанный отдельно на графике для каждой категории, находится между двумя количественными переменными: заработная плата учителей государственных школ (Y) по отношению к государственным расходам на одного ученика в государственных школах (X).

Взаимодействия между фиктивными переменными

Количественные регрессоры в регрессионных моделях часто взаимодействуют друг с другом. Таким же образом качественные регрессоры или фиктивные переменные также могут иметь эффекты взаимодействия друг с другом, и эти взаимодействия могут быть изображены в регрессионной модели. Например, в регрессии, включающей определение заработной платы, если рассматривать две качественные переменные, а именно пол и семейное положение, может существовать взаимосвязь между семейным положением и полом. Эти взаимодействия можно показать в уравнении регрессии, как показано в приведенном ниже примере.

С двумя качественными переменными, являющимися полом и семейным положением, и с количественным объяснением, являющимся количеством лет образования, регрессия, которая является чисто линейной в объяснителях, будет

β ₂ = дифференциальный эффект женского пола β ₃ = дифференциальный эффект от брака β ₄ = дополнительно дифференциальный эффекта быть как женскими и в браке

Таким образом, макет взаимодействия (продукт двух макетов) может изменять зависимую переменную от значения, которое она получает, когда эти два макета рассматриваются по отдельности.

D ₄ = 1, если женщина незамужняя, 0 в противном случае D ₅ = 1, если женатый мужчина, 0 в противном случае D ₆ = 1, если замужняя женщина, 0 в противном случае

тогда достаточно указать регрессию

Фиктивные зависимые переменные

Решение: выбор профессии. Зависимый манекен: супервизор = 1, если супервизор, 0, если не супервизор.

Решение: принадлежность к политической партии. Зависимый пустышка: Принадлежность = 1, если связана с партией, 0, если не аффилирована.

Решение: выход на пенсию. Зависимый манекен: на пенсии = 1, если на пенсии, 0, если не на пенсии.

Когда качественная зависимая фиктивная переменная имеет более двух значений (например, принадлежность ко многим политическим партиям), она становится мультиответной, полиномиальной или полихотомической моделью.

Модели зависимых фиктивных переменных

Линейная вероятностная модель

Модель LPM имеет ряд проблем:

Альтернативы LPM

С этой целью для оценки регрессии зависимой фиктивной переменной можно использовать кумулятивную функцию распределения (CDF). На рисунке 4 показана S-образная кривая, напоминающая CDF случайной величины. В этой модели вероятность находится между 0 и 1, и нелинейность была зафиксирована. Теперь вопрос в выборе используемого CDF.

Логит модель

Недостатки LPM привели к разработке более совершенной и улучшенной модели, названной моделью logit. В модели логита совокупное распределение члена ошибки в уравнении регрессии является логистическим. Регрессия более реалистична в том смысле, что она нелинейна.

Пробит модель

Источник

В статистика и эконометрика, особенно в регрессивный анализ, а фиктивная переменная [а] это тот, который принимает только значение 0 или 1, чтобы указать на отсутствие или наличие некоторого категориального эффекта, который, как можно ожидать, изменит результат. [2] [3] Их можно рассматривать как числовые замены для качественный факты в регрессионная модель, сортировка данных в взаимоисключающий категории (например, курящий и некурящий). [4]

Манекен независимая переменная (также называемая фиктивной объясняющей переменной), которая для некоторых наблюдений имеет значение 0, приведет к тому, что эта переменная коэффициент не иметь роли во влиянии на зависимая переменная, в то время как когда манекен принимает значение 1, его коэффициент действует, чтобы изменить перехватить. Например, предположим, что членство в группе является одной из качественных переменных, относящихся к регрессии. Если членству в группе произвольно присвоено значение 1, тогда все остальные получат значение 0. Тогда перехват будет постоянным членом для нечленов, но будет постоянным членом плюс коэффициент фиктивной принадлежности членства в случае группы члены. [5]

Фиктивные переменные часто используются в анализ временных рядов с переключением режимов, сезонным анализом и приложениями качественных данных.

Содержание

Включение манекена независимого

Модели ANOVA

Модель регрессии, в которой зависимая переменная является количественной по своей природе, но все объясняющие переменные являются фиктивными (качественными по своей природе), называется моделью. Анализ отклонений (ANOVA) модель. [4]

Модель ANOVA с одной качественной переменной

Предположим, мы хотим провести регрессию, чтобы выяснить, различается ли средняя годовая зарплата учителей государственных школ в трех географических регионах в стране A с 51 штатом: (1) Север (21 штат) (2) Юг (17 штатов) (3) Запад (13 штатов). Предположим, что простая арифметическая средняя заработная плата выглядит следующим образом: 24 424,14 доллара (север), 22 894 доллара (юг), 26 158,62 доллара (запад). Среднеарифметические значения разные, но отличаются ли они друг от друга статистически? Чтобы сравнить средние значения, Анализ отклонений регрессионная модель может быть определена как:

В этой модели у нас есть только качественные регрессоры, принимающие значение 1, если наблюдение относится к определенной категории, и 0, если оно принадлежит к любой другой категории. Это делает его моделью ANOVA.

Теперь, принимая ожидание обеих сторон, получаем следующее:

Средняя заработная плата учителей государственных школ в Северном регионе:

Средняя заработная плата учителей государственных школ Южного региона:

Средняя заработная плата учителей государственных школ в Западном регионе:

(Термин ошибки не включается в ожидаемые значения, поскольку предполагается, что он удовлетворяет обычным OLS условий, т.е.E (u_я) = 0)

Ожидаемые значения можно интерпретировать следующим образом: Средняя зарплата учителей государственных школ на Западе равна перехватываемому члену α₁ в уравнении множественной регрессии и дифференциальных коэффициентах пересечения, α₂ и α₃, объясните, насколько средняя заработная плата учителей в Северном и Южном регионах отличается от заработной платы учителей на Западе. Таким образом, средняя заработная плата учителей на Севере и Юге составляет в сравнении против средней зарплаты учителей на Западе. Следовательно, Западный регион становится базовая группа или эталонная группа, то есть группа, с которой производятся сравнения. В пропущенная категорият. е. категория, которой не назначен манекен, принимается в качестве категории основной группы.

Используя указанные данные, результатом регрессии будет:

se = (1128,523) (1435,953) (1499,615)

т = (23,1759) (-1,2078) (-2,1776)

р = (0,0000) (0,2330) (0,0349)

Чтобы выяснить, отличаются ли средние зарплаты учителей на Севере и Юге статистически от зарплат учителей на Западе (категория сравнения), мы должны выяснить, равны ли коэффициенты наклона результата регрессии статистически значимый. Для этого необходимо учитывать п значения. Расчетный коэффициент наклона для Севера статистически не значим, так как его п значение составляет 23 процента; тем не менее, показатель Юга статистически значим на уровне 5%, поскольку его п значение составляет всего около 3,5%. Таким образом, общий результат состоит в том, что средние зарплаты учителей на Западе и Севере статистически не отличаются друг от друга, но средняя заработная плата учителей на Юге статистически ниже, чем на Западе, примерно на 3265 долларов. Модель схематически показана на рисунке 2. Эта модель представляет собой модель ANOVA с одной качественной переменной, имеющей 3 категории. [4]

Модель ANOVA с двумя качественными переменными

Предположим, мы рассматриваем модель ANOVA, имеющую две качественные переменные, каждая из которых имеет две категории: почасовая заработная плата должна быть объяснена с точки зрения качественных переменных Семейное положение (женат / не женат) и географический регион (север / не-север). Здесь семейное положение и географический регион являются двумя независимыми фиктивными переменными. [4]

Скажем, результат регрессии на основе некоторых заданных данных выглядит следующим образом:

В этой модели каждой качественной переменной присваивается одна фиктивная переменная, на единицу меньше, чем количество категорий, включенных в каждую.

Таким образом, если в регрессию включено несколько качественных переменных, важно отметить, что пропущенная категория должна быть выбрана в качестве эталонной категории, и все сравнения будут производиться по отношению к этой категории. Член пересечения покажет ожидаемое значение эталонной категории, а коэффициенты наклона покажут, насколько другие категории отличаются от эталонной (пропущенной) категории. [4]

Модели ANCOVA

Модель регрессии, которая содержит смесь количественных и качественных переменных, называется Анализ ковариации (ANCOVA) модель. Модели ANCOVA являются расширением моделей ANOVA. Они статистически контролируют влияние количественных независимых переменных (также называемых ковариатами или контрольными переменными). [4]

Чтобы проиллюстрировать, как качественные и количественные регрессоры включаются в модели ANCOVA, предположим, что мы рассматриваем тот же пример, который используется в модели ANOVA с одной качественной переменной: среднегодовая зарплата учителей государственных школ в трех географических регионах страны A. Если мы включим количественную Переменная, Расходы правительства штата на государственные школы на ученика, в этой регрессии мы получаем следующую модель:

Y_я = средняя годовая зарплата учителей государственных школ в штате i Икс_я = Государственные расходы на государственные школы на ученика D_2i = 1, если государство i находится в Северном регионе D_2i = 0, иначе D_3i = 1, если государство i находится в Южном регионе D_3i = 0, иначе

Скажем, выход регрессии для этой модели

Результат показывает, что на каждое увеличение государственных расходов на одного учащегося в государственных школах средняя зарплата учителя государственной школы увеличивается примерно на 3,29 доллара. Кроме того, для штата в Северном регионе средняя зарплата учителей ниже, чем в Западном регионе, примерно на 1673 доллара, а для штата в Южном регионе средняя заработная плата учителей ниже, чем в Западном регионе, примерно на 1144 долларов. На рисунке 3 схематически изображена эта модель. Строки средней заработной платы параллельны друг другу, исходя из предположения модели, что коэффициент расходов не зависит от штата. Компромисс, показанный отдельно на графике для каждой категории, находится между двумя количественными переменными: заработная плата учителей государственных школ (Y) по отношению к государственным расходам на ученика в государственных школах (X). [4]

Взаимодействия между фиктивными переменными

Количественные регрессоры в регрессионных моделях часто имеют взаимодействие между собой. Таким же образом качественные регрессоры или фиктивные переменные также могут иметь эффекты взаимодействия друг с другом, и эти взаимодействия могут быть отображены в регрессионной модели. Например, в регрессии, включающей определение заработной платы, если рассматривать две качественные переменные, а именно пол и семейное положение, может существовать взаимосвязь между семейным положением и полом. [6] Эти взаимодействия могут быть показаны в уравнении регрессии, как показано в приведенном ниже примере.

С двумя качественными переменными, являющимися полом и семейным положением, и с количественным объяснением, являющимся количеством лет образования, регрессия, которая является чисто линейной в объяснениях, будет

Эта спецификация не учитывает возможность того, что может иметь место взаимодействие между двумя качественными переменными, D₂ и D₃. Например, замужняя женщина может получать заработную плату, отличную от заработной платы не состоящего в браке мужчины, на сумму, не равную сумме разницы в том, что она единолично женщина и единолично состоит в браке. Тогда влияние взаимодействующих манекенов на среднее значение Y не просто добавка как в случае вышеприведенной спецификации, но мультипликативный также, и определение заработной платы может быть определено как:

β₂ = дифференциальный эффект женственности β₃ = дифференциальный эффект от брака β₄ = дальнейший дифференциальный эффект бытия обе женский и состоите в браке

Таким образом, макет взаимодействия (продукт двух макетов) может изменять зависимую переменную от значения, которое она получает, когда эти два макета рассматриваются по отдельности. [4]

D₄ = 1, если женщина незамужняя, 0 в противном случае D₅ = 1, если женатый мужчина, 0 в противном случае D₆ = 1, если замужняя женщина, 0 в противном случае

тогда достаточно указать регрессию

Тогда при нулевом шоковом члене значение зависимой переменной δ₁+ αX_я для базовой категории неженатых мужчин δ₁ + δ₄+ αX_я для незамужних женщин, δ₁ + δ₅+ αX_я для женатых мужчин, а δ₁ + δ₆+ αX_я для замужних женщин. Эта спецификация включает в себя такое же количество переменных с правой стороны, что и предыдущая спецификация с элементом взаимодействия, и результаты регрессии для прогнозируемого значения зависимой переменной, зависящей от X_ядля любой комбинации качественных признаков идентичны между данной спецификацией и спецификацией взаимодействия.

Фиктивные зависимые переменные

Например, решение работника стать частью рабочей силы становится фиктивной зависимой переменной. Решение дихотомический, то есть решение имеет два возможных исхода: да и нет. Таким образом, зависимая фиктивная переменная «Участие» примет значение 1, если участвует, и 0, если не участвует. [4] Некоторые другие примеры дихотомических зависимых манекенов цитируются ниже:

Решение: Выбор профессии. Зависимый манекен: Супервизор = 1, если супервизор, 0, если не супервизор.

Решение: Принадлежность к политической партии. Зависимый манекен: Принадлежность = 1, если связана с партией, 0, если не аффилирована.

Решение: Отставка. Зависимый манекен: На пенсии = 1, если на пенсии, 0, если не на пенсии.

Когда качественная зависимая фиктивная переменная имеет более двух значений (например, принадлежность ко многим политическим партиям), она становится множественным ответом, или мультиномиальной, или полихотомический модель. [8]

Модели зависимых фиктивных переменных

Линейная вероятностная модель

Обычная модель наименьших квадратов, в которой зависимая переменная Y дихотомический манекен, принимающий значения 0 и 1, является линейная вероятностная модель (LPM). [9] Предположим, мы рассматриваем следующую регрессию:

Модель LPM имеет ряд проблем:

Альтернативы LPM

Чтобы избежать ограничений LPM, необходима модель, которая в качестве объясняющей переменной Икс_я, увеличивается, п_я = E (Y_я = 1 | Икс_я) должен оставаться в диапазоне от 0 до 1. Таким образом, отношения между независимыми и зависимыми переменными обязательно нелинейны.

Для этого кумулятивная функция распределения (CDF) можно использовать для оценки регрессии зависимой фиктивной переменной. На рисунке 4 показана S-образная кривая, напоминающая CDF случайной величины. В этой модели вероятность находится между 0 и 1, и нелинейность была зафиксирована. Теперь стоит вопрос о выборе CDF, который будет использоваться.

Можно использовать два альтернативных CDF: логистика и нормальный CDF. Логистический CDF дает начало логит модель и нормальный CDF дает рост пробит модель. [4]

Логит модель

Недостатки LPM привели к разработке более совершенной и улучшенной модели, названной моделью logit. В логит-модели кумулятивное распределение члена ошибки в уравнении регрессии является логистическим. [9] Регрессия более реалистична, поскольку она нелинейна.

Эта связь показывает, что L_я линейно по отношению к Икс_я, но вероятности не линейны в терминах Икс_я. [10]

Пробит модель

Источник