Что такое csc в тригонометрии
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
13. Тригонометрические функции
В ядре Maple определены следующие тригонометрические функции:
Все эти функции являются периодическими (с периодом 2л, кроме тангенса и котангенса, у которых период равен л) и определены для действительного и комплексного аргументов. Примеры вычислений:
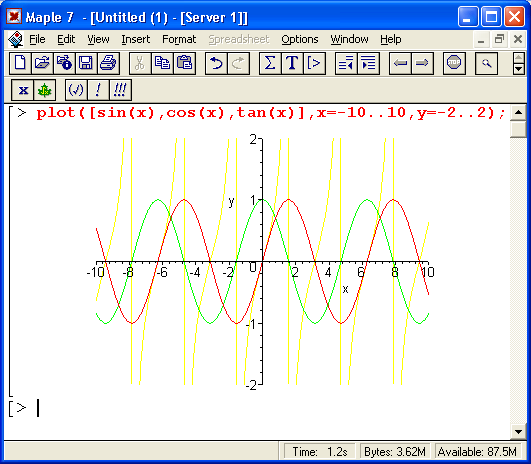
Многие свойства тригонометрических функций можно оценить, рассматривая их графики. Для построения таких графиков можно использовать функцию pi ot. На рис. 6.1 сверху показаны графики ряда тригонометрических функций.
Рис. 6.1. Графики ряда тригонометрических и обратных тригонометрических функций
Из графиков тригонометрических функций (рис. 6.1, сверху) хорошо видна их периодичность. Функция тангенса имеет разрывы, и ее значение в этих точках в пределе равно бесконечности. Поэтому для наглядного ее представления вместе с функциями синуса и косинуса (их экстремальные значения по модулю равны 1) приходится вводить ограничения на масштаб графика по оси у.
Обратите внимание на параметр color=black в функции построения графиков plot. Он задает построение всех графиков черным цветом, что сделано для более четкой печати их в книге. Если убрать этот параметр, то графики разных функций будут строиться с использованием разных цветов, что облегчит их различение. Другие способы выделения отдельных кривых будут описаны в дальнейшем при описании графических возможностей системы Maple 7.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Как сделать sin cos и tan на калькуляторе?
Найдите синус, косинус или тангенс угла. Просто введите значение угла в градусах и нажмите кнопку «без, »,« Cos »или« tan ». Преобразуйте синус угла в меру угла. Введите значение синуса, затем нажмите кнопку с надписью «arcsin» или «sin-1».
Следовательно, равен ли tan YX?
Определение единичного круга: tan (theta) = y / x или tan (theta) = sin (theta) / cos (theta). Функция тангенса отрицательна, если синус или косинус, но не оба, отрицательны: второй и четвертый квадранты. Касательная также равно наклон конечной стороны. … Как у синуса и косинуса.
Тогда что означает SOH CAH TOA?
Кроме того, в каком режиме должен быть мой калькулятор для sin и cos?
Для графических калькуляторов нажмите «Режим». » Если вы используете градусы (как правило, если вы занимаетесь геометрией), калькулятор должен быть установлен на градусы или «градусы». Если вы используете радианы (предварительное вычисление или тригонометрию), его следует установить в радианы или «рад». Нажмите кнопку «Cos», которая обычно находится в центре калькулятора.
Как узнать, когда использовать Sin Cos или загар?
Чему равна сек тета?
Чему равно sec?
Почему загар 30?
Можете ли вы использовать любой треугольник SOH CAH TOA?
В: Сохчатоа только для прямоугольных треугольников? А: Да, это относится только к прямоугольным треугольникам. … A: У прямоугольного треугольника гипотенуза всегда противоположна углу 90 градусов и является самой длинной стороной.
Как вы рассчитываете грех?
В любом прямоугольном треугольнике для любого угла:
Какова формула SOH CAH TOA?
| Так… | Синус = Противоположность / Гипотенуза |
|---|---|
| … Ну… | Косинус = Соседний / Гипотенуза |
| … Тоа | Касательная = напротив / рядом |
В каком режиме должен быть мой калькулятор?
Почти все калькуляторы поставляются с оба режима DEG и RAD. Вы должны использовать режим, который соответствует данным в вопросе. Например: если нам нужно найти cos (v) и v = 60 °, то используйте режим градусов, потому что данный угол выражен в градусах. Если заданный угол выражен в радианах, используйте режим RAD.
Как найти cos 1 на калькуляторе?
Как узнать, когда использовать режим в радианах или градусах?
Вы должны использовать радианы, когда вы смотрите на объекты, движущиеся по круговой траектории или части круговой траектории. В частности, уравнения вращательного движения почти всегда выражаются в радианах. Первоначальные параметры задачи могут быть в градусах, но вы должны преобразовать эти углы в радианы перед их использованием.
Какова длина стороны 30 60 90?
Размеры сторон x, x√3 и 2x. В треугольнике 30 ° –60 ° –90 ° длина гипотенузы в два раза больше длины более короткого плеча, а длина более длинного плеча в √3 раза больше длины более короткого плеча.
Как вы находите грех, данный Cos?
Основные два: синус и косинус
Каковы основы тригонометрии?
В тригонометрии есть три основные функции, каждая из которых является одной стороной прямоугольный треугольник разделен на другой. Возможно, вам будет полезно запомнить синус, косинус и тангенс как SOH CAH TOA.
Что такое формула тан-тета?
Что противоположно Cos?
секущий является обратной величиной косинуса. Это отношение гипотенузы к стороне, прилегающей к заданному углу в прямоугольном треугольнике.
Секунда противоположна Cos?
Секанс (сек ) (сек) (сек)
Секанс является обратной величиной косинуса. Это отношение гипотенузы к стороне, прилегающей к заданному углу в прямоугольном треугольнике.
Что такое сек на калькуляторе?
Описание. Секущая функция. SEC (x) возвращает секанс x. Аргумент x должен быть выражен в радианах.
Что означает детская кроватка в тригонометрии?
Прямоугольные определения треугольника
| функция | Аббревиатура | Описание |
|---|---|---|
| котангенс | детская кроватка (или котан или котг или ctg или ctn) | напротив |
| секущий | сек | гипотенуза |
| косеканс | csc (или cosec) | гипотенузапротивоположный |
Что такое детская кроватка 30 градусов?
Что такое косинус 30 градусов в дробной части?
Косинус угла 30 градусов в шестидесятеричной системе измерения углов записывается или выражается как cos (30 °). В дробном формате значение cos (30 °) равно √3 / 2.
Что такое CSC 30?
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.