Что такое броуновское движение диффузия кратко
Броуновское движение
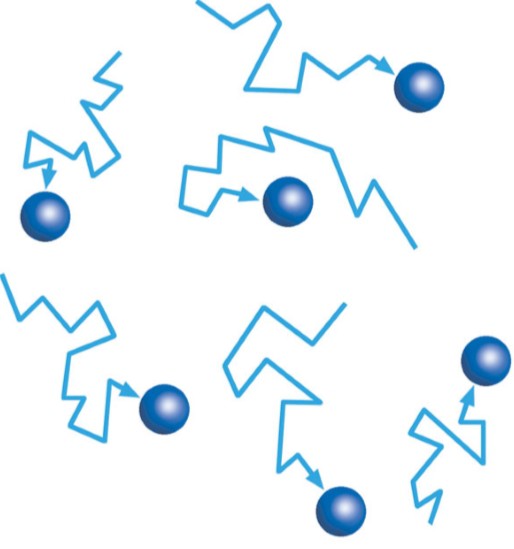
Броуновское движение — это беспорядочные перемещения малых частиц, возникающие вследствие их столкновения с невидимыми молекулами воды или газа. Первым его обнаружил ботаник Роберт Броун — частицы пыльцы, которые он разглядывал под микроскопом на мокром предметном стекле, двигались рывками, — однако описать математически смог только Альберт Эйнштейн. Броуновское движение объясняет, как распространяется в спокойном воздухе пыльца, но и описывает также множество случайных процессов — от наводнений до скачков на фондовом рынке. Его непредсказуемые рывки связаны с фракталами.
В XIX веке ботаник Роберт Броун, разглядывая под микроскопом частицы пыльцы, обнаружил, что они не стоят на месте, но отрывисто двигаются. На миг он задумался — уж не живые ли они? Нет, конечно, просто их сбивали с места молекулы воды, которой Броун смачивал предметные стекла. Частицы пыльцы двигались хаотично, иногда лишь немного, иногда на довольно большие расстояния, и, в конечном счете, совершали по стеклу путь, предсказать который было невозможно. И многие ученые начали задумываться над открытием Броуна, названным в его честь «броуновским движением».
Случайное блуждание
Броуновское движение совершается любыми малыми частицами, находящимися во взвешенном состоянии в жидкости или газе. Его можно наблюдать даже у довольно больших частиц, например частиц дыма, — при большом увеличении видно, какие зигзаги они описывают в воздухе. Сила получаемых частицами ударов зависит от импульса молекул. Она оказывается большей в случае тяжелых молекул жидкости либо газа — как и в случае быстро движущихся, например, молекул нагретой жидкости.
Во второй половине XIX века предпринималась не одна попытка описать броуновское движение математически, однако сделать это смог лишь Эйнштейн в 1905 году, когда он также опубликовал специальную теорию относительности и дал описание фотоэффекта, за что получил Нобелевскую премию. Эйнштейн воспользовался тепловой теорией, основанной на столкновениях молекул, и успешно объяснил движения частиц, которые наблюдал Броун. Поняв, что броуновское движение доказывает существование молекул жидкостей, физики вынуждены были принять и учение об атомах, которое даже в начале XX века еще вызывало сомнения.
Диффузия
Со временем броуновское движение способно заставить частицу пройти значительное расстояние, хоть, разумеется, и не такое, какое она могла бы пройти, если бы никто не мешал ей двигаться по прямой. Это объясняется случайным характером движения молекул, которые с равной вероятностью могут толкать ее и вперед, и назад. Поэтому, если уронить в жидкость плотную группу частиц, они начнут рассеиваться (диффундировать) во все стороны даже при том, что жидкость никто не будет помешивать и никакие потоки в ней не возникнут. Каждая частица пойдет по своему пути, и капля начнет расширяться, образуя диффузное облако. Такое рассеяние играет важную роль в распространении загрязнений воздуха, имеющих точечный источник, например в распространении аэрозоля в атмосфере. Даже при полном отсутствии ветра химические вещества будут рассеиваться в воздухе вследствие одного лишь броуновского движения.
Фракталы
Путь, по которому следует частица, совершающая броуновское движение, дает нам пример фрактала. Каждый прямой отрезок этого пути может иметь любую длину и любое направление, однако некоторый общий рисунок все же существует. Этот рисунок несет в себе определенную структуру, в каком масштабе его ни разглядывай — от наименьшего из вообразимых до очень больших. А это и есть определяющее свойство фрактала.
Фракталы были в 1960-х и 1970-х предложены Бенуа Мандельбротом как метод представления самоподобных фигур в количественной форме. Фракталы — это фигуры, которые при любом масштабе выглядят одинаково. Если увеличить малый кусочек этой фигуры, вы увидите точно такую же, неотличимую от первой, рассматриваемой в большем масштабе, поэтому определить степень увеличения, глядя на фигуру, ни за что не удастся. Такая безмасштабная повторяемость часто встречается в природе — в рисунке береговой линии, в ветвях дерева, в листьях папоротника, в шестикратной симметрии снежинки.
Фракталы отличаются тем, что их длина или размерность не зависят от того, с каким увеличением вы их рассматриваете. Если вы решите измерить расстояние между двумя приморскими городами, Лендс-Эндом и Маунтс-Беем, то, скорее всего, придете к выводу, что оно составляет 30 км, однако вспомните про все береговые скалы и попробуйте обвить каждую веревкой — и вы обнаружите, что веревка вам понадобится в сотню километров длиной. Если же вы пойдете еще дальше и затеете обмерять каждую песчинку берега, веревку придется удлинить до многих сотен километров. Выходит, что абсолютная длина береговой линии зависит от масштаба, в котором вы проводите измерения. Ограничьтесь грубым очертанием берега — и вы снова вернетесь к уже знакомым вам 30 км. В этом смысле фрактальная размерность есть мера огрубления чего-то, будь то облако, дерево или горный хребет. Многие из фрактальных форм, например береговую линию, можно получить соединением шагов случайного движения — отсюда и их связь с броуновским движением.
Математика броуновского движения, или последовательность случайных шагов, может использоваться для создания фрактальных фигур, находящих применение во многих областях науки. С ее помощью можно создавать грубо очерченные виртуальные пейзажи — горы, деревья, облака — компьютерных игр, ее можно использовать в программах пространственного картирования, которые помогают роботам двигаться по сильно пересеченной местности, моделируя ее возвышенности и низины. Врачи применяют ее для медицинской визуализации, когда у них возникает нужда проанализировать структуру сложных органов тела, скажем легких, в которых ветвящиеся структуры присутствуют во всех масштабах, от грубого до совсем малого.
Идеи броуновского движения используются и для предсказания рисков либо событий будущего, которые являются суммарным результатом множества случайных воздействий — наводнений, колебаний фондового рынка. Фондовый рынок можно рассматривать как портфель ценных бумаг, стоимость которых варьируется случайным образом, напоминая броуновское движение множества молекул. Фигурирует оно и в моделировании других социальных процессов, относящихся к производству товаров и принятию решений. Броуновское движение с его случайным характером обладает значительным влиянием и появляется во множестве обличий — не в одном только танце чаинок в чашке горячего чая.
Броуновское движение
Нам известно, что все вещества состоят из огромного числа очень и очень маленьких частиц, которые находятся в непрерывном и беспорядочном движении. Откуда нам это стало известно? Как учёные смогли узнать о существовании настолько маленьких частиц, которые ни в один оптический микроскоп невозможно увидеть? И уж тем более, как им удалось выяснить, что эти частицы находятся в непрерывном и беспорядочном движении? В этом учёным помогли разобраться два явления — броуновское движение и диффузия. Об этих явлениях мы и поговорим более подробно.
2. Броуновское движение
Английский учёный Роберт Броун не был физиком или химиком. Он был ботаником. И он совсем не ожидал, что откроет столь важное для физиков и химиков явление. И он не мог даже подозревать о том, что в своих довольно простых экспериментах он будет наблюдать результат хаотичного движения молекул. А это было именно так.
Что же это были за эксперименты? Они были почти такие же, что делают ученики на уроках биологии, когда с помощью микроскопа пытаются рассмотреть, например, клетки растений. Роберт Броун хотел рассмотреть в микроскоп пыльцу растений. Рассматривая зёрна пыльцы в капле воды, он заметил, что зёрна не находятся в покое, а непрерывно дёргаются, будто они живые. Наверное, сначала он так и подумал, но будучи учёным, конечно же отбросил эту мысль. Ему не удалось понять, почему эти зёрна пыльцы ведут себя таким странным образом, но он описал всё увиденное, и это описание попало в руки физиков, которые тут же поняли, что перед ними наглядное доказательство непрерывного и беспорядочного движения частиц.
Объясняется это движение, описанное Броуном, следующим образом: зёрна пыльцы достаточно велики, так что мы можем увидеть их в обычный микроскоп, а вот молекулы воды мы не видим, но, в то же время, зёрна пыльцы достаточно малы, чтобы из-за ударов по ним молекул воды, окружающих их со всех сторон, они смещались то в одну, то в другую сторону. То есть этот хаотичный «танец» зёрен пыльцы в капле воды показывал, что молекулы воды непрерывно и беспорядочно с разных сторон ударяют по зёрнам пыльцы и смещают их. С тех пор непрерывное и хаотичное движение мелких твёрдых частичек в жидкости или газе стали называть броуновским движением. Важнейшей особенностью этого движения является то, что оно непрерывное, то есть не прекращается никогда.
Диффузия — это ещё один пример наглядного доказательства непрерывного и беспорядочного движения молекул. И заключается оно в том, что газообразные вещества, жидкости и даже твёрдые вещества, хотя и намного медленнее, могут самоперемешиваться друг с другом. К примеру, запахи различных веществ распространяются в воздухе даже в отсутствие ветра именно благодаря этому самоперемешиванию. Или вот ещё пример — если в стакан с водой бросить несколько кристаллов марганцовки и, не перемешивая воду, подождать около суток, то мы увидим, что вся вода в стакане будет окрашена равномерно. Это происходит из-за непрерывного движения молекул, которые меняются местами, и вещества постепенно перемешиваются самостоятельно без внешнего воздействия.
4. Свойства броуновского движения и диффузии
Когда учёные-физики стали более подробно рассматривать явление, описанное Робертом Броуном, они заметили, что, как и диффузию, этот процесс можно ускорить, повышая температуру. То есть в горячей воде и окрашивание с помощью марганцовки будет происходить быстрее, и движение мелких твёрдых частичек, к примеру, графитовой крошки или тех же зёрен пыльцы, происходит с большей интенсивностью. Это подтверждало тот факт, что скорость хаотичного движения молекул напрямую зависит от температуры. Не вдаваясь в подробности, перечислим, от чего может зависеть и интенсивность броуновского движения, и скорость протекания диффузии:
2) от рода вещества, в котором эти процессы происходят;
3) от агрегатного состояния.
То есть при равной температуре диффузия газообразных веществ протекает значительно быстрее, чем жидкостей, не говоря уже о диффузии твёрдых тел, которая происходит настолько медленно, что её результат, и то очень незначительный, можно заметить или при очень высоких температурах, или за очень большое время — годы или даже десятилетия.
5. Практическое применение
Диффузия и без практического применения имеет огромное значение не только для человека, но и для всего живого на Земле: именно благодаря диффузии в нашу кровь через лёгкие попадает кислород, именно посредством диффузии растения добывают из почвы воду, поглощают углекислый газ из атмосферы и выделяют в ней кислород, а рыбы дышат в воде кислородом, который из атмосферы посредством диффузии попадает в воду.
Явление диффузии применяется и во многих областях техники, причём именно диффузии в твёрдых телах. К примеру, есть такой процесс — диффузионная сварка. В этом процессе детали очень сильно прижимаются друг к другу, нагреваются до 800 °C и посредством диффузии происходит их соединение друг с другом. Именно благодаря диффузии земная атмосфера, состоящая из большого количества различных газов, не разделяется на отдельные слои по составу, а везде примерно однородна — а ведь будь иначе, мы вряд ли смогли бы дышать.
Существует огромное количество примеров влияния диффузии на нашу жизнь и на всю природу, которые может найти любой из вас, если захочет. А вот о применении броуновского движения мало что можно сказать, кроме того, что сама теория, которая описывает это движение, может применяться и в других, казалось бы совершенно не связанных с физикой, явлениях. К примеру, эту теорию используют для описания случайных процессов, с применением большого количества данных и статистики — таких, как изменение цен. Теория броуновского движения используется для создания реалистичной компьютерной графики. Интересно, что человек, заблудившийся в лесу движется примерно так же, как и броуновские частички — блуждает из стороны в сторону, многократно пересекая свою траекторию.
6. Методические рекомендации учителям
1) Рассказывая классу о броуновском движении и диффузии, необходимо сделать акцент на том, что эти явления не доказывают факт существования молекул, но доказывают факт их движения и то, что оно беспорядочное — хаотичное.
2) Обязательно обратите особое внимание на то, что это непрерывное движение, зависящее от температуры, то есть тепловое движение, которое не может прекратиться никогда.
3) Продемонстрируйте диффузию с помощью воды и марганцовки, дав задание наиболее любознательным ребятам провести подобный эксперимент в домашних условиях и делая фотографии воды с марганцовкой через каждый час-два в течение дня (в выходной дети это с удовольствием сделают, а фото пришлют вам). Лучше, если в подобном эксперименте будет две ёмкости с водой — холодной и горячей, чтобы можно было продемонстрировать наглядно зависимость скорости диффузии от температуры.
4) Попробуйте измерить скорость диффузии в классе с помощью, к примеру, дезодоранта — в одном конце класса распыляем небольшое количество аэрозоля, а в 3-5 метрах от этого места ученик с секундомером фиксирует время, через которое он почувствует запах. Это и весело, и интересно, и запомнится детьми надолго!
5) Обсудите с детьми понятие хаотичности и тот факт, что даже в хаотических процессах учёные находят некие закономерности.
БРОУНОВСКОЕ ДВИЖЕНИЕ
БРОУНОВСКОЕ ДВИЖЕНИЕ – видимое в микроскоп хаотическое перемещение очень малых частиц вещества под действием ударов молекул. Названо в честь английского ученого Броуна (1773–1858).
Открытие Броуна.
Шотландский ботаник Роберт Броун (иногда его фамилию транскрибируют как Браун) еще при жизни как лучший знаток растений получил титул «князя ботаников». Он сделал много замечательных открытий. В 1805 после четырехлетней экспедиции в Австралию привез в Англию около 4000 видов не известных ученым австралийских растений и много лет потратил на их изучение. Описал растения, привезенные из Индонезии и Центральной Африки. Изучал физиологию растений, впервые подробно описал ядро растительной клетки. Петербургская Академия наук сделала его своим почетным членом. Но имя ученого сейчас широко известно вовсе не из-за этих работ.
В 1827 Броун проводил исследования пыльцы растений. Он, в частности, интересовался, как пыльца участвует в процессе оплодотворения. Как-то он разглядывал под микроскопом выделенные из клеток пыльцы североамериканского растения Clarkia pulchella (кларкии хорошенькой) взвешенные в воде удлиненные цитоплазматические зерна. Неожиданно Броун увидел, что мельчайшие твердые крупинки, которые едва можно было разглядеть в капле воды, непрерывно дрожат и передвигаются с места на место. Он установил, что эти движения, по его словам, «не связаны ни с потоками в жидкости, ни с ее постепенным испарением, а присущи самим частичкам».
Наблюдение Броуна подтвердили другие ученые. Мельчайшие частички вели себя, как живые, причем «танец» частиц ускорялся с повышением температуры и с уменьшением размера частиц и явно замедлялся при замене воды более вязкой средой. Это удивительное явление никогда не прекращалось: его можно было наблюдать сколь угодно долго. Поначалу Броун подумал даже, что в поле микроскопа действительно попали живые существа, тем более что пыльца – это мужские половые клетки растений, однако так же вели частички из мертвых растений, даже из засушенных за сто лет до этого в гербариях. Тогда Броун подумал, не есть ли это «элементарные молекулы живых существ», о которых говорил знаменитый французский естествоиспытатель Жорж Бюффон (1707–1788), автор 36-томной Естественной истории. Это предположение отпало, когда Броун начал исследовать явно неживые объекты; сначала это были очень мелкие частички угля, а также сажи и пыли лондонского воздуха, затем тонко растертые неорганические вещества: стекло, множество различных минералов. «Активные молекулы» оказались повсюду: «В каждом минерале, – писал Броун, – который мне удавалось измельчить в пыль до такой степени, чтобы она могла в течение какого-то времени быть взвешенной в воде, я находил, в больших или меньших количествах, эти молекулы».
Надо сказать, что у Броуна не было каких-то новейших микроскопов. В своей статье он специально подчеркивает, что у него были обычные двояковыпуклые линзы, которыми он пользовался в течение нескольких лет. И далее пишет: «В ходе всего исследования я продолжал использовать те же линзы, с которыми начал работу, чтобы придать больше убедительности моим утверждениям и чтобы сделать их как можно более доступными для обычных наблюдений».
Сейчас чтобы повторить наблюдение Броуна достаточно иметь не очень сильный микроскоп и рассмотреть с его помощью дым в зачерненной коробочке, освещенный через боковое отверстие лучом интенсивного света. В газе явление проявляется значительно ярче, чем в жидкости: видны рассеивающие свет маленькие клочки пепла или сажи (в зависимости от источника дыма), которые непрерывно скачут туда и сюда.
Как это часто бывает в науке, спустя многие годы историки обнаружили, что еще в 1670 изобретатель микроскопа голландец Антони Левенгук, видимо, наблюдал аналогичное явление, но редкость и несовершенство микроскопов, зачаточное состояние молекулярного учения в то время не привлекли внимания к наблюдению Левенгука, поэтому открытие справедливо приписывают Броуну, который впервые подробно его изучил и описал.
Броуновское движение и атомно-молекулярная теория.
Наблюдавшееся Броуном явление быстро стало широко известным. Он сам показывал свои опыты многочисленным коллегам (Броун перечисляет два десятка имен). Но объяснить это загадочное явление, которое назвали «броуновским движением», не смог ни сам Броун, ни многие другие ученые в течение многих лет. Перемещения частиц были совершенно беспорядочны: зарисовки их положения, сделанные в разные моменты времени (например, каждую минуту) не давали на первый взгляд никакой возможности найти в этих движениях какую-либо закономерность.
Объяснение броуновского движения (как назвали это явление) движением невидимых молекул было дано только в последней четверти 19 в., но далеко не сразу было принято всеми учеными. В 1863 преподаватель начертательной геометрии из Карлсруэ (Германия) Людвиг Кристиан Винер (1826–1896) предположил, что явление связано с колебательными движениями невидимых атомов. Это было первое, хотя и очень далекое от современного, объяснение броуновского движения свойствами самих атомов и молекул. Важно, что Винер увидел возможность с помощью этого явления проникнуть в тайны строения материи. Он впервые попытался измерить скорость перемещения броуновских частиц и ее зависимость от их размера. Любопытно, что в 1921 в Докладах Национальной Академии наук США была опубликована работа о броуновском движении другого Винера – Норберта, знаменитого основателя кибернетики.
Идеи Л.К.Винера были приняты и развиты рядом ученых – Зигмундом Экснером в Австрии (а спустя 33 года – и его сыном Феликсом), Джованни Кантони в Италии, Карлом Вильгельмом Негели в Германии, Луи Жоржем Гуи во Франции, тремя бельгийскими священниками-иезуитами Карбонелли, Дельсо и Тирьоном и другими. В числе этих ученых был и знаменитый впоследствии английский физик и химик Уильям Рамзай. Постепенно становилось понятным, что мельчайшие крупинки вещества испытывают со всех сторон удары еще более мелких частиц, которые в микроскоп уже не видны – как не видны с берега волны, качающие далекую лодку, тогда как движения самой лодки видны вполне отчетливо. Как писали в одной из статей 1877, «. закон больших чисел не сводит теперь эффект соударений к среднему равномерному давлению, их равнодействующая уже не будет равна нулю, а будет непрерывно изменять свое направление и свою величину».
Качественно картина была вполне правдоподобной и даже наглядной. Примерно так же должны перемещаться маленькая веточка или жучок, которых толкают (или тянут) в разные стороны множество муравьев. Эти более мелкие частицы на самом деле были в лексиконе ученых, только их никто никогда не видел. Называли их молекулами; в переводе с латинского это слово и означает «маленькая масса». Поразительно, но именно такое объяснение дал похожему явлению римский философ Тит Лукреций Кар (ок. 99–55 до н.э.) в своей знаменитой поэме О природе вещей. В ней мельчайшие невидимые глазом частицы он называет «первоначалами» вещей.
Первоначала вещей сначала движутся сами,
Следом за ними тела из мельчайшего их сочетанья,
Близкие, как бы сказать, по силам к началам первичным,
Скрыто от них получая толчки, начинают стремиться,
Сами к движенью затем побуждая тела покрупнее.
Так, исходя от начал, движение мало-помалу
Наших касается чувств, и становится видимым также
Нам и в пылинках оно, что движутся в солнечном свете,
Хоть незаметны толчки, от которых оно происходит.
Впоследствии оказалось, что Лукреций ошибался: невооруженным глазом наблюдать броуновское движение невозможно, а пылинки в солнечном луче, который проник в темную комнату, «пляшут» из-за вихревых движений воздуха. Но внешне оба явления имеют некоторое сходство. И только в 19 в. многим ученым стало очевидно, что движение броуновских частиц вызвано беспорядочными ударами молекул среды. Движущиеся молекулы наталкиваются на пылинки и другие твердые частицы, которые есть в воде. Чем выше температура, тем быстрее движение. Если пылинка велика, например, имеет размер 0,1 мм (диаметр в миллион раз больше, чем у молекулы воды), то множество одновременных ударов по ней со всех сторон взаимно уравновешиваются и она их практически не «чувствует» – примерно так же, как кусок дерева размером с тарелку не «почувствует» усилий множества муравьев, которые будут тянуть или толкать его в разные стороны. Если же пылинка сравнительно невелика, она под действием ударов окружающих молекул будет двигаться то в одну, то в другую сторону.
Броуновские частицы имеют размер порядка 0,1–1 мкм, т.е. от одной тысячной до одной десятитысячной доли миллиметра, потому-то Броуну и удалось разглядеть их перемещение, что он рассматривал крошечные цитоплазматические зернышки, а не саму пыльцу (о чем часто ошибочно пишут). Дело в том, что клетки пыльцы слишком большие. Так, у пыльцы луговых трав, которая переносится ветром и вызывает аллергические заболевания у людей (поллиноз), размер клеток обычно находится в пределах 20 – 50 мкм, т.е. они слишком велики для наблюдения броуновского движения. Важно отметить также, что отдельные передвижения броуновской частицы происходят очень часто и на очень малые расстояния, так что увидеть их невозможно, а под микроскопом видны перемещения, происшедшие за какой-то промежуток времени.
Казалось бы, сам факт существования броуновского движения однозначно доказывал молекулярное строение материи, однако даже в начале 20 в. были ученые, и в их числе – физики и химики, которые не верили в существование молекул. Атомно-молекулярная теория лишь медленно и с трудом завоевывала признание. Так, крупнейший французский химик-органик Марселен Бертло (1827–1907) писал: «Понятие молекулы, с точки зрения наших знаний, неопределенно, в то время как другое понятие – атом – чисто гипотетическое». Еще определеннее высказался известный французский химик А.Сент-Клер Девилль (1818–1881): «Я не допускаю ни закона Авогадро, ни атома, ни молекулы, ибо я отказываюсь верить в то, что не могу ни видеть, ни наблюдать». А немецкий физикохимик Вильгельм Оствальд (1853–1932), лауреат Нобелевской премии, один из основателей физической химии, еще в начале 20 в. решительно отрицал существование атомов. Он ухитрился написать трехтомный учебник химии, в котором слово «атом» ни разу даже не упоминается. Выступая 19 апреля 1904 с большим докладом в Королевском Институте перед членами английского Химического общества, Оствальд пытался доказать, что атомов не существует, а «то, что мы называем материей, является лишь совокупностью энергий, собранной воедино в данном месте».
Но даже те физики, которые принимали молекулярную теорию, не могли поверить, что таким простым способом доказывается справедливость атомно-молекулярного учения, поэтому выдвигались самые разнообразные альтернативные причины, чтобы объяснить явление. И это вполне в духе науки: пока причина какого-либо явления не выявлена однозначно, можно (и даже необходимо) предполагать различные гипотезы, которые следует по возможности проверять экспериментально или теоретически. Так, еще в 1905 в Энциклопедическом словаре Брокгауза и Ефрона была опубликована небольшая статья петербургского профессора физики Н.А.Гезехуса, учителя знаменитого академика А.Ф.Иоффе. Гезехус писал, что, по мнению некоторых ученых, броуновское движение вызывается «проходящими через жидкость световыми или тепловыми лучами», сводится к «простым потокам внутри жидкости, не имеющим ничего общего с движениями молекул», причем эти потоки могут вызываться «испарением, диффузией и другими причинами». Ведь уже было известно, что очень похожее движение пылинок в воздухе вызывается именно вихревыми потоками. Но объяснение, приведенное Гезехусом, легко можно было опровергнуть экспериментально: если в сильный микроскоп разглядывать две броуновские частички, находящиеся очень близко друг к другу, то их перемещения окажутся совершенно независимыми. Если бы эти движения вызывались какими-либо потоками в жидкости, то такие соседние частицы двигались бы согласованно.
Теория броуновского движения.
В начале 20 в. большинство ученых понимали молекулярную природу броуновского движения. Но все объяснения оставались чисто качественными, никакая количественная теория не выдерживала экспериментальной проверки. Кроме того, сами экспериментальные результаты были неотчетливы: фантастическое зрелище безостановочно мечущихся частиц гипнотизировало экспериментаторов, и какие именно характеристики явления нужно измерять, они не знали.
Несмотря на кажущийся полный беспорядок, случайные перемещения броуновских частиц оказалось все же возможным описать математической зависимостью. Впервые строгое объяснение броуновского движения дал в 1904 польский физик Мариан Смолуховский (1872–1917), который в те годы работал в Львовском университете. Одновременно теорию этого явления разрабатывал Альберт Эйнштейн (1879–1955), мало кому известный тогда эксперт 2-го класса в Патентном бюро швейцарского города Берна. Его статья, опубликованная в мае 1905 в немецком журнале Annalen der Physik, называлась О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты. Этим названием Эйнштейн хотел показать, что из молекулярно-кинетической теории строения материи с необходимостью вытекает существование случайного движения мельчайших твердых частиц в жидкостях.
Любопытно, что в самом начале этой статьи Эйнштейн пишет, что знаком с самим явлением, хотя и поверхностно: «Возможно, что рассматриваемые движения тождественны с так называемым броуновским молекулярным движением, однако доступные мне данные относительно последнего столь неточны, что я не мог составить об этом определенного мнения». А спустя десятки лет, уже на склоне жизни, Эйнштейн написал в свои воспоминаниях нечто иное – что вообще не знал о броуновском движении и фактически заново «открыл» его чисто теоретически: «Не зная, что наблюдения над „броуновским движением» давно известны, я открыл, что атомистическая теория приводит к существованию доступного наблюдению движения микроскопических взвешенных частиц». Как бы то ни было, а заканчивалась теоретическая статья Эйнштейна прямым призывом к экспериментаторам проверить его выводы на опыте: «Если бы какому-либо исследователю удалось вскоре ответить на поднятые здесь вопросы!» – таким необычным восклицанием заканчивает он свою статью.
Ответ на страстный призыв Эйнштейна не заставил себя долго ждать.
где R – газовая постоянная. Так, если за 1 мин частица диаметром 1 мкм сместится на 10 мкм, то за 9 мин – на 10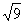
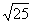
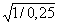
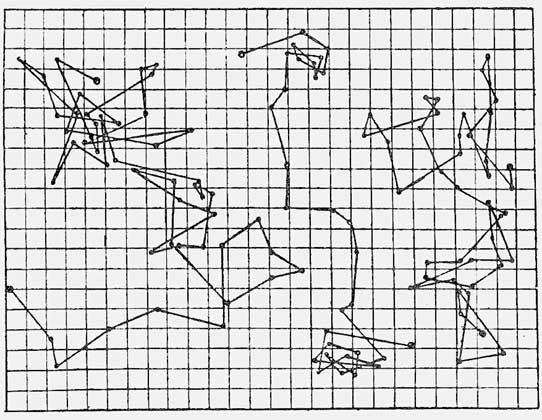
В 1908 Перрен начал количественные наблюдения за движением броуновских частиц под микроскопом. Он использовал изобретенный в 1902 ультрамикроскоп, который позволял обнаруживать мельчайшие частицы благодаря рассеянию на них света от мощного бокового осветителя. Крошечные шарики почти сферической формы и примерно одинакового размера Перрен получал из гуммигута – сгущенного сока некоторых тропических деревьев (он используется и как желтая акварельная краска). Эти крошечные шарики были взвешены в глицерине, содержащем 12% воды; вязкая жидкость препятствовала появлению в ней внутренних потоков, которые смазали бы картину. Вооружившись секундомером, Перрен отмечал и потом зарисовывал (конечно, в сильно увеличенном масштабе) на разграфленном листе бумаги положение частиц через равные интервалы, например, через каждые полминуты. Соединяя полученные точки прямыми, он получал замысловатые траектории, некоторые из них приведены на рисунке (они взяты из книги Перрена Атомы, опубликованной в 1920 в Париже). Такое хаотичное, беспорядочное движение частиц приводит к тому, что перемещаются они в пространстве довольно медленно: сумма отрезков намного больше смещения частицы от первой точки до последней.
Последовательные положения через каждые 30 секунд трех броуновских частиц – шариков гуммигута размером около 1 мкм. Одна клетка соответствует расстоянию 3 мкм. Если бы Перрен смог определять положение броуновских частиц не через 30, а через 3 секунды, то прямые между каждыми соседними точками превратились бы в такую же сложную зигзагообразную ломаную линию, только меньшего масштаба.
Результаты, полученные Перреном, подтвердили теоретические выводы Эйнштейна. Это произвело сильное впечатление. Как написал через много лет американский физик А.Пайс, «не перестаешь удивляться этому результату, полученному таким простым способом: достаточно приготовить взвесь шариков, размер которых велик по сравнению с размером простых молекул, взять секундомер и микроскоп, и можно определить постоянную Авогадро!» Можно удивляться и другому: до сих пор в научных журналах (Nature, Science, Journal of Chemical Education) время от времени появляются описания новых экспериментов по броуновскому движению! После публикации результатов Перрена бывший противник атомизма Оствальд признался, что «совпадение броуновского движения с требованиями кинетической гипотезы. дает теперь право самому осторожному ученому говорить об экспериментальном доказательстве атомистической теории материи. Таким образом, атомистическая теория возведена в ранг научной, прочно обоснованной теории». Ему вторит французский математик и физик Анри Пуанкаре: «Блестящее определение числа атомов Перреном завершило триумф атомизма. Атом химиков стал теперь реальностью».
Броуновское движение и диффузия.
Перемещение броуновских частиц внешне весьма напоминает перемещение отдельных молекул в результате их теплового движения. Такое перемещение называется диффузией. Еще до работ Смолуховского и Эйнштейна были установлены законы движения молекул в наиболее простом случае газообразного состояния вещества. Оказалось, что молекулы в газах движутся очень быстро – со скоростью пули, но далеко «улететь» не могут, так как очень часто сталкиваются с другими молекулами. Например, молекулы кислорода и азота в воздухе, двигаясь в среднем со скоростью примерно 500 м/с, испытывают каждую секунду более миллиарда столкновений. Поэтому путь молекулы, если бы могли за ним проследить, представлял бы собой сложную ломаную линию. Подобную же траекторию описывают и броуновские частицы, если фиксировать их положение через определенные промежутки времени. И диффузия, и броуновское движение являются следствием хаотичного теплового движения молекул и потому описываются сходными математическими зависимостями. Различие состоит в том, что молекулы в газах движутся по прямой, пока не столкнутся с другими молекулами, после чего меняют направление движения. Броуновская же частица никаких «свободных полетов», в отличие от молекулы, не совершает, а испытывает очень частые мелкие и нерегулярные «дрожания», в результате которых она хаотически смещается то в одну, то в другую сторону. Как показали расчеты, для частицы размером 0,1 мкм одно перемещение происходит за три миллиардные доли секунды на расстояние всего 0,5 нм (1 нм = 0,001 мкм). По меткому выражению одного автора, это напоминает перемещения пустой банки из-под пива на площади, где собралась толпа людей.
Диффузию наблюдать намного проще, чем броуновское движение, поскольку для этого не нужен микроскоп: наблюдаются перемещения не отдельных частиц, а огромной их массы, нужно только обеспечить, чтобы на диффузию не накладывалось конвекция – перемешивание вещества в результате вихревых потоков (такие потоки легко заметить, капнув каплю окрашенного раствора, например, чернил, в стакан с горячей водой).
Диффузию удобно наблюдать в густых гелях. Такой гель можно приготовить, например, в баночке из-под пенициллина, приготовив в ней 4–5%-ный раствор желатина. Желатин сначала должен несколько часов набухать, а затем его полностью растворяют при перемешивании, опустив баночку в горячую воду. После охлаждения получается нетекучий гель в виде прозрачной слегка мутноватой массы. Если с помощью острого пинцета осторожно ввести в центр этой массы небольшой кристаллик перманганата калия («марганцовки»), то кристаллик останется висеть в том месте, где его оставили, так как гель не дает ему упасть. Уже через несколько минут вокруг кристаллика начнет расти окрашенный в фиолетовый цвет шарик, со временем он становится все больше и больше, пока стенки баночки не исказят его форму. Такой же результат можно получить и с помощью кристаллика медного купороса, только в этом случае шарик получится не фиолетовым, а голубым.
Теория броуновского движения: случайные блуждания.
Теория Смолуховского – Эйнштейна объясняет закономерности и диффузии, и броуновского движения. Можно рассматривать эти закономерности на примере диффузии. Если скорость молекулы равна u, то, двигаясь по прямой, она за время t пройдет расстояние L = ut, но из-за столкновений с другими молекулами данная молекула не движется по прямой, а непрерывно изменяет направление своего движения. Если бы можно было зарисовать путь молекулы, он принципиально ничем бы не отличался от рисунков, полученных Перреном. Из таких рисунков видно, что из-за хаотичного движения молекула смещается на расстояние s, значительно меньшее, чем L. Эти величины связаны соотношением s =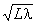
0,1 мкм, значит, при скорости 500 м/с молекула азота или кислорода пролетит за 10 000 секунд (меньше трех часов) расстояние L = 5000 км, а сместится от первоначального положения всего лишь на s = 0,7 м (70 см), поэтому вещества за счет диффузии передвигаются так медленно даже в газах.
Путь молекулы в результате диффузии (или путь броуновской частицы) называется случайным блужданием (по-английски random walk). Остряки-физики переиначили это выражение в drunkard’s walk – «путь пьяницы». Действительно, перемещение частицы от одного положения до другого (или путь молекулы, претерпевающей множество столкновений) напоминает движение нетрезвого человека. Более того, эта аналогия позволяет также довольно просто вывести основное уравнение такого процесса – на примере одномерного движения, которое легко обобщить на трехмерное. Делают это так.
Пусть подвыпивший матрос вышел поздно вечером из кабачка и направился вдоль улицы. Пройдя путь l до ближайшего фонаря, он отдохнул и пошел. либо дальше, до следующего фонаря, либо назад, к кабачку – ведь он не помнит, откуда пришел. Спрашивается, уйдет он когда-нибудь от кабачка, или так и будет бродить около него, то отдаляясь, то приближаясь к нему? (В другом варианте задачи говорится, что на обоих концах улицы, где кончаются фонари, находятся грязные канавы, и спрашивается, удастся ли матросу не свалиться в одну из них). Интуитивно кажется, что правилен второй ответ. Но он неверен: оказывается, матрос будет постепенно все более удаляться от нулевой точки, хотя и намного медленнее, чем если бы он шел только в одну сторону. Вот как это можно доказать.
Пройдя первый раз до ближайшего фонаря (вправо или влево), матрос окажется на расстоянии s1 = ± l от исходной точки. Так как нас интересует только его удаление от этой точки, но не направление, избавимся от знаков, возведя это выражение в квадрат: s1 2 = l 2. Спустя какое-то время, матрос, совершив уже N «блужданий», окажется на расстоянии
Так как s1 2 = l 2, то
Произведение u l в полученной формуле можно сопоставить с коэффициентом диффузии, который, как показал ирландский физик и математик Джордж Габриел Стокс (1819–1903), зависит от размера частицы и вязкости среды. На основании подобных соображений Эйнштейн и вывел свое уравнение.
Теория броуновского движения в реальной жизни.
Теория случайных блужданий имеет важное практическое приложение. Говорят, что в отсутствие ориентиров (солнце, звезды, шум шоссе или железной дороги и т.п.) человек бродит в лесу, по полю в буране или в густом тумане кругами, все время возвращаясь на прежнее место. На самом деле он ходит не кругами, а примерно так, как движутся молекулы или броуновские частицы. На прежнее место он вернуться может, но только случайно. А вот свой путь он пересекает много раз. Рассказывают также, что замерзших в пургу людей находили «в каком-нибудь километре» от ближайшего жилья или дороги, однако на самом деле у человека не было никаких шансов пройти этот километр, и вот почему.
Пусть теперь человек идет (вернее, блуждает) в лесу со скоростью 2 километра в час (для дороги это очень медленно, но для густого леса – очень быстро), тогда если величина l равна 20 метрам, то за час он пройдет 2 км, но сместится всего лишь на 200 м, за два часа – примерно на 280 м, за три часа – 350 м, за 4 часа – 400 м и т. д. А двигаясь по прямой с такой скоростью, человек за 4 часа прошел бы 8 километров, поэтому в инструкциях по технике безопасности полевых работ есть такое правило: если ориентиры потеряны, надо оставаться на месте, обустраивать убежище и ждать окончания ненастья (может выглянуть солнце) или помощи. В лесу же двигаться по прямой помогут ориентиры – деревья или кусты, причем каждый раз надо держаться двух таких ориентиров – одного спереди, другого сзади. Но, конечно, лучше всего брать с собой компас.