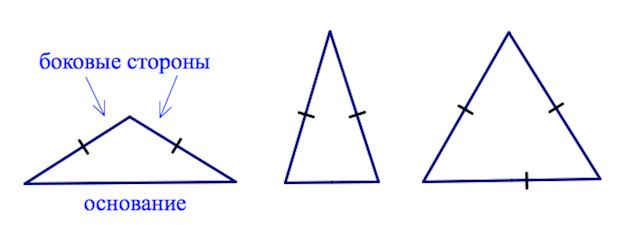
Что такое боковая сторона треугольника
Равнобедренный треугольник: свойства, признаки и формулы
Содержание:
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
Доказательство теоремы:
Вывод:
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
Доказательство теоремы:
Доказательство от противного.
Признаки равнобедренного треугольника
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
Формулы длины стороны (основания — b):
Формулы длины равных сторон — (а):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Площадь равнобедренного треугольника
Формула площади треугольника через высоту h и основание b, (S):
Равнобедренные треугольники
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Равнобедренный треугольник
Равнобедренный треугольник – треугольник, у которого две стороны равны между собой.
Свойства равнобедренного треугольника
1. Углы при основании равны
2. Биссектриса, медиана и высота, проведенные к основанию совпадают между собой
3. Углы при основании равнобедренного треугольника вычисляются по следующей формуле:
,
где – угол напротив основания.
4. Биссектрисы, медианы и высоты, проведённые из углов при основании равны между собой
5. Центры вписанной и описанной окружностей лежат на медиане=высоте=биссектрисе, проведенной к основанию
Признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то он равнобедренный.
2. Если в треугольнике медиана является и высотой (биссектрисой), то такой треугольник равнобедренный.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Боковая сторона равнобедренного треугольника

Всего получено оценок: 223.
Всего получено оценок: 223.
Боковая сторона равнобедренного треугольника достаточно интересное явление, поскольку ее часто просят найти в простых геометрических задач. Главное в нахождении боковой стороны знать основной метод решения, а сам процесс трудности не представляет.
Равнобедренный треугольник
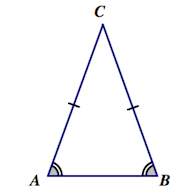
Равнобедренный треугольник – это треугольник, две стороны которого равны, а третья является основанием.
Только в равнобедренном треугольнике основание имеет реальное практическое применение. Для лучшего визуального восприятия фигуры стоит располагать чертеж так, чтобы основание располагалось снизу. При этом равносторонний треугольник считается частным случаем равнобедренного. В равностороннем треугольнике любая сторона может считаться как основанием, так и боковой. При этом равносторонний треугольник можно построить, зная только одну сторону. Построение равнобедренного треугольника по боковой стороне невозможно, нужно знать значение основания или угол между сторонами.
Свойства равнобедренного треугольника
Свойств равнобедренного треугольника не так много. В решениях школьных задач даже старших классов используется всего 3 свойства:
Этих свойств вполне достаточно, чтобы использовать стиль решения неприменимый для любого другого треугольника.
Боковая сторона треугольника
Равнобедренный отличается от остальных фигур тем, что достаточно двух показателей, из которых хотя бы один должен быть стороной, чтобы решить весь треугольник.
Если известно основание и любой из углов, то найти боковую сторону совсем не сложно. Если опустить на основание высоту, которая совпадет с медианой и биссектрисой, то получится два малых равных между собой прямоугольных треугольника, в которых боковая сторона будет являться гипотенузой.
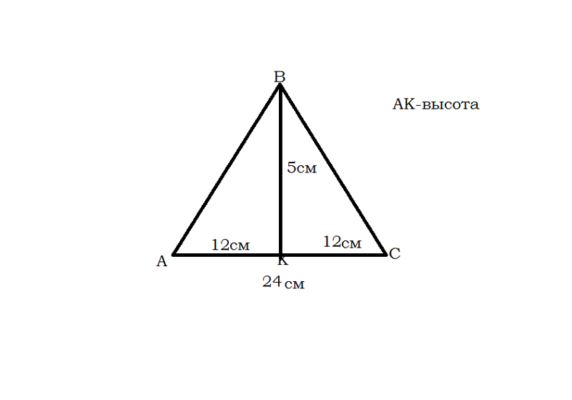
Сторону можно найти из тригонометрической функции синуса или косинуса. Выбор функции зависит от того, какой угол известен. Для этого понадобится один из катетов. Один из катетов является высотой и его найти не всегда возможно. Чаще всего используют катет, равный половине основания. А почему он равен половине основания?
Тригонометрическую функцию известного угла можно определить по таблицам Брадиса. В этих таблицах рассчитаны значения для всех существующих целых и промежуточных углов.
Равнобедренный треугольник нельзя решить, если:
Во всех остальных случаях треугольник можно решить, даже если известна только площадь и один из углов. Зачем знать варианты, когда решение точно невозможно? Чтобы не попасть в ловушку не решаемых задач. Такие редко, но встречаются. Предоставляя их к решению, составители проверяют уровень знаний учеников о фигуре.
Что мы узнали?
Мы поговорили о том, что такое равнобедренный треугольник, выделили основные его свойства и поговорили о методах нахождения сторон равнобедренного треугольника. Также мы выделили в отдельности боковую сторону и рассказали, как просто и быстро определить значение боковой стороны равнобедренного треугольника.
Боковая сторона равнобедренного треугольника – построение
Боковая сторона равнобедренного треугольника достаточно интересное явление, поскольку ее часто просят найти в простых геометрических задач. Главное в нахождении боковой стороны знать основной метод решения, а сам процесс трудности не представляет.
Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, две стороны которого равны, а третья является основанием.
Рис. 1. Равнобедренный треугольник
Только в равнобедренном треугольнике основание имеет реальное практическое применение. Для лучшего визуального восприятия фигуры стоит располагать чертеж так, чтобы основание располагалось снизу. При этом равносторонний треугольник считается частным случаем равнобедренного. В равностороннем треугольнике любая сторона может считаться как основанием, так и боковой. При этом равносторонний треугольник можно построить, зная только одну сторону. Построение равнобедренного треугольника по боковой стороне невозможно, нужно знать значение основания или угол между сторонами.
Рис. 2. Равносторонний треугольник
Свойства равнобедренного треугольника
Свойств равнобедренного треугольника не так много. В решениях школьных задач даже старших классов используется всего 3 свойства:
Этих свойств вполне достаточно, чтобы использовать стиль решения неприменимый для любого другого треугольника.
Боковая сторона треугольника
Равнобедренный отличается от остальных фигур тем, что достаточно двух показателей, из которых хотя бы один должен быть стороной, чтобы решить весь треугольник.
Если известно основание и любой из углов, то найти боковую сторону совсем не сложно. Если опустить на основание высоту, которая совпадет с медианой и биссектрисой, то получится два малых равных между собой прямоугольных треугольника, в которых боковая сторона будет являться гипотенузой.
Рис. 3. Высота равнобедренного треугольника
Сторону можно найти из тригонометрической функции синуса или косинуса. Выбор функции зависит от того, какой угол известен. Для этого понадобится один из катетов. Один из катетов является высотой и его найти не всегда возможно. Чаще всего используют катет, равный половине основания. А почему он равен половине основания?
Потому что основание делится проведенной высотой пополам, так как совпадает с медианой.
Вторая боковая сторона равна найденной. К слову, такой стиль решения применяется практически во всех задачах с равнобедренными треугольниками, поэтому стоит его запомнить.
Тригонометрическую функцию известного угла можно определить по таблицам Брадиса. В этих таблицах рассчитаны значения для всех существующих целых и промежуточных углов.
Равнобедренный треугольник нельзя решить, если:
Во всех остальных случаях треугольник можно решить, даже если известна только площадь и один из углов. Зачем знать варианты, когда решение точно невозможно? Чтобы не попасть в ловушку не решаемых задач. Такие редко, но встречаются. Предоставляя их к решению, составители проверяют уровень знаний учеников о фигуре.
Что мы узнали?
Мы поговорили о том, что такое равнобедренный треугольник, выделили основные его свойства и поговорили о методах нахождения сторон равнобедренного треугольника. Также мы выделили в отдельности боковую сторону и рассказали, как просто и быстро определить значение боковой стороны равнобедренного треугольника.