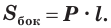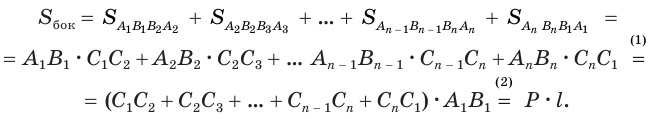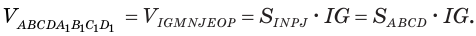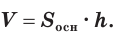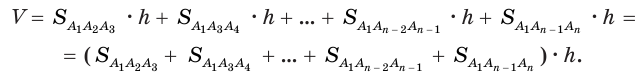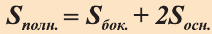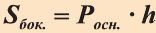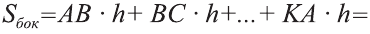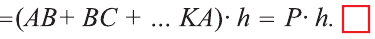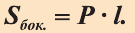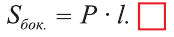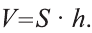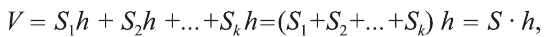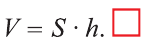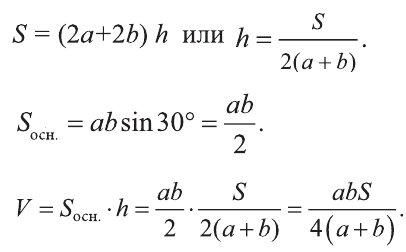Что такое боковая полная поверхность призмы
Инструменты пользователя
Инструменты сайта
Боковая панель
Стереометрия:
Контакты
Призма
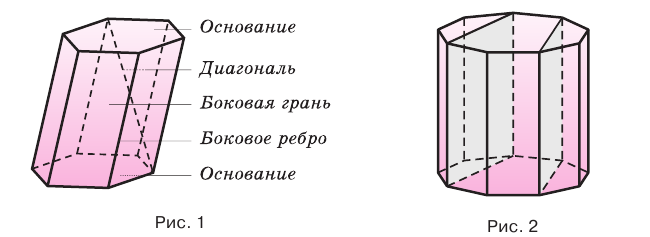
Призма — многогранник, две параллельные грани которого ( основания ) n−угольники, а остальные n граней ( боковые ) — параллелограммы. Очевидно, что все боковые ребра призмы равны, и в основаниях — равные n−угольники с соответственно параллельными сторонами.
Боковыми ребрами называются отрезки, соединяющие соответствующие вершины оснований.
Высотой призмы называется расстояние между плоскостями ее оснований.
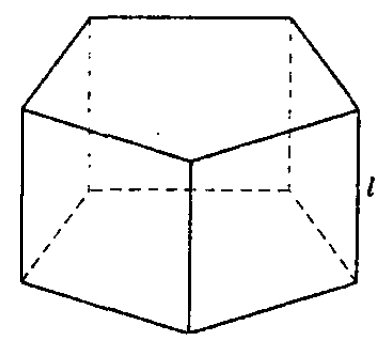
Призма называется прямой, если ее боковое ребро перпендикулярно плоскости основания. См.Рис.1
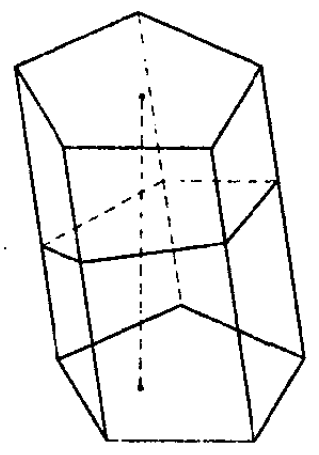
Призма называется наклонной, если боковое ребро призмы не перпендикулярно плоскости основания. См.Рис.2
Правильная призма — прямая призма, основания которой являютя правильными многоугольниками.
Площадь боковой поверхности призмы ( Sбок ) — сумма площадей её боковых граней.
Теорема о площади боковой поверхности прямой призмы. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Сечение, образованное плоскостью, перпендикулярной к боковому ребру призмы, называется нормальным (ортогональным) сечением призмы.
Призма называется параллелепипедом, если её основания — параллелограммы.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Перечень вопросов, рассматриваемых в теме:
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
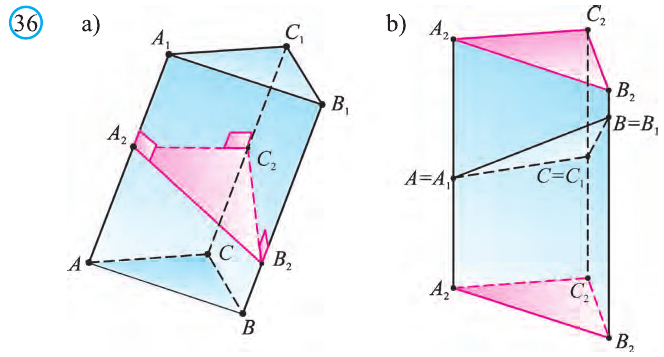
Определение призмы. Элементы призмы.
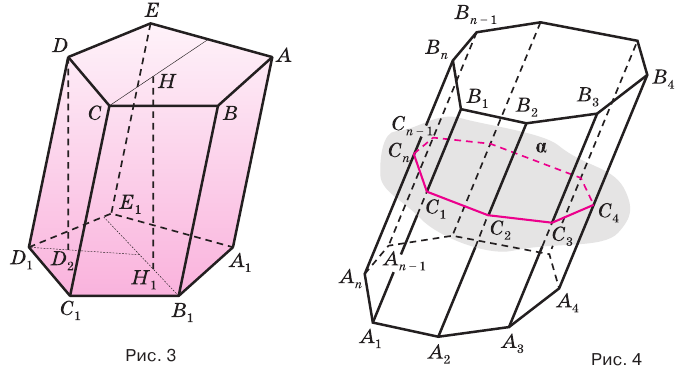
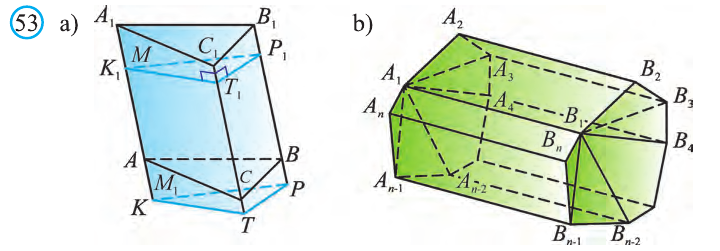
Рассмотрим два равных многоугольника А1А2. Аn и В1В2. Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2. АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).
Рисунок 2 – Наклонная призма
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
На рисунке 3 приведены примеры прямых призм
Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
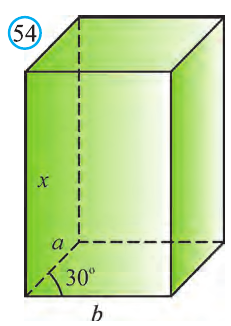
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
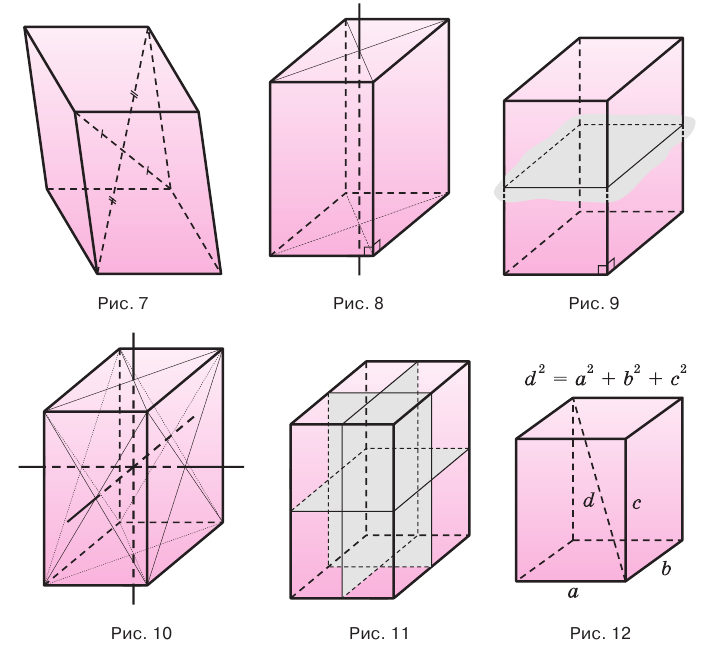
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.
Рисунок 4 – Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С 2 =АА1 2 +АС 2 (1).
Так как в основании прямоугольник, то ВС=АD.
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Найдите для каждой картинки пару
1)

4)
6)
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Объем призмы и другие ее характеристики
Перед вами иллюстрированный гид о призме.
В картинках. С пояснениями к формулам. С примерами.
Определение, виды призм, высота, площадь, объем призмы — все, все, все!
Читайте и делитесь впечатлениями в комментариях!
Призма — коротко о главном
Определение призмы:
Призма – это многогранник, две грани которого (основания) – равные многоугольники, лежащие в параллельных плоскостях, а боковые грани – параллелограммы.
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
Виды призм:
Параллелепипед — это призма, основанием которой является параллелограмм.
Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы – равные прямоугольники.
Объем призмы
Главная формула объема призмы:
\( \displaystyle V=S<<\ >_<основания>>\cdot \text\),
где \( <<\text>_<основания>>\) – площадь основания,
\( H\) – высота.
Необычная формула объема призмы:
\( \text=<<\text >_<\bot >>\cdot l\),
где \( <<\text>_<\bot >>\) – площадь сечения, перпендикулярного боковому ребру,
\( l\) – длина бокового ребра.
Площадь призмы
А теперь чуть подробнее…
Заходите и готовьтесь к ЕГЭ.
Что такое призма
Давай ответим сперва картинками:
Смотри: у призмы сверху и снизу два одинаковых многоугольника – они называются основаниями.
Остальные грани называются боковыми.
Плоскости оснований параллельный. Боковые грани – параллелограммы.
Смотри: бывают рёбра основания и боковые рёбра.
Все боковые рёбра призмы равны и параллельны.
Думаю, теперь мы можем дать более строгое определение призмы.
Определение призмы
Призма — многогранник, две грани которого (основания) — равные многоугольники, лежащие в параллельных плоскостях, а боковые грани — параллелограммы.
Виды призм
Призма, основанием которой является параллелограмм, называется параллелепипедом.
Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания.
Другие призмы называются наклонными.
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Высота призмы
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
И ясно, что та же самая высота получится, если опустить перпендикуляр из любой точки на верхней плоскости.
Объем призмы
Главная формула объема призмы
Необычная формула объема призмы
\( \text
=<<\text >_<\bot >>\cdot l\),
где \( <<\text>_<\bot >>\) — площадь сечения, перпендикулярного боковому ребру,
\( l\) — длина бокового ребра.
Площадь призмы
Прямая призма
Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.
Свойства прямой призмы:
Правильная призма
Если боковые рёбра призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, то призма называется правильной.
То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Тебе, скорее всего, может встретиться:
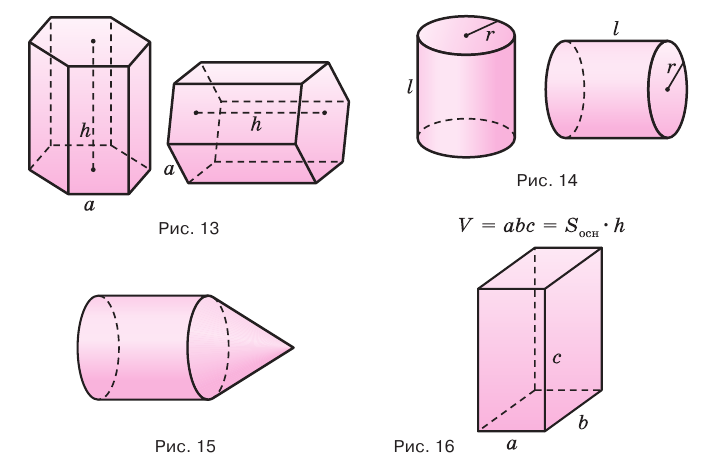
Правильная треугольная призма – в основании правильный треугольник, боковые грани – прямоугольники.
Правильная четырёхугольная призма – это ещё и разновидность прямоугольного параллелепипеда – в основании квадрат, боковые грани – прямоугольники.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
Главная формула объема призмы
Эта формула верна для любой призмы, но если призма прямая, то \( H\) «превращается» в боковое ребро. И тогда
\( \displaystyle V=S<<\ >_<основания>>\cdot боковое\ ребро\)
Необычная формула объёма призмы
Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы:
\( <<\text>_<\bot >>\) – площадь сечения, перпендикулярного боковому ребру,
\( l\) – длина бокового ребра
Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.
Давай теперь для упражнения посчитаем объём самых популярных призм.
Объем правильной треугольной призмы
Пусть дано, что сторона основания равна \( a\), а боковое ребро равно \( b\).
Вспомним, как находить площадь правильного треугольника:
Подставляем в формулу объёма:
Объем правильной четырёхугольной призмы
Опять дано: сторона основания равна \( a\), боковое ребро равно \( b\).
Ну, площадь квадрата долго искать не надо:
Объем правильной шестиугольной призмы
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Площадь поверхности призмы
Площадь боковой поверхности призмы – сумма площадей всех боковых граней.
Есть ли общая формула?
Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
Площадь полной поверхности призмы – сумма площадей всех граней.
Формулу можно написать для прямой призмы:
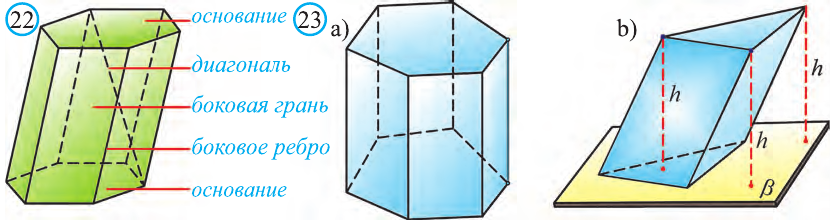
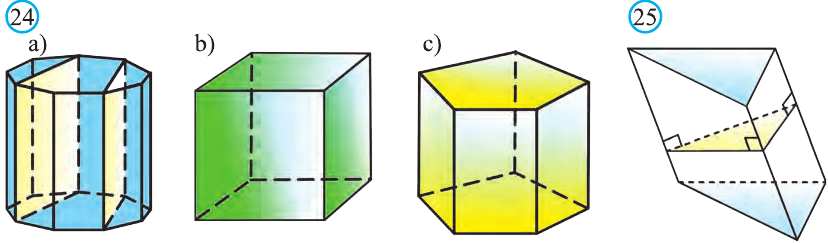
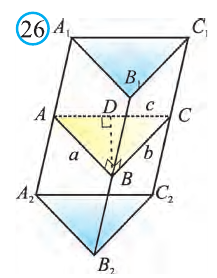
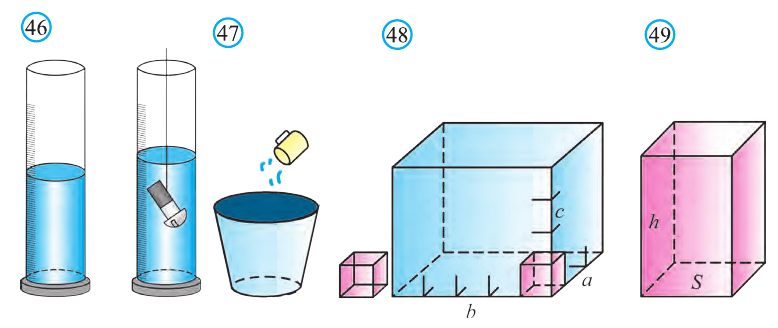
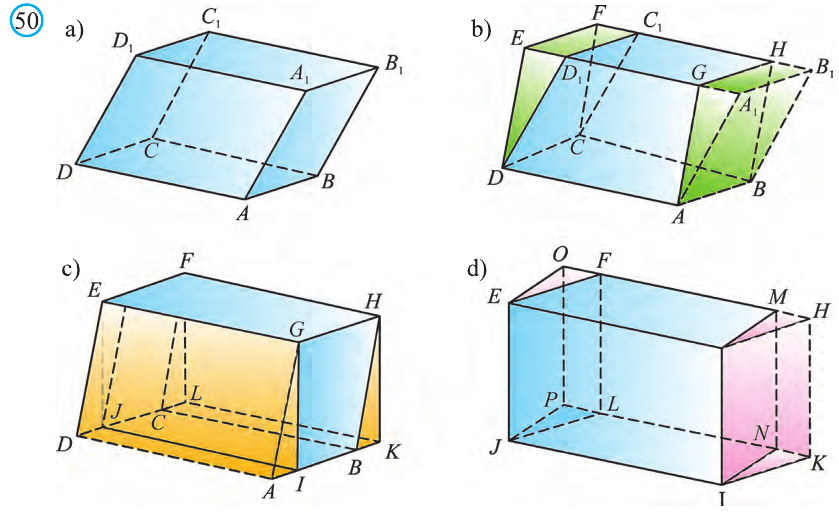
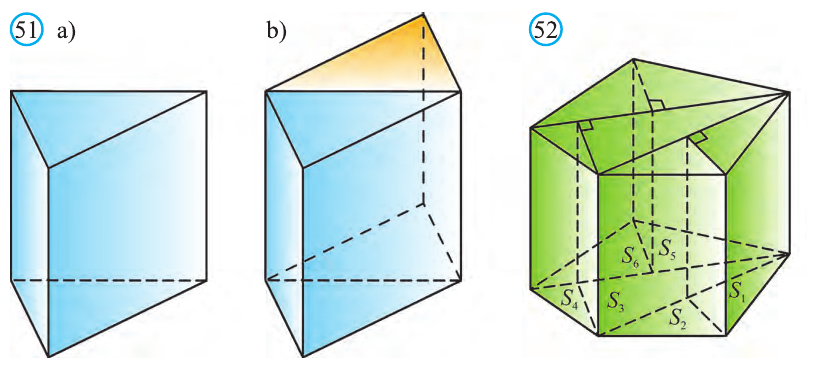
\( \displaystyle <<\text \), где \( \displaystyle P\) – периметр основания. Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы. Для примера посчитаем полную поверхность правильной шестиугольной призмы Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны. Многие ученики путают прямую и правильную призму. А ты теперь никогда не запутаешься! Была ли эта статья полезной? Ты все понял? Если у тебя остались вопросы, пиши внизу в комментариях! Разберёмся! Или если появились предложения. Или если просто хочешь поделиться своими мыслями. Мы будем очень рады. Тут всё понятно,впервые начинаю понимать стереометрию Супер Aper! Рады помочь! Когда читаю теорию этого учебника, такое ощущение, что я разговариваю с другом. Настолько все просто и приятно. Сказать, что я влюбилась в этот материал, ничего не сказать. Спасибо вам! Бася, вы нас растрогали таким комментарием. Спасибо большое! Удачи на экзамене! Некоторые комментарии прошлых лет об этой статье: Илья Дмитрий Regina Настя Женя Анна Жанна Николай Алексей Шевчук Содержание: Ранее вы уже знакомились с призмой, т. е. многогранником, две грани которого — равные Равные грани-многоугольники призмы лежат в параллельных плоскостях и называются основаниями призмы, а остальные грани-параллелограммы — боковыми гранями. Ребра боковых граней, не принадлежащие основаниям, называют боковыми ребрами. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называют диагональю призмы (рис. 1). Плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани, называется диагональной плоскостью, а сечение призмы диагональной плоскостью — диагональным сечением. На рисунке 2 показаны два диагональных сечения призмы. Призмы разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Призма, изображенная на рисунке 1, — шестиугольная, а на рисунке 2, — девятиугольная. Отличают прямые и наклонные призмы в зависимости от того, перпендикулярны или не перпендикулярны боковые ребра призмы ее основаниям. Обычно при изображении прямой призмы ее боковые ребра проводят вертикально. Прямая призма, основаниями которой являются правильные многоугольники, называется правильной призмой. В прямой призме все боковые грани — прямоугольники, а в правильной — равные прямоугольники. Перпендикуляр, проведенный из какой-либо точки одного основания призмы к плоскости другого основания, называется высотой призмы. На рисунке 3 показаны две высоты Боковые грани составляют боковую поверхность призмы, а боковые грани вместе с основаниями — полную поверхность призмы. Теорема 1. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра: Доказательство: Пусть имеется При переходе (1) мы учли, что все боковые ребра призмы равны друг другу, при переходе (2) — то, что сумма Следствие 1. Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты. Действительно, перпендикулярное сечение прямой призмы равно ее основанию, а боковое ребро является высотой. Частным видом призмы является параллелепипед, т. е. призма, основанием которой является параллелограмм. Параллелепипед, как и призма, может быть прямым или наклонным. Прямой параллелепипед, основаниями которого являются прямоугольники, называется прямоугольным параллелепипедом. Прямоугольный параллелепипед, у которого три ребра, выходящие из одной вершины, равны друг другу, называется кубом. У параллелепипеда все грани — параллелограммы, из которых у прямого параллелепипеда прямоугольниками являются боковые грани, а у прямоугольного параллелепипеда — все грани. 12 ребер параллелепипеда разделяются на три четверки равных ребер (рис. 5), его 6 граней — на три пары равных граней (рис. 6), а 4 диагонали пересекаются в одной точке, являющейся центром симметрии параллелепипеда (рис. 7). Прямой параллелепипед еще имеет ось симметрии (рис. 8) и плоскость симметрии (рис. 9). Прямоугольный параллелепипед имеет три оси симметрии (рис. 10) и три плоскости симметрии (рис. 11). Ребра прямоугольного параллелепипеда, выходящие из одной вершины, называют измерениями прямоугольного параллелепипеда. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (рис. 12), и все его диагонали равны друг другу. Важной характеристикой плоской фигуры является ее площадь. Подобной характеристикой тела является его объем. Будем считать, что изучаемые нами тела имеют объем. За единицу объема принимают объем куба с ребром 1. На практике пользуются разными единицами объема: как метрическими — кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр, кубический километр, так и неметрическими — галлон, барель, бушель, кварта. Для объема тела выполняются его основные свойства: При этом равными фигурами называют фигуры, которые преобразуются друг в друга определенным движением. Например, равными являются две шестиугольные правильные призмы, у которых соответственно равны стороны оснований и высоты (рис. 13), или два цилиндра с соответственно равными радиусами оснований и образующими (рис. 14). Тело, изображенное на рисунке 15, можно разделить на цилиндр и конус, и его объем равен сумме объемов этих цилиндра и конуса. Два тела с равными объемами называют равновеликими телами. Равные тела являются равновеликими, но не наоборот. Вы знаете, что объем Учитывая, что в формуле Теорема 2. Объем произвольного параллелепипеда равен произведению площади его основания и высоты: Доказательство: Пусть имеется произвольный параллелепипед У параллелепипеда Наконец, применив еще раз такое преобразование к граням Множитель Теорема 3. Объем призмы равен произведению площади ее основания и высоты: Доказательство: Рассмотрим сначала треугольную призму Объем параллелепипеда Отсюда следует, что объем призмы Учитывая, что сумма в скобках выражает площадь S основания данной призмы, получим: Следствие 2. Объем прямой призмы равен произведению площади ее основания и бокового ребра. С призмой вы уже знакомы. Несмотря на это, мы напомним определение призмы и её свойства. Если основания прямой призмы являются правильными многоугольниками, то её называют правильной (рис. 24). Боковые грани правильной призмы это равные между собой прямоугольники. Перпендикуляр, опущенный из некоторой точки одного основания к другому, называют его перпендикуляром (рис. 23.b). Сечение призмы, проходящее через соответствующие диагонали его оснований, называют диагональным сечением (рис. 24.а) и их число равно числу диагоналей одного из оснований. Перпендикулярным сечением призмы называют сечение перпендикулярное всем его боковым рёбрам (рис. 25). так как В каждом диагональном сечении призмы можно провести две диагонали. Следовательно, n-угольная призма имеет Пример: В наклонной треугольной призме расстояния между боковыми ребрами соответственно равны 7 см, 15 см и 20 см. Найдите расстояние между большей боковой гранью и противолежащим боковым ребром. Решение: Известно, что расстояние между параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки одной прямой на другую. Тогда длины сторон перпендикулярного сечения ABC (рис. 26). Наибольшая грань призмы проходит через наибольшую сторону АС= 20 см этого сечения. Расстояние от рёбра призмы В2В1 до плоскости грани Тогда по формуле Герона получаем: С другой стороны, Отсюда Ответ: 4,2 см. Призма, основаниями которой являются параллелограммы, называют параллелепипедом (рис. 27). Параллелепипеды также как и призмы могут быть прямыми (рис. 27.а) и наклонными (рис. 27.b). Грани параллелепипеда, не имеющие общую вершину, называют противоположными гранями. Прямой параллелепипед, основания которого являются прямоугольники, называют прямоугольным параллелепипедом (рис. 29). Очевидно, что все грани прямоугольного параллелепипеда являются прямоугольниками. Прямоугольный параллелепипед имеет три оси симметрии (рис. 30) и три плоскости симметрии (рис. 31). Длины трех рёбер, исходящих из одной вершины прямоугольного параллелепипеда называют его измерениями. Свойство: В прямоугольном параллелепипеде квадрат любой диагонали d равен сумме квадратов его измерений: а, b и с (рис.32): Прямоугольный параллелепипед, все измерения которого равны, называют кубом. Очевидно, что все грани куба являются равными квадратами. Куб имеет один центр симметрии, 9 осей симметрии и 9 плоскостей симметрии. Выше были перечислены свойства призмы. Некоторые из них были показаны в 10 классе. Доказательства остальных свойств проще, поэтому их доказательства вы можете провести самостоятельно. На рисунке 33 проведены высоты НН1 DD1 призмы АВСDЕ—А1В1С1D1Е1. Очевидно, что высоты правильной призмы будут равны её боковому рёбру. Боковая поверхность призмы (точнее, площадь боковой поверхности)равна сумме боковых поверхностей ее граней, а полная поверхнасть равна сумме боковой поверхности и площадей двух ее оснований. Теорема. Боковая поверхность прямой призмы равна произведению периметра ее основания на высоту: Доказательство. Пусть высота данной прямой призмы равна Тогда Теорема. Боковая поверхность произвольной призмы равна произведению периметра перпендикулярного сечения призмы на ее боковое ребро: Доказательство. Пусть периметр перпендикулярного сечения призмы равен Р (рис. 35). Сечение делит призму на две части (рис. 36.а). Совершим параллельный перенос одной из этих частей так, чтобы основания нашей призмы совпали. В результате мы получим новую прямую призму (рис. 36.b). Очевидно, что, боковая поверхность этой призмы равна боковой поверхности данной. Её основанием является перпендикулярное сечение, а боковое ребро равно Тогда по доказанной выше теореме: Одним из свойств, характеризующих геометрические тела в пространстве, является понятие объема. Каждый предмет (тело) занимает некоторую часть пространства. Например, кирпич по сравнению со спичечным коробком занимает большую часть пространства. Для сравнения этих частей между собой вводится понятие объёма. Объёмы тел измеряют различными способами или вычисляют. Например, объёмы маленьких предметов можно измерить с помощью сосудов (мензурки) с мелкими делениями (шкалами) (рис. 46). А объём ведра можно измерить с помощью сосуда, имеющего единичный объём, наполнив его водой (рис. 47). Но таким способом мы не можем измерить объёмы всех тел. В таких случаях объём вычисляют различными способами. Ниже рассмотрим их без доказательств. Теорема. Объём прямоугольного параллелепипеда равен произведению трех его измерeний (рис.48): Следствие. Объём прямоугольного параллелепипеда равен произведению площади его основания на высоту (рис. 49): Теорема. Объём произвольного параллелепипеда равен произведению площади его основания на высоту (рис. 50): Это свойство вытекает из вышеупомянутого следствия. На рисунке 50 показано как данный параллелепипед преобразовать в прямоугольный параллелепипед. Воспользовавшись этим самостоятельно обоснуйте свойство. Теорема. Объём прямой призмы равен произведению площади его основания на высоту (рис. 51): Если объём данной призмы, площадь её основания и высота V, S и h, то объём полученного прямоугольного параллелепипеда, площадь его основания и высота будут соответственно равны 2V, 2S и h. Следовательно Объём данной призмы равен сумме объёмов составляющих её треугольных призм: или Теорема. Объём произвольной призмы равен произведению площади его основания на высоту: По рисунку 5.3 докажите эту теорему самостоятельно, сначала для треугольной призмы (рис. 5.3.а), затем для любой призмы (рис. 5.3.b). Стороны основания прямого параллелепипеда равны а и b, а угол между ними 30°. Найдите его объём, если площадь его боковой поверхности равна S. Решение: Обозначим высоту параллелепипеда h(рис. 54). Тогда по условию задачи: При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.>_<боков.>>=\textЧитать далее…
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
А теперь мы хотим узнать твое мнение!
Добавить комментарий Отменить ответ
5 комментариев
26 ноября 2017
Огромное вам спасибо за созданный сайт, он очень удобен и информативен. Мне сложно представить какое количество времени было потрачено на «переработку» материала в понятном и доступном виде.Теперь есть источник чистых знаний, без лишней «воды», который не только помогает узнать новое, но и систематизировать информацию в голове. Жаль, что я не нашел сайт раньше. Вы лучшие!
21 февраля 2018
Сайт отличный!Все подробно описано. Никогда не понимал эту тему, но благодаря создателям этого сайта я наконец понял эту тему. Спасибо вам за ваши труды. Очень вам благодарен.
29 марта 2018
Аааааааа,это просто лучшее. Никогда не разбиралась в геометрии…Готовясь к зачету искала все сайты на эту тему. Нашла вас. Ввы все объяснили просто и доступно. Спасибо большое!
21 мая 2018
Красивый сайт, ничего глаза не режет, смотреть и читать приятно.
27 февраля 2019
можете указать свои инициалы? мне это для проекта надо)
29 апреля 2019
Преподнесено очень понятным языком, с наглядными картинками, спасибо) Хотелось бы хоть пример одной задачи и решение чтобы было открыто бесплатно, чтобы понять на сколько хорошо поясняете, но я думаю все ок.
27 апреля 2020
Спасибо! Я — учитель и мне очень понравилось!
04 июня 2020
Все очень доступно и понятно. Только вот не написано в статье про диагональ призмы. А так все просто супер, подготовился к сессии по данному материалу 🙂
05 июня 2020
Николай, спасибо. Диагонали в разных призмах разные, а в треугольной её и вовсе нет, поэтому длина диагонали — частный случай, а не какая-то полезная формула. Стоит рассмотрения разве что диагональ прямоугольного параллелепипеда — она вычисляется по теореме Пифагора и равна корню из суммы квадратов рёбер.Что такое призма
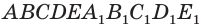
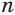
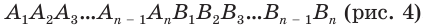
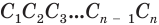
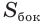

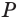
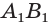
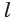
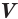
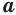
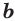
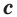
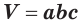
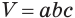
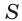
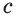
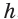
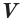

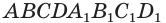
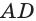
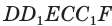
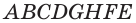
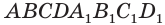
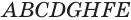
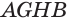

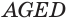
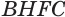

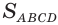
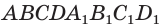
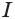
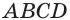
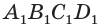
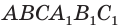
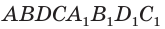
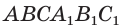
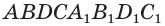
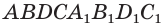
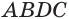
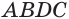
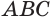
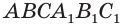
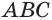
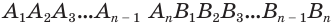
Призма и её сечения
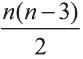
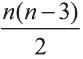
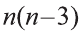
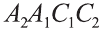
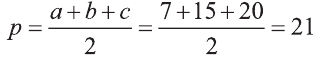
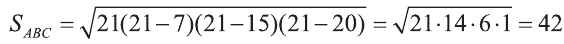
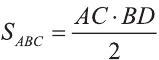
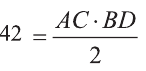
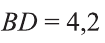
Параллелепипед и куб
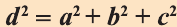
Площади боковой и полной поверхности призмы
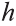
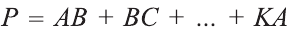
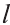
Объем призмы
Объём параллелепипеда
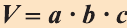
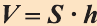
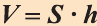
Нахождение объёма призмы
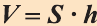
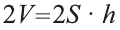
Пример: