Что такое биноминальное распределение
Биномиальное распределение случайной величины
Не все явления измеряются в количественной шкале типа 1, 2, 3 … 100500 … Не всегда явление может принимать бесконечное или большое количество различных состояний. Например, пол у человека может быть либо М, либо Ж. Стрелок либо попадает в цель, либо не попадает. Голосовать можно либо «За», либо «Против» и т.д. и т.п. Другими словами, такие данные отражают состояние альтернативного признака – либо «да» (событие наступило), либо «нет» (событие не наступило). Наступившее событие (положительный исход) еще называют «успехом».
Эксперименты с такими данными называются схемой Бернулли, в честь известного швейцарского математика, который установил, что при большом количестве испытаний соотношение положительных исходов и общего количества испытаний стремится к вероятности наступления этого события.
Переменная альтернативного признака
Для того, чтобы в анализе задействовать математический аппарат, результаты подобных наблюдений следует записать в числовом виде. Для этого положительному исходу присваивают число 1, отрицательному – 0. Другими словами, мы имеем дело с переменной, которая может принимать только два значения: 0 или 1.
Какую пользу отсюда можно извлечь? Вообще-то не меньшую, чем от обычных данных. Так, легко подсчитать количество положительных исходов – достаточно просуммировать все значения, т.е. все 1 (успехи). Можно пойти далее, но для этого потребуется ввести парочку обозначений.
Первым делом нужно отметить, что положительные исходы (которые равны 1) имеют некоторую вероятность появления. Например, выпадение орла при подбрасывании монеты равно ½ или 0,5. Такая вероятность традиционно обозначается латинской буквой p. Следовательно, вероятность наступления альтернативного события равна 1 — p, которую еще обозначают через q, то есть q = 1 – p. Указанные обозначения можно наглядно систематизировать в виде таблички распределения переменной X.
Мы получили перечень возможных значений и их вероятности. Можно рассчитать математическое ожидание и дисперсию. Матожидание – это сумма произведений всех возможных значений на соответствующие им вероятности:
Вычислим матожидание, используя обозначения в таблицы выше.
Получается, что математическое ожидание альтернативного признака равно вероятности этого события – p.
Теперь определим, что такое дисперсия альтернативного признака. Дисперсия – есть средний квадрат отклонений от математического ожидания. Общая формула (для дискретных данных) имеет вид:
Отсюда дисперсия альтернативного признака:
Нетрудно заметить, что эта дисперсия имеет максимум 0,25 (при p=0,5).
Стандартное отклонение – корень из дисперсии:
Максимальное значение не превышает 0,5.
Как видно, и математическое ожидание, и дисперсия альтернативного признака имеют очень компактный вид.
Биномиальное распределение случайной величины
Рассмотрим ситуацию под другим углом. Действительно, кому интересно, что среднее выпадение орлов при одном бросании равно 0,5? Это даже невозможно представить. Интересней поставить вопрос о числе выпадения орлов при заданном количестве бросков.
Другими словами, исследователя часто интересует вероятность наступления некоторого числа успешных событий. Это может быть количество бракованных изделий в проверяемой партии (1- бракованная, 0 — годная) или количество выздоровлений (1 – здоров, 0 – больной) и т.д. Количество таких «успехов» будет равно сумме всех значений переменной X, т.е. количеству единичных исходов.
Случайная величина B называется биномиальной и принимает значения от 0 до n (при B = 0 – все детали годные, при B = n – все детали бракованные). Предполагается, что все значения x независимы между собой. Рассмотрим основные характеристики биномиальной переменной, то есть установим ее математическое ожидание, дисперсию и распределение.
Матожидание биномиальной переменной получить очень легко. Математическое ожидание суммы величин есть сумма математических ожиданий каждой складываемой величины, а оно у всех одинаковое, поэтому:
Например, математическое ожидание количества выпавших орлов при 100 подбрасываниях равно 100 × 0,5 = 50.
Теперь выведем формулу дисперсии биномиальной переменной. Дисперсия суммы независимых случайных величин есть сумма дисперсий. Отсюда
Стандартное отклонение, соответственно
Для 100 подбрасываний монеты стандартное отклонение количества орлов равно
И, наконец, рассмотрим распределение биномиальной величины, т.е. вероятности того, что случайная величина B будет принимать различные значения k, где 0≤ k ≤n. Для монеты эта задача может звучать так: какова вероятность выпадения 40 орлов при 100 бросках?
Чтобы понять метод расчета, представим, что монета подбрасывается всего 4 раза. Каждый раз может выпасть любая из сторон. Мы задаемся вопросом: какова вероятность выпадения 2 орлов из 4 бросков. Каждый бросок независим друг от друга. Значит, вероятность выпадения какой-либо комбинации будет равна произведению вероятностей заданного исхода для каждого отдельного броска. Пусть О – это орел, Р – решка. Тогда, к примеру, одна из устраивающих нас комбинаций может выглядеть как ООРР, то есть:
Вероятность такой комбинации равняется произведению двух вероятностей выпадения орла и еще двух вероятностей не выпадения орла (обратное событие, рассчитываемое как 1 — p), т.е. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Такова вероятность одной из устраивающих нас комбинации. Но вопрос ведь стоял об общем количестве орлов, а не о каком-то определенном порядке. Тогда нужно сложить вероятности всех комбинаций, в которых присутствует ровно 2 орла. Ясно, все они одинаковы (от перемены мест множителей произведение не меняется). Поэтому нужно вычислить их количество, а затем умножить на вероятность любой такой комбинации. Подсчитаем все варианты сочетаний из 4 бросков по 2 орла: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР. Всего 6 вариантов.
Следовательно, искомая вероятность выпадения 2 орлов после 4 бросков равна 6×0,0625=0,375.
Однако подсчет подобным образом утомителен. Уже для 10 монет методом перебора получить общее количество вариантов будет очень трудно. Поэтому умные люди давно изобрели формулу, с помощью которой рассчитывают количество различных сочетаний из n элементов по k, где n – общее количество элементов, k – количество элементов, варианты расположения которых и подсчитываются. Формула сочетания из n элементов по k такова:
Подобные вещи проходят в разделе комбинаторики. Всех желающих подтянуть знания отправляю туда. Отсюда, кстати, и название биномиального распределения (формула выше является коэффициентом в разложении бинома Ньютона).
Формулу для определения вероятности легко обобщить на любое количество n и k. В итоге формула биномиального распределения имеет следующий вид.
Количество подходящих под условие комбинаций умножить на вероятность одной из них.
Для практического использования достаточно просто знать формулу биномиального распределения. А можно даже и не знать – ниже показано, как определить вероятность с помощью Excel. Но лучше все-таки знать.
Рассчитаем по этой формуле вероятность выпадения 40 орлов при 100 бросках:
Или всего 1,08%. Для сравнения вероятность наступления математического ожидания этого эксперимента, то есть 50 орлов, равна 7,96%. Максимальная вероятность биномиальной величины принадлежит значению, соответствующему математическому ожиданию.
Расчет вероятностей биномиального распределения в Excel
Если использовать только бумагу и калькулятор, то расчеты по формуле биномиального распределения, несмотря на отсутствие интегралов, даются довольно тяжело. К примеру значение 100! – имеет более 150 знаков. Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы. В настоящий момент целесообразно использовать специальное ПО, типа MS Excel. Таким образом, любой пользователь (даже гуманитарий по образованию) вполне может вычислить вероятность значения биномиально распределенной случайной величины.
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов. Ниже приведена картинка с этапами вычислений и конечным результатом.
Как видно, промежуточные результаты имеют такой масштаб, что не помещаются в ячейку, хотя везде и используются простые функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления. Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек. Да и разобраться с ходу трудновато.
В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМ.РАСП.
Синтаксис функции состоит из 4 аргументов:
Поля имеют следующие назначения:
Число успехов – количество успешных испытаний. У нас их 50.
Число испытаний – количество бросков: 100 раз.
Вероятность успеха – вероятность выпадения орла при одном подбрасывании 0,5.
Интегральная – указывается либо 1, либо 0. Если 0, то рассчитается вероятность P(B=k); если 1, то рассчитается функция биномиального распределения, т.е. сумма всех вероятностей от B=0 до B=k включительно.
Нажимаем ОК и получаем тот же результат, что и выше, только все рассчиталось одной функцией.
Очень удобно. Эксперимента ради вместо последнего параметра 0 поставим 1. Получим 0,5398. Это значит, что при 100 подкидываниях монеты вероятность выпадения орлов в количестве от 0 до 50 равна почти 54%. А поначалу то казалось, что должно быть 50%. В общем, расчеты производятся легко и быстро.
Настоящий аналитик должен понимать, как ведет себя функция (каково ее распределение), поэтому произведем расчет вероятностей для всех значений от 0 до 100. То есть зададимся вопросом: какова вероятность, что не выпадет ни одного орла, что выпадет 1 орел, 2, 3, 50, 90 или 100. Расчет приведен в следующей картинке. Синяя линия – само биномиальное распределение, красная точка – вероятность для конкретного числа успехов k.
Кто-то может спросить, а не похоже ли биномиальное распределение на… Да, очень похоже. Еще Муавр (в 1733 г.) говорил, что биномиальное распределение при больших выборках приближается к нормальному закону (не знаю, как это тогда называлось), но его никто не слушал. Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается. Также, как и у нормального закона.
Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро.
Биноминальное распределение
В настоящей и нескольких следующих заметках мы рассмотрим математические модели случайных событий. Математическая модель — это математическое выражение, представляющее случайную величину. Для дискретных случайных величин это математическое выражение известно под названием функция распределения. [1]
Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения. В этом случае можно вычислить и перечислить все значения функции распределения. В деловых, социологических и медицинских приложениях встречаются разнообразные распределения случайных величин. Одним из наиболее полезных распределений является биномиальное.
Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями.
Скачать заметку в формате Word или pdf, примеры в формате Excel2207
Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из n наблюдений. Рассмотрим в качестве примера оформление заказов. Чтобы сделать заказ клиенты компании Saxon Company могут воспользоваться интерактивной электронной формой и послать ее в компанию. Затем информационная система проверяет, нет ли в заказах ошибок, а также неполной или недостоверной информации. Любой заказ, вызывающий сомнения, помечается и включается в ежедневный отчет об исключительных ситуациях. Данные, собранные компанией, свидетельствуют, что вероятность ошибок в заказах равна 0,1. Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочных заказов в заданной выборке. Например, предположим, что клиенты заполнили четыре электронных формы. Какова вероятность, что все заказы окажутся безошибочными? Как вычислить эту вероятность? Под успехом будем понимать ошибку при заполнении формы, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочных заказов в заданной выборке.
Какие исходы мы можем наблюдать? Если выборка состоит из четырех заказов, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое-либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки n или быть отрицательным. Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n.
Допустим, что в выборке из четырех заказов наблюдаются следующие исходы:
Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0,10, вероятности указанных выше исходов вычисляются следующим образом:
Поскольку исходы не зависят друг от друга, вероятность указанной последовательности исходов равна: р*р*(1–р)*р = 0,1*0,1*0,9*0,1 = 0,0009. Если же необходимо вычислить количество вариантов выбора X объектов из выборки, содержащей n элементов, следует воспользоваться формулой сочетаний (1):
где n! = n * (n –1) * (n – 2) * … * 2 * 1 — факториал числа n, причем 0! = 1 и 1! = 1 по определению.
Это выражение часто обозначают как 
Следовательно, вероятность обнаружить три ошибочных заказа вычисляется следующим образом:
(Количество возможных последовательностей) *
(вероятность конкретной последовательности) = 4 * 0,0009 = 0,0036
Аналогично можно вычислить вероятность того, что среди четырех заказов окажутся один или два ошибочных, а также вероятность того, что все заказы ошибочны или все верны. Однако при увеличении объема выборки n определить вероятность конкретной последовательности исходов становится труднее. В этом случае следует применить соответствующую математическую модель, описывающую биномиальное распределение количества вариантов выбора X объектов из выборки, содержащей n элементов.
где Р(Х) — вероятность X успехов при заданных объеме выборки n и вероятности успеха р, X = 0, 1, … n.
Обратите внимание на то, что формула (2) представляет собой формализацию интуитивных выводов. Случайная величина X, подчиняющаяся биномиальному распределению, может принимать любое целое значение в диапазоне от 0 до n. Произведение р X (1 – р) n – X представляет собой вероятность конкретной последовательности, состоящей из X успехов в выборке, объем которой равен n. Величина 
Р(Х) = (количество возможных последовательностей) * (вероятность конкретной последовательности) =
Рассмотрим примеры, иллюстрирующие применение формулы (2).
1. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм три окажутся ошибочными? Используя формулу (2), получаем, что вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, равна
2. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными? Как показано в предыдущем примере, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0,0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными. Вероятность второго события равна
Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна
Р(Х > 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037
3. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными? Вероятность этого события
Р(X 3. Тогда Р(Х 3) = 1 – 0,0037 = 0,9963.
По мере увеличения объема выборки n вычисления, аналогичные проведенным в примере 3, становятся затруднительными. Чтобы избегать этих сложностей, многие биномиальные вероятности табулируют заранее. Некоторые из этих вероятностей приведены рис. 1. Например, чтобы получить вероятность, что Х = 2 при n = 4 и p = 0,1, следует извлечь из таблицы число, стоящее на пересечении строки Х = 2 и столбца р = 0,1.
Рис. 1. Биномиальная вероятность при n = 4, Х = 2 и р = 0,1
Биномиальное распределение можно вычислить с помощью функции Excel =БИНОМ.РАСП() (рис. 2), имеющей 4 параметра: число успехов – Х, число испытаний (или объем выборки) – n, вероятность успеха – р, параметр интегральная, принимающий значения ИСТИНА (в этом случае вычисляется вероятность не менее Х событий) или ЛОЖЬ (в этом случае вычисляется вероятность точно Х событий).
Рис. 2. Параметры функции =БИНОМ.РАСП()
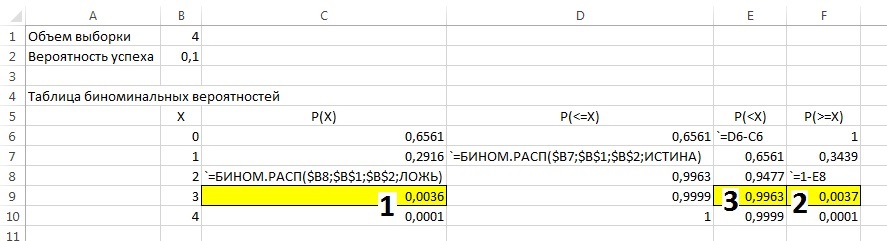
Для вышеприведенных трех примеров расчеты приведены на рис. 3 (см. также Excel-файл). В каждом столбце приведено по одной формуле. Цифрами показаны ответы на примеры соответствующего номера).
Рис. 3. Расчет биноминального распределения в Excel для n = 4 и p = 0,1
Свойства биномиального распределения
Биномиальное распределение зависит от параметров n и р. Биномиальное распределение может быть, как симметричным, так и асимметричным. Если р = 0,5, биномиальное распределение является симметричным независимо от величины параметра n. Однако, если р ≠ 0,5, распределение становится асимметричным. Чем ближе значение параметра р к 0,5 и чем больше объем выборки n, тем слабее выражена асимметрия распределения. Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку p = 0,1 (рис. 4).
Рис. 4. Гистограмма биномиального распределения при n = 4 и p = 0,1
Математическое ожидание биномиального распределения равно произведению объема выборки n на вероятность успеха р:
В среднем, при достаточно долгой серии испытаний в выборке, состоящей из четырех заказов, может оказаться р = Е(Х) = 4 х 0,1 = 0,4 неправильно заполненных форм.
Стандартное отклонение биномиального распределения
Например, стандартное отклонение количества неверно заполненных форм в бухгалтерской информационной системе равно:
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 307–313