Что такое бином в математике
БИНОМ
Полезное
Смотреть что такое «БИНОМ» в других словарях:
бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка
Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия
бином — двучлен Словарь русских синонимов. бином сущ. • двучлен Словарь русских синонимов. Контекст 5.0 Информатик. 2012. бином … Словарь синонимов
БИНОМ — (от би. и лат. nomen имя) то же, что двучлен. О биноме вида (x+y)n см. в ст. Ньютона бином … Большой Энциклопедический словарь
бином — БИНОМ, а, м. (или бином ньютона). Ирон. О чем л. кажущемся сложным, запутанным. Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита» … Словарь русского арго
Бином ПМ-2 — (ТУ5730 001 96360128 2007) – соответствует требованиям для пластифицирующих водоредуцирующих и противоморозных добавок. Обеспечивает протекание процессов гидратации цемента при температуре твердения бетона не ниже минус 18°С. Не… … Энциклопедия терминов, определений и пояснений строительных материалов
БИНОМ — сумма или разность двух одночленов. Бином Ньютона формула, выражающая произвольную натуральную степень Б. в виде многочлена, расположенного по степеням одного из членов Б … Большая политехническая энциклопедия
БИНОМ — (от би. и латинского nomen имя) (двучлен), алгебраическая сумма двух одночленов … Современная энциклопедия
БИНОМ — БИНОМ, а, муж. В математике: двучлен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
БИНОМ — муж. биномия жен. в буквосчислении: численное выражение, состоящее из двух членов; двучлен, двучленная величина. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
Бином Ньютона в школьном курсе математики
ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ
ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»
Заслуженный Учитель Математики
« Бином Ньютона. Свойства биноминальных коэффициентов»
— обучающие : познакомить с формулой бинома Ньютона, научить применять формулу бинома Ньютона при возведении в степень двучлена;
— развивающие : способствовать развитию памяти, алгоритмического и логического мышления, внимания;
— воспитательные: продолжить воспитание чувства ответственности, самостоятельности, добросовестности.)
Оборудование : компьютер, мультимедийный проектор, экран, презентация, карточки с теоретическим материалом.
Тип урока – к омбинированный;
Формы работы учащихся – фронтальная, индивидуальная.
Сообщение темы, целей урока, практической значимости рассматриваемой темы.
2. Актуализация знаний
I. Фронтальный опрос:
1) Что изучает комбинаторика?
2) Какие виды соединений или выборок вам известны?
3) Отгадать кроссворд «Комбинаторика»
5!=….(120), А 5 2 =…(20)., С 4 2 =….(8)
Сколькими способами можно разместить 5 человек на скамейке?
3. Изложение нового материала: Работа с карточками теоретического материала. Заслушивание и анализ сообщений студентов. Написание конспекта.
I) История комбинаторики
На прошлом уроке мы познакомились с основами комбинаторики. Домашнее задание для первой творческой группы было подготовить сообщение об истории возникновения комбинаторики как науки.
Какие же ученые внесли вклад в развитие комбинаторики как науки?
Одним из выдающихся умов того времени был английский ученый Исаак Ньютон. Ваше домашнее задание было подготовить сообщение об этом великом гении.
II) Исаак Ньютон- великий математик
Именно этому открытию мы посвятим наш сегодняшний урок. Запишем тему урока. Цели нашего урока : познакомиться с формулой бинома Ньютона, научиться применять формулу бинома Ньютона при возведении в степень двучлена.
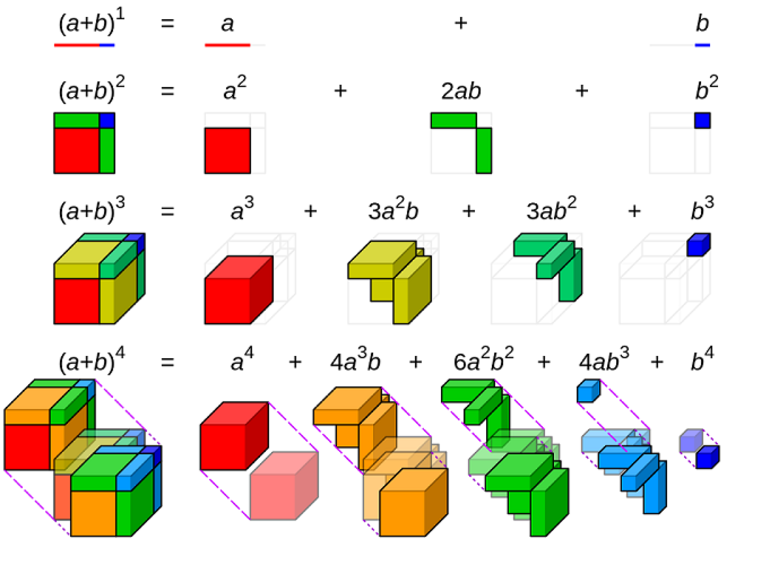
Слово бином означает «Два числа» В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.
Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах
Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?
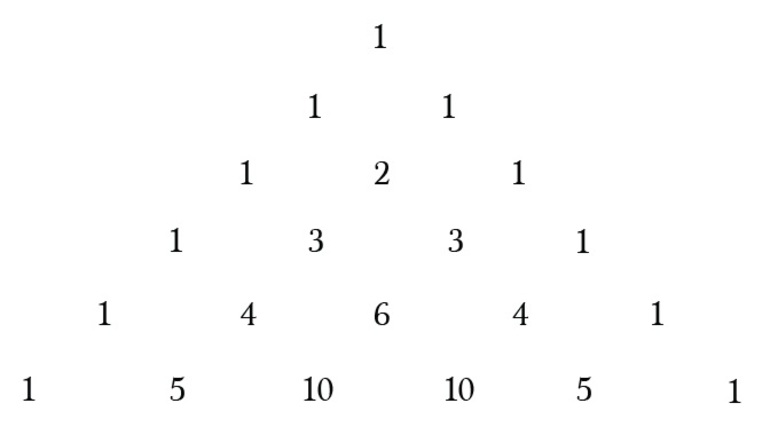
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
Возможно, вы уже догадались, что «рояль в кустах» – это треугольник Паскаля на предыдущей странице. Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1 ):
Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона :
Таким образом можно записать формулу для возведения двучлена в любую степень. Давайте заметим некоторые свойства у слагаемых в разложении двучлена по формуле Бинома Ньютона.
V) Свойства бинома Ньютона
Число слагаемых на 1 больше степени бинома.
Если в скобке знак минус, то знаки + и – чередуются.
Сумма степеней каждого слагаемого равна степени бинома.
VI) Закрепление нового материала.
Мы знакомились с вами с применением бинома Ньютона при изучении формул сокращенного умножения: Где же ещё применяется Бином Ньютона?
VII) Применение Бинома Ньютона.
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:
Полученное произведение доказывает делимость исходного выражения на 16. Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница
VIII) Что означает фразеологизм «Бином Ньютона»?
IX) Итоги урока. Рефлексия
Подумаешь, Бином Ньютона
«Подумаешь, Бином Ньютона»
Кот промяукал Бегемот
(Он Воланда слуга покорный),
Предсказывая жизни ход.
Все это только подтверждает
Ньютона гений, но давно
Бином известен был в Китае,
Арабы знали про него.
Но обобщил Ньютон решение,
Возвёл он в степень многочлен.
Избавил нас от всех сомнений
Других же нет у нас проблем.
Скажите нам совсем без прений
Зачем нам нужен тот бином?
Комбинаторику явлений
Мы без бинома не найдём.
Nov. 7, 2015
— Что нового вы узнали на уроке? Важна ли эта формула для математики? Трудно ли вам было усваивать новый материал?
Домашнее задание. Подготовка к контрольной работе.
1. Из 12 членов команды нужно выбрать капитана и заместителя. Сколькими способами можно это сделать?
Выпускники экономического института работают в трех различных организациях: 17 человек в банке,23- в фирме и 19-в налоговой инспекции. Найдите вероятность того, что случайно встреченный выпускник работает в банке?
Имеется 8 различных книг 2 из которых сборники стихов. Сколькими способами можно расставить эти книги на полке так, чтобы справочники оказались рядом?
Для игры в КВН нужно выбрать команду из 6 человек, Сколькими способами можно это сделать, если в команде должно быть мальчиков и девочек поровну, и в классе 12 девочек и 10 мальчиков?
Разложите на множители: (a-b) 9 и (3x+y) 10
Древние знания
Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.
Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.
Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.
Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.
Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:
К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.
Утверждение теоремы
Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.
Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :
Теорема может быть применена к степеням любого бинома.
С точки зрения геометрии
Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.
Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:
Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.
Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.
Биномные обобщения
Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.
Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.
Короткий путь
Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.
Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).
Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.
БИНОМ
— двучлен, сумма или разность двух алгеб-раич. выражений, называемых членами Б., напр. 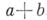


Смотреть что такое «БИНОМ» в других словарях:
БИНОМ — (от лат. bis дважды, и греч. nomos часть, отдел). Двучлен (в алгебре). Бином Ньютона общая формула для возведения двучленного количества в любую степень. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИНОМ в… … Словарь иностранных слов русского языка
бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка
Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия
бином — двучлен Словарь русских синонимов. бином сущ. • двучлен Словарь русских синонимов. Контекст 5.0 Информатик. 2012. бином … Словарь синонимов
БИНОМ — (от би. и лат. nomen имя) то же, что двучлен. О биноме вида (x+y)n см. в ст. Ньютона бином … Большой Энциклопедический словарь
бином — БИНОМ, а, м. (или бином ньютона). Ирон. О чем л. кажущемся сложным, запутанным. Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита» … Словарь русского арго
Бином ПМ-2 — (ТУ5730 001 96360128 2007) – соответствует требованиям для пластифицирующих водоредуцирующих и противоморозных добавок. Обеспечивает протекание процессов гидратации цемента при температуре твердения бетона не ниже минус 18°С. Не… … Энциклопедия терминов, определений и пояснений строительных материалов
БИНОМ — сумма или разность двух одночленов. Бином Ньютона формула, выражающая произвольную натуральную степень Б. в виде многочлена, расположенного по степеням одного из членов Б … Большая политехническая энциклопедия
БИНОМ — (от би. и латинского nomen имя) (двучлен), алгебраическая сумма двух одночленов … Современная энциклопедия
БИНОМ — БИНОМ, а, муж. В математике: двучлен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
БИНОМ — муж. биномия жен. в буквосчислении: численное выражение, состоящее из двух членов; двучлен, двучленная величина. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
Что такое Бином? Это… Значение на
Бином Ньютона — формула
С натуральным n формула Бинома Ньютона принимает вид a+bn=Cn·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn, где имеем, что Cnk=(n)!(k)!·(n-k)!=n(n-1)·(n-2)·…·(n-(k-1))(k)!- биномиальные коэффициенты, где есть n по k, k=,1,2,…,n, а «!» является знаком факториала.
В формуле сокращенного умножения a + b 2 = C 2 · a 2 + C 2 1 · a 1 · b + C 2 2 · b 2 = a 2 + 2 a b + b 2 просматривается формула бинома Ньютона, так как при n = 2 является его частным случаем.
Видео
Проверка в действии
Начать лучше с решения простой задачи, которую учитель покажет классу на уроке алгебры. Например, нужно расширить (2x-3) ³. Это было бы не слишком трудно сделать, воспользовавшись онлайн-калькулятором. Но нужно использовать бином, когда придётся столкнуться с более крупными расширениями, такими как двучлены, возведённые в 4, 5, 6, … степени.
Для начала нужно определить два члена из бинома (положения x и y формулы) и степени (буква n), до которой нужно расширить бином. Например, чтобы расширить (2x-3) ³, два члена составляют 2x и -3, а значение мощности (или n) равно 3. Следует отметить, что всякий раз, когда в биноме есть знак вычитания, очень важно помнить, что минус следует использовать только в качестве отрицательного символа в сопутствующем термине.
Замечательная вещь в теореме о биноме — это то, что она позволяет найти расширенный многочлен без умножения множества биномов вместе. Довольно интересное свойство. Оказывается, что число слагаемых в искомом расширенном полиноме всегда будет на единицу больше, чем сила, которую расширяют. Это означает, что необходимо создавать многочлен с четырьмя членами, так как мощность в этом примере равна 3.
Каждый член будет иметь (2x) и (-3), а также формулу «n выбирает k», где n = 3. Нужно записать это 4 раза, по одному на каждый член, оставив значение k в «n выбирает k». На этом этапе подсчёта значения степеней не заполняются.
Далее нужно заполнить k-значения и полномочия. Здесь можно следовать формуле суммирования, увеличивая мощность для каждого члена. Но довольно просто следовать шаблонам. Значения k в «n выбирает k» начинаются с k = 0 и увеличиваются на 1 в каждом члене. Последний член должен заканчиваться на n, равный k, в этом случае n = 3 и k = 3. Затем нужно добавить полномочия на (2x) и (-3).
Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.
С точки зрения геометрии
Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.
Биномиальные коэффициенты появляются в разложении бинома Ньютона. Обычно их записывают как ( n k) и интерпретируют, как количество способов выбора k элементов из n строки треугольника Паскаля. Коэффициент x n — k y k находят по формуле: ( n k) = n! / k! (n-k)!, которая определяется в терминах факториальной функции n!.
Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:
Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.
Или, например, общий случай. Расширение (x + y) n дает сумму 2 n произведений вида e1 e2 … en, где каждый ei равен x или y. Коэффициенты перестановки показывают, что каждый продукт равен x n — k y k для некоторого k между 0 и n. Для заданного k следующие значения равны по порядку:
Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.
Бином Ньютона — применение при решении примеров и задач
Для полного понятия использования формулы рассмотрим примеры.
Разложить выражение (a+b)5, используя формулу бинома Ньютона. Решение По треугольнику Паскаля с пятой степенью видно, что биноминальные коэффициенты – это 1, 5, 10, 10, 5, 1. То есть, получаем, что a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 является искомым разложением. Ответ: a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
Найти коэффициенты бинома Ньютона для шестого члена разложения выражения вида a+b10. Решение По условию имеем, что n=10, k=6-1=5. Тогда можно перейти к вычислению биномиального коэффициента: Cnk=C105=(10)!(5)!·10-5!=(10)!(5)!·(5)!==10·9·8·7·6(5)!=10·9·8·7·61·2·3·4·5=252 Ответ: Cnk=C105=252
Ниже приведен пример, где используется бином для доказательства делимости выражения с заданным числом.
Доказать, что значение выражения 5n+28·n-1, при n, являющимся натуральным числом, делится на 16 без остатка. Решение Необходимо представить выражение в виде 5n=4+1n и воспользоваться биномом Ньютона. Тогда получим, что 5n+28·n-1=4+1n+28·n-1==Cn·4n+Cn1·4n-1·1+…+Cnn-2·42·1n-2+Cnn-1·4·1n-1+Cnn·1n+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+n·4+1+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+32·n==16·(4n-2+Cn1·4n-3+…+Cnn-2+2·n) Ответ: Исходя из полученного выражения, видно, что исходное выражение делится на 16.
Всё ещё сложно? Наши эксперты помогут разобраться Все услуги