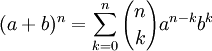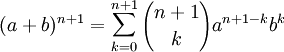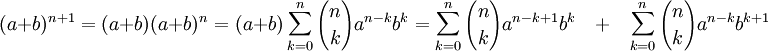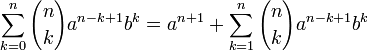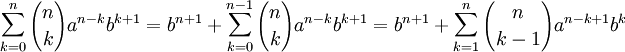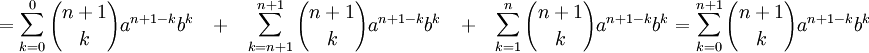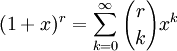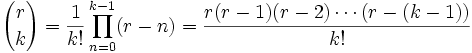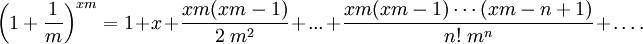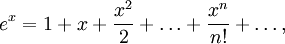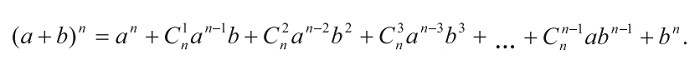Что такое бином ньютона простыми словами
Бином ньютона
Бином Ньютона — это формула
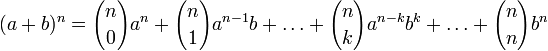
где 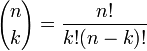
Содержание
Доказательство
Докажем это равенство, используя метод математической индукции:
Пусть утверждение для n верно:
Тогда надо доказать утверждение для n + 1 :
Извлечём из первой суммы слагаемое при k = 0
Извлечём из второй суммы слагаемое при k = n
Теперь сложим преобразованные суммы:
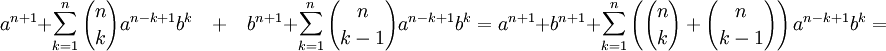
Что и требовалось доказать
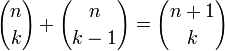
Для ненатуральных степеней
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты находятся по формуле:
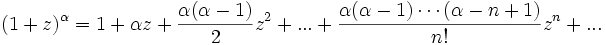
сходится при 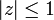
В частности, при 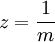
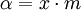
Переходя к пределу при 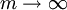
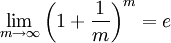
именно таким образом впервые полученное Эйлером.
История
Считается, что эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Тем не менее, она была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке. Возможно, её открыл персидский учёный, поэт и философ Омар Хайям.
Исаак Ньютон обобщил формулу для прочих показателей степени.
В художественной литературе
В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.
Об этой специфической роли бинома Ньютона в культуре писал известный математик В. А. Успенский [1].
См. также
Полезное
Смотреть что такое «Бином ньютона» в других словарях:
бином ньютона — БИНОМ, а, м. (или бином ньютона). Ирон. О чем л. кажущемся сложным, запутанным. Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита» … Словарь русского арго
БИНОМ НЬЮТОНА — БИНОМ НЬЮТОНА, математическое правило разложения алгебраического выражения (а+b)n в ряд степеней численных значений х и у (где n положительное число). При n 2 разложение выглядит таким образом: (х+у)2=х2+2ху+у2 … Научно-технический энциклопедический словарь
Бином Ньютона — алгебраическая формула, открытая Ньютоном, выражающая какую угодно степень двучлена, а именно: (х + а)n = хn + n/1(axn 1) + [n/(n 1)/1.2](а2хn 2) + …[n(n 1)(n 2)…(n m+1)/1.2.3…m](anxn m) + … или, в компактной форме, пользуясь символом n! =… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Бином Ньютона — Разг. Шутл. О чём л. сложном, запутанном. Елистратов, 41 … Большой словарь русских поговорок
Подумаешь, бином Ньютона! — Из романа (гл. 18 «Неудачливые визитеры») «Мастер и Маргарита» (1940) Михаила Афанасьевича Булгакова (1891 1940). Слова Коровьева Фагота, комментирующего диалог между Воландом и буфетчиком Андреем Фокичем Соковым. Последний пришел жаловаться на… … Словарь крылатых слов и выражений
бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка
БИНОМ — (от лат. bis дважды, и греч. nomos часть, отдел). Двучлен (в алгебре). Бином Ньютона общая формула для возведения двучленного количества в любую степень. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИНОМ в… … Словарь иностранных слов русского языка
Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия
Бином Ньютона — формула, доказательство и примеры решения
Древние знания
Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.
Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.
К VI веку н. э. индийские математики, вероятно, знали способ выразить общее правило, как частное, и выражали это примерно в таком виде: n! / (n — k)!k!. Чёткое его изложение можно найти в тексте XII века, автор которого — Бхаскар. Насколько известно, первая формулировка биноминальной теоремы и соответствующая таблица коэффициентов найдена в работе Аль-Караджи, которая цитируется Аль-Самавалем в его трудах.
Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.
Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.
В 1544 году Майкл Стифель ввёл термин «биномиальный коэффициент» и показал, как его использовать для выражения (1 + a) n с точки зрения (1 + a) n — 1 через «треугольник Паскаля». Блез Паскаль всесторонне изучил треугольник в трактате «Traité du triangle arithmétique» (1653).
Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:
К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.
Утверждение теоремы
Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.
Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :
Теорема может быть применена к степеням любого бинома.
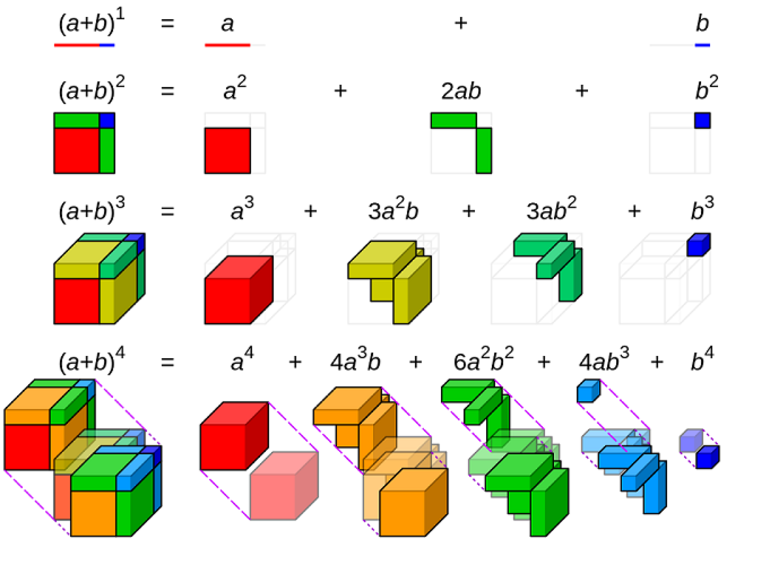
С точки зрения геометрии
Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.
Биномиальные коэффициенты появляются в разложении бинома Ньютона. Обычно их записывают как ( n k) и интерпретируют, как количество способов выбора k элементов из n строки треугольника Паскаля. Коэффициент x n — k y k находят по формуле: ( n k) = n! / k! (n-k)!, которая определяется в терминах факториальной функции n!.
Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:
Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.
Или, например, общий случай. Расширение (x + y) n дает сумму 2 n произведений вида e1 e2 … en, где каждый ei равен x или y. Коэффициенты перестановки показывают, что каждый продукт равен x n — k y k для некоторого k между 0 и n. Для заданного k следующие значения равны по порядку:
Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.
Биномные обобщения
Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.
Однако для произвольного числа r можно вычислить ( r k) = r(r — 1) ··· (r — k + 1) / k! = (r)k / k!, где (·) k является символом Похгаммера, который здесь означает падающий факториал. Это согласуется с обычными определениями. Когда r — неотрицательное целое число, биномиальные коэффициенты при k > r равны нулю, поэтому это уравнение сводится к обычной биномиальной теореме, где существует не более r + 1 ненулевых членов. Для других значений r ряд обычно имеет бесконечно много ненулевых членов.
Обобщения можно распространить на случай, когда x и y — комплексные числа. Для этой версии следует снова принять | х | > | у | и определить степени x + y и x, используя голоморфную ветвь логарифма, определённую на открытом диске радиуса | х | с центром в х. Обобщённая теорема бинома справедлива и для элементов х и у в банаховой алгебре, пока х = ух, х является обратимым, а || у / х || Проверка в действии
Начать лучше с решения простой задачи, которую учитель покажет классу на уроке алгебры. Например, нужно расширить (2x-3) ³. Это было бы не слишком трудно сделать, воспользовавшись онлайн-калькулятором. Но нужно использовать бином, когда придётся столкнуться с более крупными расширениями, такими как двучлены, возведённые в 4, 5, 6, … степени.
Для начала нужно определить два члена из бинома (положения x и y формулы) и степени (буква n), до которой нужно расширить бином. Например, чтобы расширить (2x-3) ³, два члена составляют 2x и -3, а значение мощности (или n) равно 3. Следует отметить, что всякий раз, когда в биноме есть знак вычитания, очень важно помнить, что минус следует использовать только в качестве отрицательного символа в сопутствующем термине.
Замечательная вещь в теореме о биноме — это то, что она позволяет найти расширенный многочлен без умножения множества биномов вместе. Довольно интересное свойство. Оказывается, что число слагаемых в искомом расширенном полиноме всегда будет на единицу больше, чем сила, которую расширяют. Это означает, что необходимо создавать многочлен с четырьмя членами, так как мощность в этом примере равна 3.
Каждый член будет иметь (2x) и (-3), а также формулу «n выбирает k», где n = 3. Нужно записать это 4 раза, по одному на каждый член, оставив значение k в «n выбирает k». На этом этапе подсчёта значения степеней не заполняются.
Далее нужно заполнить k-значения и полномочия. Здесь можно следовать формуле суммирования, увеличивая мощность для каждого члена. Но довольно просто следовать шаблонам. Значения k в «n выбирает k» начинаются с k = 0 и увеличиваются на 1 в каждом члене. Последний член должен заканчиваться на n, равный k, в этом случае n = 3 и k = 3. Затем нужно добавить полномочия на (2x) и (-3).
Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.
Короткий путь
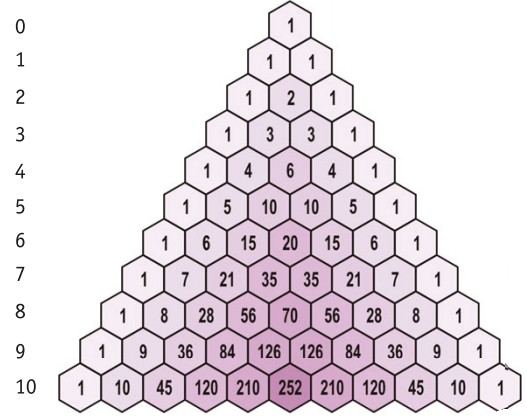
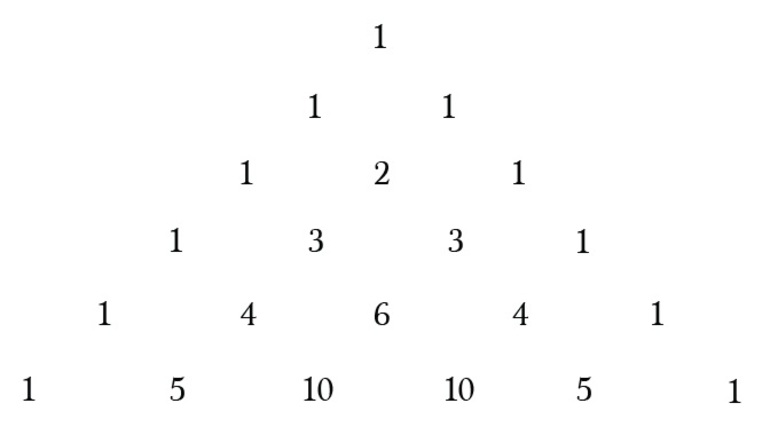
Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.
Теперь хорошая часть. В Треугольнике Паскаля спрятаны все ответы — это настоящая шпаргалка. Диаграмма ниже показывает, где находятся скрытые «n выбирает k».
Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).
Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.
Бином Ньютона
В художественной литературе бином Ньютона часто упоминается, когда речь идет о чем-либо сложном. Автор этой формулы — великий физик и математик Исаак Ньютон. Дело не только в том, что формула кажется сложной. Изучение ее то включали в программу средней школы, то выводили за рамки основного курса, но в серьезных вузах экзаменаторы спрашивали и продолжают спрашивать о биноме Ньютона.
Бином Ньютона — формула разложения произвольной натуральной степени двучлена в многочлен. Каждый из нас знает наизусть формулы квадрата суммы, но при увеличении показателя степени возникают трудности с определением коэффициентов при членах многочлена. Чтобы не совершить ошибку, можно применять формулу бинома Ньютона:
Левое число — степень n, справа — значения соответствующих биномиальных коэффициентов.
Все очень просто и запоминается на всю жизнь. Кстати, самостоятельно вспомнить и вывести формулу бинома Ньютона, нарисовав треугольник Паскаля, тоже намного проще.
Ряд историков науки приписывают Паскалю авторство не только треугольника, позволяющего находить биномиальные коэффициенты, но и самой формулы бинома. Они считают, что Паскаль вывел ее несколько раньше Ньютона, а тот лишь обобщил формулу для разных показателей степеней.
Бином Ньютона
Вы будете перенаправлены на Автор24
Бином Ньютона — это формула, использующаяся для разложения суммы двух чисел или переменных, возведённых в степень. Формула бинома Ньютона выглядит следующим образом:
$C_n^k=(a + x)^n = a^n + C^1_n \cdot a^
Биномиальные коэффициенты при этом определяются по следующей формуле:
Вывод формулы бинома Ньютона и доказательство
Все мы помним наизусть формулы разложения квадрата суммы и куба, для тех, кто всё же имеет какие-то сомнения, ниже мы привели их:
Эти формулы есть не что иное, как частные случаи второй и третьей степени для бинома Ньютона.
$(a + x)^n = A_0 + A_1x + A_2x^2 + A_3x^3 + … +A_nx^n \left(1\right)$
$((a + x)^n)’ = n(a + x)^
$(A_0 + A_1x + A_2x^2 + A_3x^3 + … +A_nx^n)’ = A_1 + 2A_2x + 3A_3x^2 + … +nA_n \cdot x^
$n \cdot (a+ x)^
Готовые работы на аналогичную тему
$n(n-1)a^
$n(n-1)\cdot … \cdot (n-k + 1)a^
Полученное выражение используется для вычисления биномиальных коэффициентов.
Сосчитаем биномиальные коэффициенты:
Теперь воспользуемся вычисленными коэффициентами для разложения бинома Ньютона:
Бином Ньютона: треугольник Паскаля
Как вы уже заметили, биномиальные коэффициенты имеют свойство повторяться, поэтому все их можно записать в виде специальной таблицы, называемой треугольником Паскаля:
Рисунок 1. Бином Ньютона: треугольник Паскаля. Автор24 — интернет-биржа студенческих работ
По рисунку 1 видно, что каждый коэффициент равен сумме двух стоящих слева и справа над ним в предыдущей строчке, так что этой таблицей можно пользоваться для более быстрого вычисления биномиальных коэффициентов в случае показателей степеней, представленных целыми неотрицательными числами.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 12 02 2021
Древние знания
Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.
Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.
Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.
Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.
Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:
К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.
Утверждение теоремы
Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.
Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :
Теорема может быть применена к степеням любого бинома.
С точки зрения геометрии
Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.
Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:
Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.
Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.
Биномные обобщения
Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.
Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.
Короткий путь
Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.
Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).
Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.