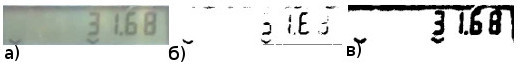Что такое биннинг пикселей
Бинаризация изображений: алгоритм Брэдли
Этот пост я хочу посвятить приятному трофею, добытому в англоязычном интернете. Речь пойдет об одном из методов адаптивной бинаризации изображений, методе Брэдли (или Брэдли-Рота, поскольку авторов двое).
Немного теории
Процесс бинаризации – это перевод цветного (или в градациях серого) изображения в двухцветное черно-белое. Главным параметром такого преобразования является порог t – значение, с которым сравнивается яркость каждого пикселя. По результатам сравнения, пикселю присваивается значение 0 или 1. Существуют различные методы бинаризации, которые можно условно разделить на две группы – глобальные и локальные. В первом случае величина порога остается неизменной в течение всего процесса бинаризации. Во втором изображение разбивается на области, в каждой из которых вычисляется локальный порог.
Главная цель бинаризации, это радикальное уменьшение количества информации, с которой приходится работать. Просто говоря, удачная бинаризация сильно упрощает последующую работу с изображением. С другой стороны, неудачи в процессе бинаризации могут привети к искажениям, таким, как разрывы в линиях, потеря значащих деталей, нарушение целостности объектов, появление шума и непредсказуемое искажение символов из-за неоднородностей фона. Различные методы бинаризации имеют свои слабые места: так, например, метод Оцу может приводить к утрате мелких деталей и „слипанию“ близлежащих символов, а метод Ниблэка грешит появлением ложных объектов в случае неоднородностей фона с низкой контрастностью. Отсюда следует, что каждый метод должен быть применен в своей области.
Объект тестирования
На данный момент я занимаюсь распознаванием показаний бытовых приборов в рамках популярной идеи „умного дома“. Вот пример изображения, с которыми работает наша группа:
Фотография была сделана темной-темной ночью в темной-темной комнате; светодиодная подсветка сбоку создает сильно неоднородный фон, а между камерой и табло прибора находится силикатное стекло, которое порождает дополнительный шум и ложные образования в области фона. Наша задача – подготовка изображения к распознаванию текста.
Здесь логично использовать локальные методы, они же адаптивные. Наиболее быстрым из классических локальных алгоритмов считается метод Ниблэка, но он плохо работает с низкоконтрастными неровностями фона, которые в нашем случае заполняют изображение чуть меньше, чем полностью. Чтобы исправить этот недостаток, умные люди разработали несколько модификаций метода Ниблэка, называемых „ниблэковскими“. В моем случае один из них, метод Кристиана, показывал хорошие результаты на большинстве образцов, и чуть не был принят в качестве рабочего варианта. Однако на других образцах после применения этого алгоритма появлялись искажения.
а) метод Ниблэка б) метод Кристиана
Суть метода Брэдли
Само по себе сравнение двух величин – порога и яркости пикселя, — является элементарной задачей. Не в этом соль. Трудность заключается в нахождении порогового значения, которое должно максимально надежно отделять символы не только от фона, но и от шума, теней, бликов и прочего информационного мусора. Часто для этого прибегают к методам математической статистики. В методе Брэдли мы заходим с другой стороны – со стороны интегральных изображений.
Интегральные изображения
Интегральные изображения – это не только эффективный и быстрый (всего за один проход по изображению) способ найти сумму значений пикселей, но и простой способ найти среднее значение яркости в пределах заданного участка изображения.
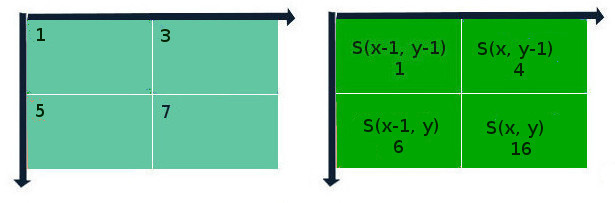
Как это работает? Да элементарно. Допустим, у нас есть 8-битное изображение в оттенках серого (цветное изображение можно перевести в оттенки серого, пользуясь формулой I = 0.2125R + 0.7154G + 0.0721B). В таком случае, значение элемента интегрального изображения рассчитывается по формуле:
S(x, y) = I(x, y) + S(x-1, y) + S(x, y-1) – S(x-1, y-1);
где S – результат предыдущих итераций для данной позиции пикселя, I – яркость пикселя исходного изображения. Если координаты выходят за пределы изображения, они считаются нулевыми. Сущность этого метода „на пальцах“ представлена на схеме ниже:
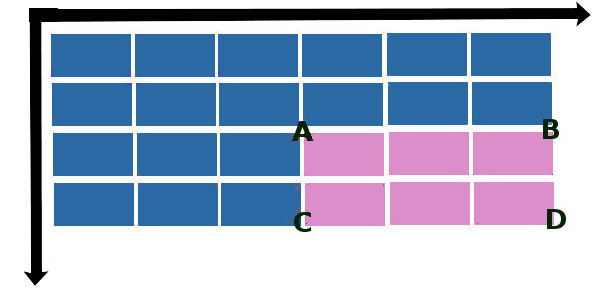
Лайфхак состоит в том, что, один раз составив интегральную матрицу изображения, можно быстро вычислять сумму значений пикселей любой прямоугольной области в пределах этого изображения. Пусть ABCD – интересующая нас прямоугольная область.
Тогда суммарная яркость S в этой области вычисляется по формуле:
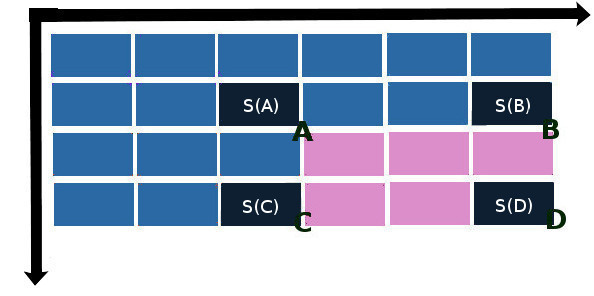
S(x, y) = S(A) + S(D) – S(B) – S©
где S(A), S(B), S© и S(D) – значения элементов интегральной матрицы в направлении на „северо-запад“ от пересечений сторон прямоугольника:
Реализация
Если вы дочитали до этого места, то вы почти разобрались в алгоритме Брэдли. Дальше все просто. Разбиваем изображение на несколько областей со стороной d, берем среднее от суммы значений пикселей Im в этой области, добавляем некоторую величину t, сравниваем значение каждого пикселя с получившимся результатом. Im+t – и есть наша искомая пороговая величина. Брэдли и Рот берут значения d и t соответственно 1/8 от ширины изображения и 15% от среднего значения яркости пикселей по области. Ну а вообще говоря, оба этих параметра могут и должны изменяться в соответствии с конкретной ситуацией. Так, если размеры объекта будут больше площади квадрата со стороной, равной d, то центр этого объекта может быть принят алгоритмом как фон, и проблема решается уменьшением значения d, однако при этом могут быть потеряны мелкие детали изображения.
И вот как это выглядит на нашем примере:
После медианной фильтрации:
Реализация алгоритма Брэдли-Рота на С++ представлена ниже:
Достоинства и недостатки
Достоинствами метода Брэдли-Рота являются простота реализации и высокая скорость выполнения; для большинства случаев нет нужды подбирать параметры. Метод хорошо работает с неоднородным фоном.
Из последнего достоинства логически вытекает недостаток метода Брэдли, а именно, плохая чувствительность к низкоконтрастным деталям изображения:
а) оригинальное изображение б) метод Брэдли в) метод Кристиана
Что такое бинаризация и как она помогает сделать ваши фото лучше
В последние годы, когда речь в какой-нибудь статье, видео или презентации заходила о возможностях камеры очередного смартфона, вы наверняка не раз слышали или видели такие термины, как пиксельный биннинг, бинаризация или технология объединения пикселей. Как вы уже поняли, все это одна технология, но что она из себя представляет и зачем вообще нужна, мы постараемся разобраться в этом материале.
А что такое пиксели?
Чтобы понять, что такое бинаризация (технология объединения пикселей), для начала нужно разобраться, что такое в этом контексте пиксели. Пиксели – физические элементы на сенсоре камеры, которые захватывают свет во время съемки.
Размер этих самых пикселей измеряется в микронах (миллионных долях метра), и размер пикселя в один микрон или меньше считается маленьким. Для примера, камеры смартфонов iPhone XS Max, Google Pixel 3 и Galaxy S10 обладают большими пикселями размером 1,4 микрона.
Я думаю, нет необходимости, объяснять, что чем больше размер пикселей, тем лучше, потому что большие пиксели могут захватываться больше света, а это в свою очередь верный признак хорошей фотографии. Особенно разница камер с большими и маленькими пикселями заметна при съемке в условиях низкой освещенности. Если вы снимаете где-то в помещении или на улице, но вечером или ночью, то для того, чтобы фотография не вышла похожей на Черный квадрат Малевича, камере нужно захватить как можно больше практически отсутствующего в этих условиях света, а если пиксели на сенсоре будут недостаточно большими, то и света много собрать не получится – как итог, фотография выйдет темная и с большим количеством шумов.
А если пиксели в камере сделать большими, то и размер модуля камеры от этого сильно увеличится. Можно не увеличивать размер модуля и увеличить размер пикселей, но тогда этих больших пикселей в небольшой модуль поместится немного, а разрешение фото при этом сильно пострадает. Для современных тонких и изящных смартфонов нужна такая же тонкая камера, и желательно, чтобы из корпуса не торчала. В таких обстоятельствах производителям приходится как-то исхитряться, чтобы усидеть на двух стульях сразу (камеру поменьше, но пиксели побольше) – здесь то и пригодилась технология под названием бинаризация.
Бинаризация – одна из важнейших технологий в современной фотографии
В общем и целом, бинаризация – это процесс объединения информации, полученной с четырех пикселей таким образом, словно она была получена одним большим пикселем. Таким образом, фотография, сделанная на камеру с пикселями размером 0,9 микрон, будет соответствовать тому, что может сделать камера с большими пикселями в 1,8 микрон.
Обратной стороной этой медали является четырехкратное уменьшение разрешения фотографий, которое происходит вследствие объединения четырех маленьких пикселей в один большой. Это значит, что мобильная камера с высоким по современным меркам разрешением сенсора 48 Мп при задействованной технологии бинаризации на выходе способна выдать снимок с разрешением лишь 12 Мп. А теперь вспомним, что у некоторых смартфонов разрешение камеры составляет всего 16 Мп, а это означает, что при объединении пикселей для более качественного снимка в темноте, мы получим фото, качество которого будет соответствовать камере со смешными 4 Мп.
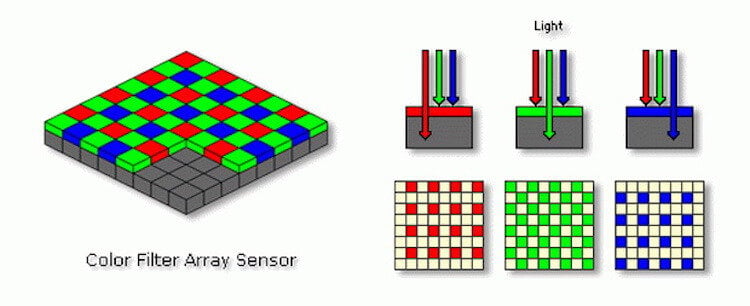
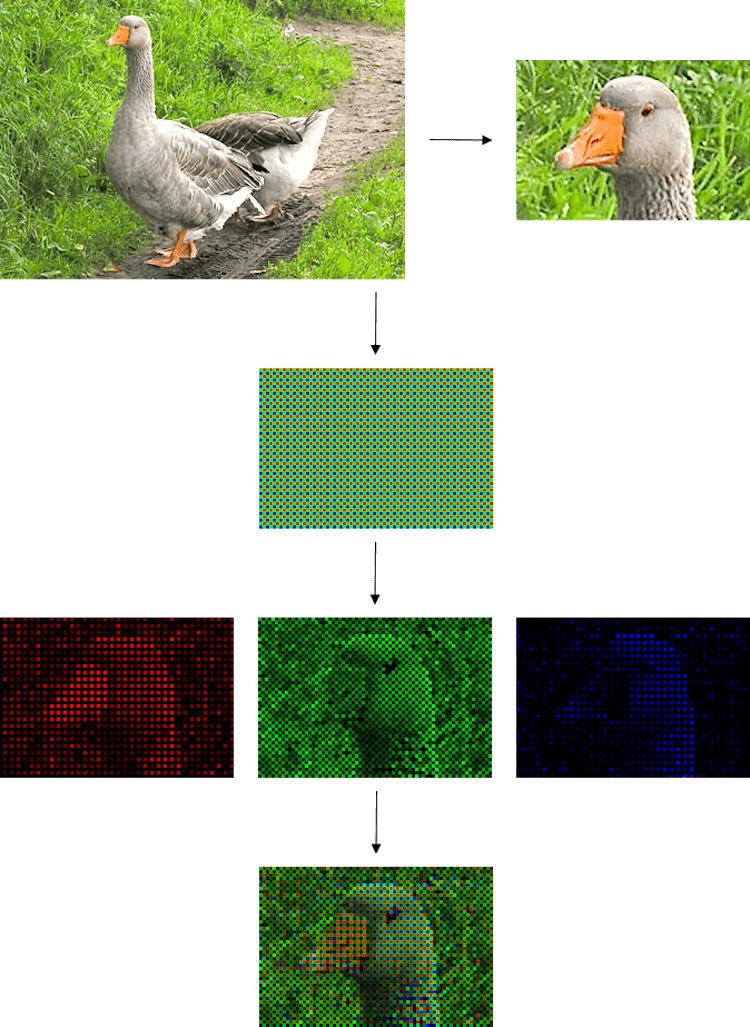
Вообще, пиксельный биннинг стал возможным благодаря использованию в сенсорах камер так называемого фильтра Байера. Фильтр Байера – это двумерный массив цветных фильтров, которыми накрыты фотодиоды всех современных фотоматриц. Этот фильтр используется для получения цветного изображения в матрицах цифровых фотоаппаратов, видеокамер и сканеров. Стандартный Фильтр Байера, который, наверняка, используется в вашем смартфоне, состоит из 25% красных элементов, 25% синих и 50% зеленых элементов. По данным ресурса Cambridge in Color, этот фильтр предназначен для имитации человеческого глаза, чувствительность которого наиболее высока именно к зеленому свету. Как только сенсор камеры захватывает картинку, она интерполируется и обрабатывается для получения окончательного, полноцветного изображения.
В сочетании с Фильтром Байера технология объединения пикселей дает нам с вами возможность делать фотографии высокого разрешения при дневном освещении и фотографии чуть меньшего разрешения, но также с меньшим количеством шумов и большим уровнем яркости в условиях недостаточной освещенности.
Кто уже сейчас использует бинаризацию?
Если у производителя есть смартфон с камерой 32 Мп, 40 Мп или 48 Мп, то можете наверняка быть уверены, что в нем используется технология объединения пикселей. Самыми известными на данный момент устройствами с этого технологией являются Xiaomi Redmi Note 7, Xiaomi Mi 9, Honor View 20, Huawei Nova 4, Vivo V15 Pro и ZTE Blade V10.
Как я упоминал выше, на рынке есть и смартфоны с камерами меньшего разрешения, но при этом использующие бинаризацию. Среди таких смартфонов LG G7 ThinQ, LG V30s ThinQ, Xiaomi Redmi S2 и Mi A2. В смартфонах LG есть режим Super Bright, который позволяет сделать на 16 Мп-сенсор яркую ночную 4 Мп-фотографию.
Очевидно, что камеры с более высоким разрешением больше подходят для вышеописанной технологии (особенно основные, а не фронтальные, камеры), так как на выходе разрешение снимком урезается аж в четыре раза. Благо, после недавних новостей от производителя мобильных процессоров Qualcomm о том, что компания внедрила в свои чипсеты поддержку камер с разрешением более 100 Мп, уже до конца этого года мы ждем появления первых смартфонов с новыми умопомрачительными камерами.
Делитесь своим мнением в комментариях под этим материалом и в нашем Telegram-чате.
Биннинг пикселей «для чайников». Работает ли эта технология на смартфонах?
Биннинг пикселей — это объединение нескольких маленьких пикселей в один крупный с целью улучшить качество изображения.
Подобная технология появилась не вчера и даже не 10 лет назад, но в мобильной фотографии биннинг стал сверхпопулярным буквально пару лет назад — в тот самым момент, когда на рынке стали появляться доступные камерофоны с 48-Мп камерами. Производители так увлеклись этой технологией, что только за один 2019 год прошли путь от 12 до 108 мегапикселей!
Сегодня практически все флагманские камерофоны используют биннинг, объединяя в группы по 4 и даже 9 пикселей. Но зачем? Есть ли в этом какой-то практический смысл или это очередной маркетинговый инструмент?
Основная проблема заключается в том, что мобильные матрицы не увеличиваются пропорционально росту их разрешения, а значит, приходится сокращать размер каждого пикселя.
В 2019 году мы начали с 800-нанометровых пикселей (0.8 мкм), размер которых вплотную подошел к длине волны красного света. А совсем недавно Samsung представила первый 200-Мп сенсор с пикселями 640 нм! То есть, размер пикселя стал де-факто меньше длины волны красного света (625 — 740 нанометров).
Но это тема для другого разговора. Сейчас же важно понять, есть ли какой-то толк от объединения четырех или девяти 0.8-мкм пикселей в один, размером 1.6 или 2.4 микрометра. Ведь именно такие конфигурации сегодня встречаются чаще всего.
Введение в курс дела. Или о чем вообще разговор?
Как вы знаете, матрица любой цифровой камеры, будь-то зеркальный фотоаппарат или смартфон, не способна различать цвета. Пиксель (кусочек кремния) умеет только улавливать количество света (яркость) безотносительно к его цвету.
Для этого мы просто над каждым пикселем размещаем цветное стеклышко, которое и будет пропускать только свой цвет. В итоге, кусок кремния под красным фильтром будет фиксировать количество только «красных» фотонов из общего потока и так далее:
Именно так устроены пиксели на матрице любой камеры, кроме современных — тех, что используют биннинг. Эти матрицы спроектированы немного по-другому.
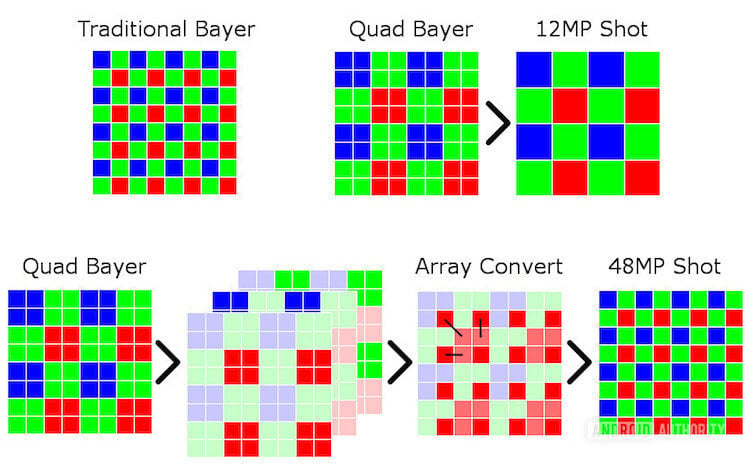
Если производитель заявляет о 48 мегапикселях, то на такой матрице действительно используется 48 миллионов физических пикселей (кусочков светочувствительного кремния). Однако все они собраны в группы по 4 пикселя, которые накрыты одним цветным фильтром:
Но зачем такие сложности? Почему бы просто не разместить 48 миллионов крохотных пикселей, каждый со своим отдельным маленьким цветным фильтром?
Сделано это для того, чтобы при необходимости 48-Мп матрица «превращалась» в 12 мегапикселей. То есть, чтобы 4 пикселя под одним цветным фильтром работали как один более крупный пиксель одного цвета.
А когда в этом нет нужды, каждый пиксель может работать отдельно, выдавая фото с более высокой детализацией:
Получается, пиксели на современных матрицах могут изменять свой размер при необходимости от 0.8 мкм до 1.6 или даже 2.4 мкм, в зависимости от типа биннинга.
Но всё это лишь красивая теория, а как обстоят дела в реальности? Может ли биннинг реально улучшить качество снимков? Действительно ли группа маленьких пикселей ведет себя так, как один большой?
Ответить на этот вопрос невозможно, если не понимать, в чем, собственно, преимущество больших пикселей перед маленькими. Мы должны чётко осознавать, каким образом сам размер пикселя влияет на качество фотографии. И только потом можно разбираться, действительно ли биннинг увеличивает размер пикселя.
Почему один большой пиксель лучше одного маленького? Или поговорим о случайностях
Давайте представим, что у нас есть идеальный профессиональный фотоаппарат. Под словом идеальный я подразумеваю, что все пиксели этой камеры без малейших искажений фиксируют каждый падающий фотон света, затем все фотоны подсчитываются и их количество оцифровывается с максимальной точностью.
Будет ли такая камера всегда выдавать снимки превосходного качества? К сожалению, нет. Качество фотографий в этом случае будет полностью зависеть от количества света, которое захватит фотоаппарат.
И проблема не в том, что при недостаточном освещении снимки будут просто темноватыми, а при хорошем — яркими. Несмотря на безупречное качество нашей идеальной камеры, при плохом освещении она будет выдавать грязные фотографии с огромным количеством шума.
Вот пример сцены, снятой на «идеальную камеру» с разным уровнем освещенности. Слева показан снимок, на каждый пиксель которого в среднем падало по 10 фотонов, а справа — 1000 фотонов:
Откуда же взялась эта «грязь» на фотографии слева? Почему при недостаточном освещении идеальная камера выдала столько шума вместо того, чтобы просто выдать более тёмную копию той фотографии, что показана справа?
Проблема заключается в самой природе света. Когда его становится слишком мало (например, мы сократили время выдержки или вокруг просто недостаточно света), фотоны начинают «играть в кости», выбрасывая каждый раз случайный результат.
Сколько бы раз мы ни пытались сделать снимок в условиях плохой освещенности, мы всегда будем получать разный результат.
К примеру, если мы сделаем 5 снимков чисто белой стены, то один и тот же пиксель каждый раз будет фиксировать разное количество фотонов. Скажем, во время первого снимка на него упадет 10 фотонов, второго — 12, третьего — 8 и так далее.
В результате, одна и та же точка одного и того же предмета на каждом снимке будет отличаться. И чем меньше было света, тем сильнее это различие. Более того, даже на одном снимке яркость всех точек одинаково белой стены будет также отличаться, ведь на соседние пиксели упадет разное количество фотонов.
Именно это мы и увидели на фото выше. Там, где пиксели неба должны были быть одного цвета, на «грязном» снимке яркость каждой конкретной точки сильно отличалась от яркости соседней.
Что такое шум и откуда он берется?
На самом деле, никакой мистики в этом нет. Падение фотонов на матрицу (или на каждый конкретный пиксель) — это такое же случайное событие, как и падение капель дождя на тротуарную плитку.
Когда идет моросящий дождик с низкой интенсивностью, на каждую плитку упадет совершенно разное количество капель. И чем реже падают капли, тем сильнее будет отличаться их общее количество на плитках.
Так и со светом. От белой стены на один пиксель может прилететь 10 фотонов, на другой — 12, а на третий — 8. Но чтобы стена на снимке выглядела такой же чисто белой, как и в жизни, на каждый пиксель должно упасть одинаковое количество фотонов.
Это естественное отклонение количества упавших фотонов от ожидаемого и называется шумом (более точно — фотонным или дробовым шумом). Чем это отклонение сильнее, тем сильнее будет отличаться и яркость соответствующей точки на снимке.
Но как же нам определить уровень шума?
Для этого достаточно выполнить простую инструкцию:
Чтобы всё стало предельно ясно, рассмотрим простой пример.
Пример
Если первый раз на пиксель упало 8 фотонов, второй — 10, а третий — 12, тогда в среднем на пиксель падало 10 фотонов, так как (8+10+12)/3 = 10.
Теперь нам нужно понять, насколько отличается количество фотонов, падающее на пиксель каждый раз, от среднего значения. Если первый раз на пиксель упало 8 фотонов, а среднее значение равняется 10, тогда мы получим 8-10=-2.
Соответственно, количество фотонов, упавших на пиксель в первый раз, отличается от среднего значения на -2, во второй раз — на 0 (так как 10 — это и есть среднее количество фотонов), а последний раз — на +2, так как 12-10=2.
Осталось сложить все эти отклонения и разделить на 3. Так мы и узнаем средний разброс значений или шум:
(-2+0+2)/3=0
Ноль!? Получается, что в среднем разброса количества фотонов и не было вовсе!? Но это же, очевидно, противоречит нашему наблюдению.
Конечно, мы допустили логическую ошибку, ведь количество фотонов отличалось как в положительную, так и отрицательную сторону. Сложив эти отклонения, мы их компенсировали, то есть, пришли к нулю.
Как же нам выйти из этой ситуации? Нужно избавиться от отрицательных чисел, для чего достаточно просто возвести их в квадрат. Пробуем:
(-2) 2 +0 2 +2 2 =4+0+4=8, теперь делим 8 на 3 и получаем 2.7.
Вот оно! Средний уровень шума составил 2.7 фотона, то есть, количество фотонов (а значит и яркость каждой точки) в среднем отличается на 2.7. Верно? И снова, нет!
Полученное нами число — это важнейший показатель в статистике, который называется дисперсией. Дисперсия показывает, как сильно разбросаны значения случайных величин или событий.
И это практически то, что нам нужно, за одним серьезным исключением — мы же возводили все значения отклонений в квадрат. То есть, дисперсия показывает среднее отклонение значений от среднего, возведенное в квадрат.
Чтобы узнать реальное отклонение значений от среднего (в статистике это называется стандартным отклонением), нужно избавиться от квадрата, для чего достаточно просто взять квадратный корень из дисперсии:
Стандартное отклонение = √2.7 = 1.64
Вот мы и получили заветную цифру! Это и есть уровень шума или то, насколько в среднем количество фотонов в конкретном пикселе отличается от ожидаемого или среднего.
Отношение сигнал/шум как важнейший показатель качества
Итак, представьте, что на конкретный пиксель нашей мобильной матрицы падает в среднем 10 фотонов. Как узнать уровень шума для этого пикселя при таком количестве фотонов? Неужели нам нужно что-то подсчитывать, суммировать, возводить в квадрат, а затем брать квадратный корень!?
К счастью, ничего этого делать не нужно. Дело в том, что дождь, подбрасывание монетки, падение фотонов или количество звонков в колл-центр — это особый вид случайных событий, который описывается так называемым законом Пуассона (или распределением Пуассона).
А если так, тогда согласно распределению Пуассона, дисперсия — это и есть среднее значение.
В нашем предыдущем примере на один пиксель в среднем падало 10 фотонов. Так как в реальной жизни (а не рассмотренном нами примере) падение фотонов распределяется по закону Пуассона, нам не нужно определять дисперсию, высчитывая все отклонения от среднего, суммируя их квадраты и пр. Число 10 — это уже и среднее значение, и дисперсия одновременно по определению.
Другими словами, если какие-то случайные события распределяются по закону Пуассона, тогда мы можем посчитать средний результат, а затем найти среднее отклонение всех его значений в квадрате и мы получим то же число. То есть, среднее значение будет равняться дисперсии. Поэтому высчитывать её отдельно не нужно.
В таком случае, чтобы узнать уровень шума (посчитать стандартное или реальное отклонение), нам нужно просто взять квадратный корень из числа 10 (из дисперсии).
Это и есть основное правило, которое описывает количество фотонного шума в пикселях.
Если на пиксель в среднем падает по 100 фотонов, уровень шума будет √100 или 10 фотонов, если падает в среднем 1000 фотонов, уровень шума будет √1000 или 31 фотон. Так как, повторюсь, среднее количество фотонов при распределении Пуассона — это и есть дисперсия (среднее отклонение всех значений в квадрате).
Отсюда мы приходим к важнейшему показателю качества изображения — отношению сигнала к шуму (SNR).
Если на один пиксель в среднем падает 10 фотонов, шум будет равняться √10 или
3 фотона. Тогда отношение сигнал/шум или SNR для такого пикселя будет составлять 10/3 = 3.33. То есть, уровень сигнала (10 фотонов) отличается от бесполезной информации или шума (3 фотона) всего в
3 раза и это очень плохо.
Увидеть такой шум на глаз — проще простого, ведь яркость пикселей, которая должна была быть идентичной (как в случае с белой стеной), на фото будет отличаться на треть (100% разделить на SNR).
Если же, скажем, количество фотонов будет 1000, а шум — 31 фотон (√1000), тогда SNR=1000/31=32, то есть, полезный сигнал отличается от бесполезного (шума) в 32 раза! Соответственно, яркость пикселей, которая должна была быть идентичной, в реальности будет отличаться всего на 3% (100%/32=3%)!
Когда света становится очень много и на каждый пиксель падает огромное количество фотонов, скажем, 50000, тогда заметить фотонный шум вообще невозможно. Ведь шум из 50 тыс. фотонов — это 223 фотона, соответственно SNR=223, а значит, яркость каждой точки будет отличаться не более, чем на 0.4% (при оцифровке сигнала такая разница, скорее всего, буде вообще проигнорирована и яркость пикселей не будет отличаться вовсе).
Когда на тротуарную плитку упало несколько капель дождя, какой-то участок плитки будет более сухим, а где-то будет больше воды. Но когда идет ливень, вся плитка будет одинаково залита водой и увидеть какое-то различие невозможно.
Почему большой пиксель лучше маленького в плане SNR?
Думаю, вы уже прекрасно понимаете, что на более крупный пиксель упадет больше фотонов, соответственно, его сигнал/шум будет выше.
Если на 4 маленьких пикселя падает по 25 фотонов, то, будь на их месте один большой пиксель, на него бы упало 100 фотонов:
Мы можем легко посчитать SNR каждого пикселя:
Получается, если площадь крупного пикселя в 4 раза больше маленького, то его SNR будет в 2 раза выше.
Поэтому при недостаточном освещении мы можем делать снимок чище за счет увеличения размеров пикселей на матрице, чтобы на каждый из них падало больше фотонов.
Работает ли на смартфонах биннинг пикселей?
Теперь мы можем ответить на главный вопрос — действительно ли «программное» объединение пикселей увеличивает их SNR или сигнал/шум.
Почему программное? Потому что физически на матрице 4 пикселя не «склеиваются» в один большой. Это всё те же 4 маленьких физических пикселя, с которых смартфон считывает небольшой сигнал и программно объединяет его, увеличивая в 4 раза.
Логика подсказывает, что это должно работать в идеальной камере. То есть, нет никакой разницы, сколько пикселей размещено на площади, скажем, 2.4×2.4 мкм. Если на этот участок сенсора падает 540 фотонов, они упадут сюда в любом случае, будь там 1 большой пиксель (2.4 мкм) или 9 маленьких (0.8 мкм).
Вы можете подумать, что 9 маленьких пикселей не занимают в реальности всей площади одного большого, ведь между пикселями есть перегородки, а внутри, помимо светочувствительного кремния, размещена и другая электроника (транзисторы, конденсаторы и пр.).
Поэтому, может показаться, что маленькие пиксели в группе менее эффективны, чем 1 большой:
Но в реальности это не так. Чтобы исключить подобную проблему, все пиксели накрываются микролинзами, которые нужным образом перенаправляют падающий мимо светочувствительного элемента (фотодиода) свет, чтобы ничего не потерялось по пути:
Поэтому, когда камера смартфона применяет биннинг, практически нет никакой разницы, находится ли на матрице один крупный пиксель или, скажем, 9 маленьких. В первом случае камера просто считывает 540 фотонов и получает фотонный шум 23 фотона (√540). Во втором случае камера считывает в среднем по 60 фотонов с 9 маленьких пикселей, шум которых равняется 8 фотонам (√60).
Затем при биннинге складывается как сигнал (60*9), так и шум √(60*9), в результате чего получаем те же сигнал 540 и шум 23 фотона, что и в случае с большим пикселем. А значит, SNR большого пикселя равен SNR группе из нескольких маленьких пикселей.
Получается, биннинг реально работает? Да, только с одним но…
У нас нет идеальной камеры!
До этого мы говорили только о гипотетической камере, которая не вносит никаких искажений в сигнал. Сколько фотонов упало, столько и оцифровали. Но в реальном мире сигнал, проходя по пути от фотона до точки на фото, искажается множество раз.
Прежде всего, электроника камеры вообще не имеет никакого дела с фотонами. Мы не собираем фотоны на матрице, не подсчитываем и не оцифровываем их.
Когда фотон падает на кусочек кремния, он может «раствориться» в нём, выбив электрон из атома кремния (фотодиода). А может и не выбить. Это первое, что следует учитывать при расчете SNR (в «идеальной камере» фотон всегда выбивал электрон).
Как нам отличить электрон, который появился из-за упавшего фотона, от электрона, который вырвался сам? Естественно, никак. Поэтому при расчете SNR нужно учитывать тепловой шум (случайное количество электронов от так называемого темнового тока 4 или тепла).
Дальше мы считываем напряжение, образованное электронами и в конце оцифровываем его. Но представьте, сколько должно стоить оборудование, способное считывать напряжение с точностью до заряда одного электрона?
Поэтому сам процесс считывания вносит искажение в сигнал и это дополнительный шум, который нужно учитывать при расчете SNR пикселя.
Если мы хотим увидеть более реалистичный прирост качества сигнала, который дает биннинг в современных матрицах, нам нужно модифицировать нашу формулу, которая выглядела так:
SNR=фотоны / √фотоны
Когда 100 фотонов попадало в идеальную камеру, мы рассчитывали SNR, делив 100 (сигнал) на √100 (шум) и получали SNR=10. Но в неидеальном мире нужно учитывать дополнительный шум:
SNR=(фотоны * квантовую_эффективность) / √(фотоны + темновой_ток * время_выдержки + шум_считывания 2 )
Не пугайтесь этой формулы, её можно упростить.
Так как речь идет о камере смартфона, можно выбросить из этого уравнения темновой_ток * время_выдержки, так как тепловой шум является проблемой в астрофотографии, где используются очень длинные выдержки (от 2 минут и больше). На смартфонах выдержка редко превышает 1 секунду, поэтому в мобильной матрице электроны не отрываются от атомов из-за температуры.
Квантовая эффективность — это процент фотонов, которые упали на пиксель и выбили электрон. Если квантовая эффективность пикселя равняется 80%, тогда нужно количество упавших фотонов умножить на 0.8. Но мы можем также выбросить эту переменную, так как она не имеет отношения к теме нашего разговора, ведь квантовая эффективность не зависит от размера пикселя.
После всех упрощений наша формула будет выглядеть так:
SNR=фотоны / √(фотоны + шум_считывания 2 )
Вот здесь-то мы и видим основное ограничение биннинга. Один крупный пиксель не равен по SNR нескольким маленьким, так как при считывании сигнала с каждого маленького пикселя мы вносим шум считывания.
Поэтому, сигнал/шум одного большого пикселя будет отличаться от SNR четырех маленьких пикселей на тот самый шум считывания, так как до объединения пикселей мы считываем сигнал с маленьких пикселей 4 раза.
Чтобы окончательно разобраться в этой разнице, давайте рассмотрим простой пример. Представьте, что на площадь 1.6*1.6 (мкм) падает 200 фотонов, при этом шум считывания пикселей равен 2 электронам. То есть, если 200 фотонов выбили 200 электронов, то электроника может считать 198 или 202 электрона.
Теперь сравним сигнал/шум в разных сценариях:
SNR большого пикселя (матрица состоит из относительно крупных пикселей 1.6 мкм)
Так как всю площадь 1.6×1.6 мкм занимает один пиксель, то все 200 фотонов падают именно на него. Нам остается считать эту информацию, внеся 1 раз шум считывания (2 электрона). Вычислим SNR этого пикселя:
SNR маленького пикселя (матрица состоит из крохотных 0.8-мкм пикселей без биннинга)
Так как на площади 1.6х1.6 мкм располагается 4 маленьких пикселя, то на каждый конкретный пиксель упадет по 50 фотонов (200/4). Чтобы узнать сигнал/шум одного маленького пикселя остается лишь считать с него информацию, внеся 1 раз шум считывания:
SNR «увеличенного» пикселя после биннинга
Если наша матрица поддерживает биннинг, тогда нам нужно суммировать все фотоны с четырех маленьких пикселей, но для этого придется 4 раза считывать информацию, внося 4 раза шум считывания. Поэтому сигнал/шум «виртуального» большого пикселя будет составлять:
Из этого примера мы видим, что качество сигнала большого пикселя в 2 раза выше качества сигнала маленького. Однако при биннинге маленьких пикселей, даже с учетом вносимого шума считывания, качество сигнала «объединенного пикселя» практически не отличается от SNR физически большого пикселя.
Конечно, это при условии, что шум считывания равняется двум электронам. Какой он в действительности — не знает никто, так как производители смартфонов не раскрывают этой информации.
Шум чтения в крупных пикселях зеркальных фотоаппаратов может варьироваться от 1.5 электрона до 5, а иногда и выше. Но стоит учитывать, что зачастую шум считывания тем меньше, чем меньше сам пиксель.
Вместо выводов
К сожалению, эта статья не дает ответов на многие вопросы. В частности, мы рассматривали биннинг пикселей только в контексте плохого освещения, когда фотонов очень мало. А что будет при хорошем освещении?
Еще более важный вопрос заключается в том, что лучше — матрица с большими пикселями или несколькими маленькими? Помогает ли биннинг увеличить динамический диапазон камеры при хорошем освещении?
Обо всём этом мы поговорим как-нибудь в другой раз, но на главный вопрос, надеюсь, эта статья дала исчерпывающий ответ.
Биннинг пикселей — это не маркетинговая уловка, а реально работающий инструмент, который снижает количество шума и в целом улучшает качество снимков, оставляя при этом возможность снимать с более высоким разрешением, когда это уместно.
Понимая, как работает биннинг, вы можете использовать еще более простое правило. Если матрица объединяет пиксели 2×2, значит, это улучшает SNR (отношение сигнала к шуму) «склеенного» пикселя в 2 раза, если речь идет о биннинге 3×3, значит SNR увеличивается в 3 раза и т.д.
Разумеется, при биннинге разрешение снимков падает пропорционально. Увеличивая SNR в 2 раза, мы сокращаем разрешение в 4 раза (2 2 ), если хотим увеличить сигнал/шум в 3 раза, разрешение упадет в 9 раз (3 2 ) и т.д.
Иногда встречаются ситуации, когда смартфон не способен выдавать снимки в полном разрешении. У нас частенько бывали такие аппараты на обзорах.
К примеру, 48-Мп камера какого-то смартфона всегда выдает только 12-Мп снимки, полученные при биннинге. Если же пользователь выбирает в настройках полное разрешение, то смартфон всё равно делает 12-Мп снимок с биннингом, а затем просто растягивает картинку в 4 раза. В этом, естественно, нет никакого смысла.
Но тогда может возникнуть другой вопрос — в чем, собственно, сложность снимать в полном разрешении? Почему некоторые смартфоны всегда выдают результат в биннинге, если они в любом случае считывают каждый отдельный пиксель и только потом «склеивают» их в группы?
Ответ заключается в цветных фильтрах. Если вы посмотрите на картинки в начале статьи, то заметите, что пиксели группируются под фильтром одного цвета. Соответственно, чтобы восстановить исходный цвет, гораздо проще «склеить» группу пикселей в один, так как они уже накрыты одним цветом.
Если же попытаться восстановить полное разрешение, то есть, цвет каждого отдельного пикселя, нужно использовать гораздо более сложный и требовательный к вычислительным ресурсам алгоритм. Тема дебайеризации (восстановления цвета) выходит за рамки этой статьи, но просто знайте, что чем больше пикселей «накрыты» одним цветом, тем сложнее восстановить исходный цвет.
Поэтому в дешевых смартфонах никто даже не пытается этого делать и маленькие пиксели одного цвета просто складываются в один «большой пиксель».
Алексей, главред Deep-Review
P.S. Не забудьте подписаться в Telegram на первый научно-популярный сайт о мобильных технологиях — Deep-Review, чтобы не пропустить очень интересные материалы, которые мы сейчас готовим!
Как бы вы оценили эту статью?
Нажмите на звездочку для оценки
Внизу страницы есть комментарии.
Напишите свое мнение там, чтобы его увидели все читатели!
Если Вы хотите только поставить оценку, укажите, что именно не так?