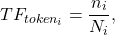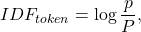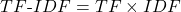Что такое бинарный вектор

Что такое бинарный вектор

Обработка естественного языка или NLP (Natural Language Processing) занимается применением алгоритмов Machine Learning для текстовых данных. Как правило, модели машинного обучения работают с числами. В этой статье поговорим о 4-х наиболее применяемых методах для перевода текстов в числовые тензоры.

Основные термины NLP: корпус, документ, токен, словарь

Сначала текст разбивается на текстовые единицы (токены), например, символы, слова, словосочетания, предложения, абзацы и т.д. Чаще всего разбивают на слова. Токены образуют словарь, который может быть отсортирован по алфавиту.
Также в NLP применяются термины «документ» и «корпус». Документ – это совокупность токенов, которые принадлежат одной смысловой единице. В качестве документа может выступать предложение, комментарий или пост пользователя. Корпус – это генеральная совокупность всех документов.
Рассмотрим пример. Допустим имеется два предложения: “Пес сел на пень”, “Кот сел на ель”. Выберем в качестве токенов слова, тогда получится следующий словарь:

и два документа, которые составляют корпус:

В последующих методах кодирования слов мы также будем использовать два этих предложения в качестве примера.

1. Прямое кодирование

Прямое кодирование (one-hot encoding) считается самым простым способом преобразования токенов в тензоры и выполняется следующим образом:

С нашими предложениями это выглядит так:

Проблемой прямого кодирования является размерность. Каждое предложение состоит всего из 4 слов, но в итоге получилась большая матрица для каждого документа. Количество строк регулируется словарем, поэтому чем больше слов в словаре, тем больше будет матрица.

2. Bag of words

В отличие от прямого кодирования, мешок слов (Bag of words) выделяет вектору весь документ, и каждый элемент кодируется 1 по порядку следования слов в словаре:

Bag of words решает проблему размерности по одной оси. Количество строк определяется количеством документов. Однако, этот метод не учитывает важность того или иного токена, ведь одно слово может повторятся по несколько раз. В этом случае пригодится альтернативный способ, рассмотренный далее.

3. TF-IDF

TF-IDF состоит из двух компонентов: Term Frequency (частотность слова в документе) и Inverse Document Frequency (инверсия частоты документа). Они считаются следующим образом:

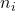
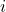
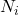
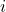
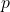
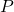
где — сколько раз встречается токен в -ом документе,
— общее количество токенов в -ом документе,
— количество документов, в которых встречается токен,
— общее количеств документов.
В конечном счете, TF-IDF – это произведение TF на IDF:

Стоит отметить, что TF считается для токенов документа, тогда как IDF – токенов всего корпуса. Итак, у нас имеется 2 документа, в каждом из которых оказалось по 4 слова. В этом случае вычисления будут следующими:

Вычисления TF-IDF

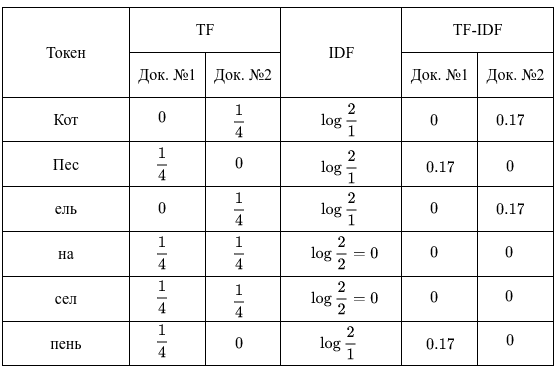
В результате получили для 1-го документа такие важные слова, как “Пес” и “пень”, для 2-го — “Кот” и “ель”. В TF-IDF редкие слова и слова, которые встречаются во всех документах, несут мало информации. Кроме того, IDF можно считать и другими способами, например, в Python-библиотеке Scikit-learn этот параметр гибко регулируется.

4. Word Embeddings

Все вышерассмотренные NLP-методы отличаются следующими недостатками:

На практике все чаще используется word embeddings – векторное представление слов. Векторы можно складывать, вычитать, сравнивать. Например, можно ли сложить слова “Король” и “Женщина”? Можно предположить, что будет “Королева”. А можно ли сравнить близость слов “мужчина”, “мальчик”, “девочка”? Напрашивается, что “мужчина” и “мальчик” стоят ближе друг к другу. На изображении показано, как это выглядит графически:

Векторное пространство слов

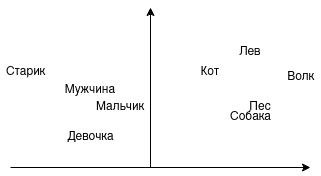
В этом примере на одной стороне животные, на другой люди. Со стороны животных возможен переход от домашних к диким или от псовых к кошачьим. Со стороны людей возможен переход по полу и возрасту. Именно так и работают word embeddings, представляя слова (токены) в векторы.
Самой распространенной реализацией векторного представления слов является Word2vec. Архитектура Word2vec подразделяется на два вида — Skip-gram и Continuous Bag of Words (CBOW).
Skip-gram получает на вход одно слово и предсказывает подходящий контекст. Например, предсказываем контекст к слову “Пес”, он может выглядеть так:

В свою очередь, CBOW пытается угадать слово, исходя из контекста. Например, следующее слово в предложении “Кот сел на […]” может быть следующим:

Контекст для word embeddings является очень важным. Юридические документы отличаются от комментариев в социальных сетях, поэтому и результат может быть разным.

В следующей статье поговорим об первичной обработке текстов. А получить практические навыки работы с текстами в NLP на реальных задачах Data Science вы сможете на наших курсах по Python в лицензированном учебном центре обучения и повышения квалификации ИТ-специалистов в Москве.

Источник

Примеры 1

Логические высказывания и функции. Таблицы истинности

БУЛЕВА ЛОГИКА

Двоичные (булевы) векторы

Пример 1. Найти порядковый номер булева вектора`b = (1,0, 0, 1, 0, 1) в десятичной системе счисления.

Решение. Устраняя запятые в векторе, получим двоичную запись 100101. Переводя ее по правилу 2.1.1 в десятичную систему, получим:

Ответ: десятичный порядковый номер вектора (1,0, 0, 1, 0, 1) равен 37.

Пример 2. Упорядочить по возрастанию порядковых номеров булевы векторы длины 6: (1, 0, 1, 0, 1, 1, 0), (0, 1, 1, 0, 1, 0, 0), (0, 0, 1, 1, 0, 1, 0).

Решение. Определяя, как в примере 1, десятичные порядковые номера наборов, получим для них:

(1, 0, 1, 0, 1, 1, 0)↔1010110₂ = 86₁₀, (0, 1, 1, 0, 1, 0, 0)↔110100₂ = 52₁₀, (0, 0, 1, 1, 0, 1, 0)↔11010₂ = 26₁₀.

Искомый порядок получим, располагая векторы в порядке возрастания их номеров: (0,0,1,1,0,1,0), (0,1,1,0,1,0,0),(1,0,1,0,1,1,0).

Практические задания.

1. Найти порядковый номер двоичного вектора (0, 0, 1, 0, 1, 1, 0) в десятичной системе счисления.

2. Упорядочить по убыванию порядковых номеров двоичные векторы длины 5:

(0, 1, 0, 1, 0), (1, 1, 0, 1, 0), (1, 0, 0, 1, 0), (0, 0, 1, 1, 0).

Логика как наука о формах и законах мышления возникла в Древней Греции. Вначале она была составной частью риторики – науки убеждения. Новый импульс развитие логики получило в ХVIII–ХIХ веках, когда в результате развития естественных наук выявилось сходство применяемых в них методов рассуждений. Однако широкое использование математических методов началось только в середине ХIХ века после применения в логике шотландским математиком Дж. Булем математических обозначений.

С современной точки зрения основной задачей логики является выяснение правильности логических рассуждений безотносительно к предмету рассуждения.

Объектами логики как математической дисциплины являются высказывания. Это любые утверждения на естественных или формальных языках, о которых имеет смысл говорить, истинны они либо ложны.

Истину обозначают И, ложь – через Л (англ.- Т(true), F (false)). При математическом обозначении И заменяют на 1, Л – на 0.

Простое высказывание выражает одну законченную мысль. Если высказывание всегда истинно (равно 1), либо всегда ложно (0), то его называют константой. Логические константы обычно обозначают маленькими или большими начальными латинскими буквами, при которых также используют нижние индексы. Например: a, b, c, A, B, b₁, c₂, A₂.

Если высказывание может принимать оба логических значения (и 0, и 1), то его называют переменным(логической переменной). Логические переменные обозначают средними латинскими буквами (с индексами и без них), например: x, у, z, Х, Y, Z. x₁, z₂, Y₃.

3) х =«треугольник является прямоугольным»― булева переменная, поскольку х может принимать значения и 0 и 1,

4) «дом большой» ― фраза не является высказыванием, поскольку выражает субъективное мнение и не ясно, какой дом можно считать большим.

Наряду с фразами на естественном языке, логические константы и переменные могут быть заданы арифметическими условными выражениями, зависящими от числовых вещественных констант и переменных. Например, (x 2 +y 2 2 +y 2 ³10) и другие. Рассмотрим их истинность.

Условие (x 2 +y 2 2 +y 2 ³10) ложно, так как 1 2 +2 2 =5 2, а условие (x 2 +y 2 ³10) истинно, так как 4 2 +2 2 = 20 > 10. Т.е. (x 2 +y 2 ³10) – логические переменные.

Допустим, задан некоторый набор логических переменных, обозначенных, на­пример, x, у, z. Отображение (правило) f, сопоставляющее каждому возможному набору значений переменных (x, у, z) свое логическое значение (0 или 1), называют логической функцией. Обозначается она как f(х, у, z).

Пример 2.Зададим функцию f, зависящую от двух переменных х,у списком, в котором перечислены все возможные логические значения для на­боров переменных (х,у) и соответствующие им значения f:

По числу переменныхn логические функции называют одноместными (n=1), двухместными (n=2) и т.д.

Простейшим способом непосредственного задания функций является табличный, при котором все возможные значения наборов переменных располагают по возрастанию их порядковых номеров (в лексикографическом порядке), а значения функции f поме­щают в отдельном столбце, который называют вектором истинности функции. Всю конструкцию называют таблицей истинности функции. Для рассмотренной в примере 2 функции двух переменных f(х,у) таб­лица истинности имеет вид:

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Интегрирующие и челночные (бинарные) векторы

Векторы, пригодные для клонирования ДНК в бактериях, отличающихся от E. coli, должны обладать всеми характерными чертами, которые были отмечены выше. От только что рассмотренных они отличаются главным образом тем, что содержат природные или искусственные генетические элементы, функционирующие в новых клетках-хозяевах.

Интегрирующие векторы грамположительной бактерииBacillus subtilis. B. subtilis, как и E. coli, является излюбленным объектом генной инженерии. Это связано с тем, что B. subtilis – непатогенный микроорганизм, многие штаммы которого широко используются в микробиологической промышленности для производства биологически активных соединений и пищевых веществ. В отличие от E. coli B. subtilis способна секретировать белки и пептиды, что облегчает их очистку и дальнейшее использование. Большинство векторов для клонирования ДНК в клетках B. subtilis создано на основе плазмид других видов бацилл, а также Staphylococcus aureus и бактерий рода Streptococcus.

Рис. II.11. Челночный вектор pFH7 (а) и экспрессирующий вектор pPR-TGATG-1 (б)

Обозначено расположение генов и уникальных сайтов рестрикции

Основным свойством интегрирующих векторов является их способность стабильно встраиваться в геном клетки-хозяина. Это становится возможным благодаря наличию в таких векторах последовательностей нуклеотидов, гомологичных последовательностям геномной ДНК. В результате функционирования общей системы рекомбинации происходит объединение хромосомной и плазмидной ДНК интегрирующего вектора, которое приводит к стабильному включению всей векторной плазмиды в хромосому. Примером такого интегрирующего вектора служит плазмида pFH7 B. subtilis (рис. II.11,а). Векторная плазмида содержит фрагмент ДНК умеренного бактериофага SPb и после попадания в клетки B. subtilis, лизогенные по данному бактериофагу, эффективно интегрируется в профаг. Поскольку плазмида содержит ген устойчивости к хлорамфениколу cat, клетки приобретают этот признак. Индукция профага приводит к образованию фаговых частиц, трансдуцирующих такую плазмиду и ассоциированный с ней признак устойчивости к хлорамфениколу. Интеграция плазмиды SPb в бактериальную хромосому происходит по механизму гомологичной рекомбинации с участием гена recE.

Способность к интеграции в бактериальную хромосому обнаруживают и другие плазмиды, содержащие фрагменты хромосомной ДНК клеток-хозяев, что продемонстрировано, в частности, для плазмид E. coli и Streptococcus pneumoniae.

Интегрирующие векторные системы, в которых используется тот же принцип гомологичной рекомбинации, разработаны и для эукариотических клеток, включая клетки животных и растений. В конце концов, такие работы привели к развитию целого направления исследований по созданию трансгенных животных и растений, стабильно наследующих и экспрессирующих гены, искусственно введенные в их геном. О некоторых важных следствиях этого направления исследований, включая генотерапию, речь пойдет в главе 10.

Наличие феномена гомологичной рекомбинации между хромосомной ДНК клетки-хозяина и векторной ДНК, содержащей гомологичные хромосомной ДНК последовательности нуклеотидов, приходится учитывать при получении соответствующих генно-инженерных конструкций. Такая неконтролируемая рекомбинация в большинстве случаев нежелательна, так как может приводить к потере или структурным перестройкам клонированных фрагментов ДНК. Для того чтобы свести последствия этого явления к минимуму, используют специальные штаммы клеток-хозяев, в которых общая система рекомбинации не функционирует, например вследствие мутационной инактивации гена recA E. coli или recE B. subtilis.

Челночные векторы. Интегрирующая плазмида pFH7 (см. рис. II.11,а) дает возможность проиллюстрировать еще один важный принцип, широко используемый при конструировании векторных систем в генной инженерии. Эта плазмида получена путем объединения двух репликонов, один из которых берет начало от плазмиды pC194 B. subtilis, а другой – от плазмиды pBR322 E. coli, что дает возможность вектору существовать и стабильно реплицироваться как в клетках E. coli, так и B. subtilis. Такие векторы, способные реплицироваться в клетках-хозяевах разных биологических видов, называют челночными, или бинарными векторами.

Принципы конструирования и функционирования челночных векторов одинаковы, они должны включать в себя репликоны тех генетических систем, в которых будет происходить репликация челночного вектора. При этом используются области начала репликации генетических элементов, которые автономно существуют во внехромосомном состоянии в природных условиях. Так, обсуждавшийся выше интегрирующий вектор pFH7 B. subtilis обладает свойствами челночного вектора, поскольку для его конструирования использованы репликоны двух видов бактерий. Более эффектными примерами челночных векторов являются плазмидные ДНК, способные реплицироваться в клетках высших (животных и растений) и низших организмов. Необходимость использования челночных векторов в генной инженерии связана с тем, что наработку в препаративном количестве векторной ДНК для проведения генно-инженерных манипуляций удобнее проводить в бактериальных клетках, тогда как получение биологически активных продуктов клонированных генов высших организмов во многих случаях возможно только в клетках своего или близкого вида, в которых эти гены экспрессируются в природных условиях, т.е. в своем обычном генетическом окружении (подробнее см. раздел 7.6).

Источник

Двоичные (булевы) векторы

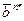
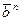
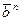
Двоичный вектор является обратным (инвертированным) к , если он образован из заменой всех нулей единицами, а единиц – нулями.

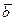
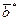
Например, если = (0,1,1,1,0,1), то = (1,0,0,0,1,0).

Пример 1.Найти порядковый номер булева вектора 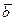= (1,0,0,1,0,1) в десятичной системе счисления.

Решение. Устраняя запятые в векторе, получим двоичную запись 100101₂. Переводя ее по правилу 2.1.1 в десятичную систему счисления, получим:

100101₂ =1×2 5 +1×2 2 +1×2 0 =32₁₀ +4₁₀ +1₁₀ =35₁₀.

Ответ: десятичный порядковый номер заданного булева вектора равен 35₁₀.

В качестве меры близости булевых векторов используют расстояние Хэмминга.

Пример 8. r(100011, 110011)=1, r(0101, 1010)=4.

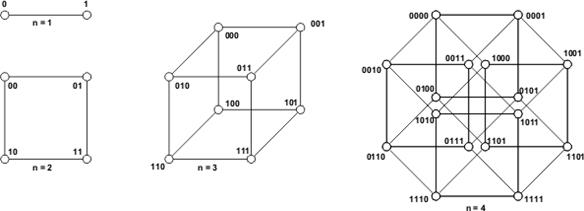
Рассмотрим наиболее употребительные геометрические интерпретации булевых n – мерных векторов.

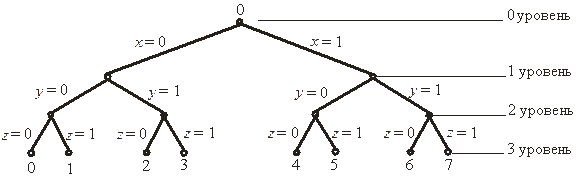
В качестве примера рассмотрим полное множество 3-мерных двоичных векторов, расположенных в лексикографическом порядке:

Рис. 4.1. Бинарное дерево Т 3

Вопросы для проверки знаний.

1. Есть ли принципиальное различие правил выполнения сложения и вычитания в десятичной системе счисления и других системах с постоянными основаниями?

2. Какой формат компьютерного представления чисел называют беззнаковым целым числом?

3. Какой формат компьютерного представления чисел называют целым числом со знаком?

4. Какой способ компьютерного представления целых чисел называют прямым кодом?

5. Какой способ компьютерного представления целых чисел называют дополнительным кодом?

6. Для каких целых чисел прямой код совпадает с дополнительным кодом?

7. Может ли целое число занимать в электронной памяти а) 4 бита, б) 6 бит, в) 8 бит, г) 10 бит?

8. По каким правилам осуществляется перевод беззнаковых байтовых целых чисел из прямого кода в дополнительный и обратно?

9. По каким правилам осуществляется перевод байтовых целых чисел со знаком из прямого кода в дополнительный и обратно?

10. В каких случаях вычитание байтовых беззнаковых целых чисел дает результат в прямом коде, а в каких – в дополнительном?

11. Что называют двоичным (булевым) n-мерным вектором?

12. Какую операцию называют инвертированием булевого вектора?

13. Какие числа называют порядковыми номерами булевых векторов?

14. Что называют лексикографическим порядком двоичных векторов?

Источник

Линейная алгебра для разработчиков игр

Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.

Зачем нам линейная алгебра?

Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.

Что такое вектор?

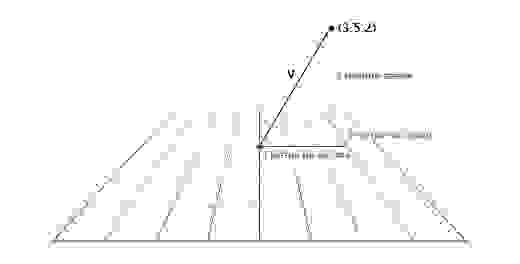
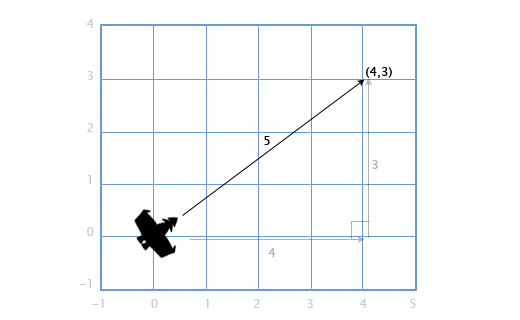
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.

Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.

Сложение векторов

Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:

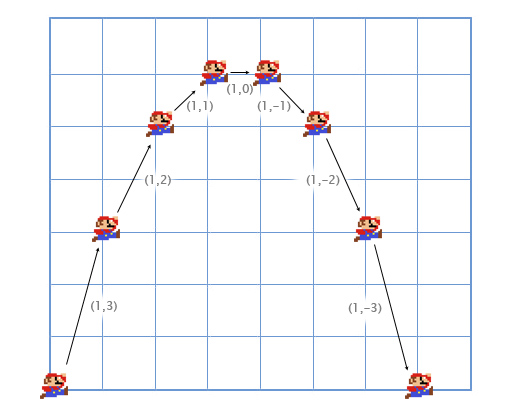
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.

Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.

Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.

Вычитание векторов

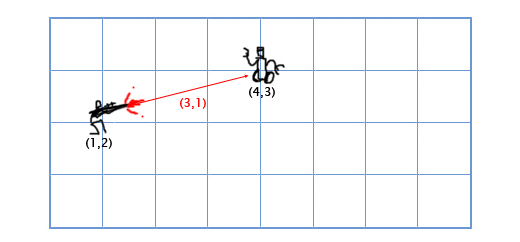
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:

(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).

Умножение вектора на скаляр

Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:

0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).

Длина вектора

Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.

Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2

В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).

Итак, скорость нашего корабля равна:

|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5

Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )

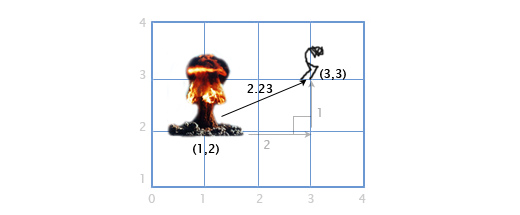
Расстояние

Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23

Нормализация

Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:

(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1

Скалярное произведение векторов

Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе

(a1, a2) • (b1, b2) = a1b1 + a2b2

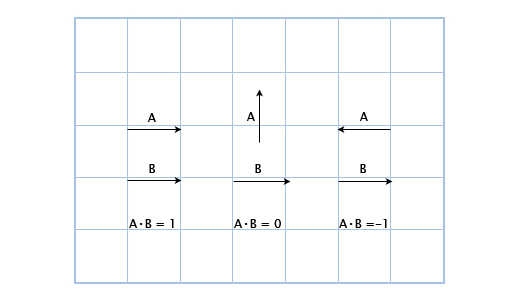
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:

Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.

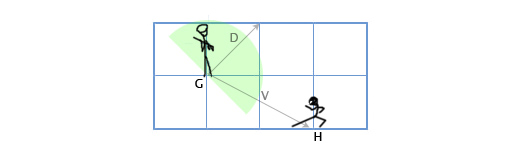
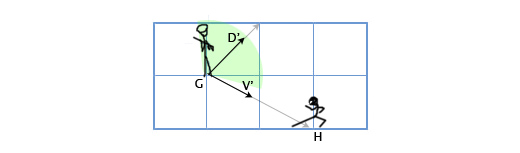
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:

Так как единица больше нуля, то главный герой находится в поле зрения стражника.

Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:

Где Θ (произносится как «theta») — угол между векторами A и B.

Это позволяет нам найти Θ (угол) с помощью выражения:

Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:

Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.

Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72

Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.

Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:

Векторное произведение

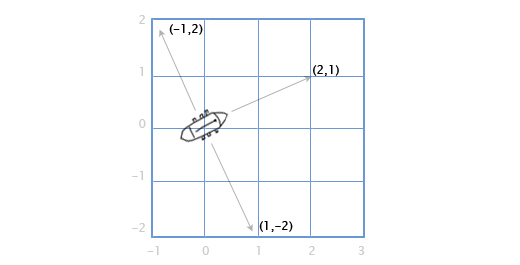
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?

А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
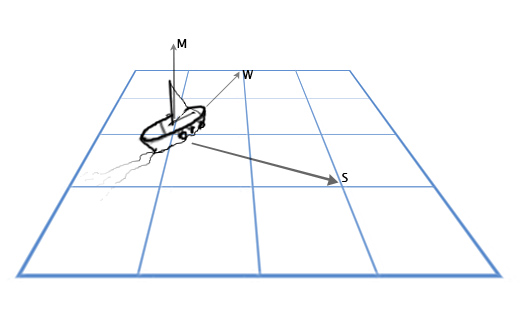
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».

Для решения этой задачи мы используем векторное произведение: S = M x W.

Подставим теперь нужные нам значения:

Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.

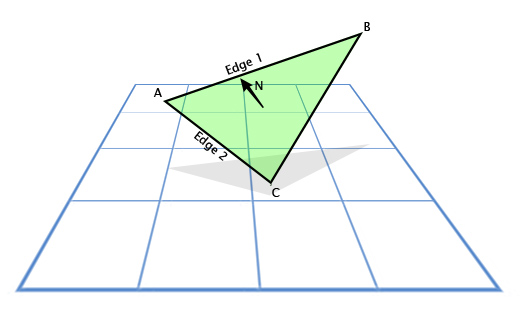
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.

Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».

Вот так это выглядит в коде:

В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.

Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).

Для начала изучим «строительные блоки» матрицы преобразований.

Базисный вектор

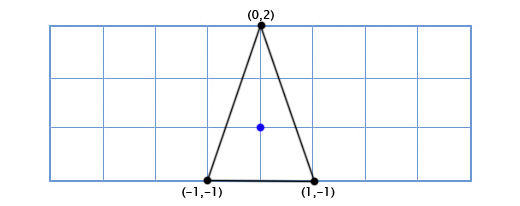
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:

Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:

Применяя эту функцию ко всем трём точкам, мы получим следующую картину:

Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).

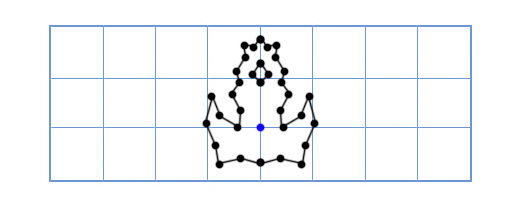
Пусть теперь наш корабль выглядит вот так:

Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»

Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.

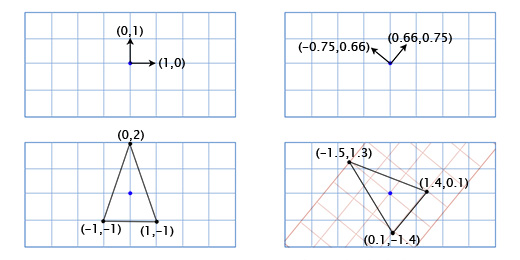
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.

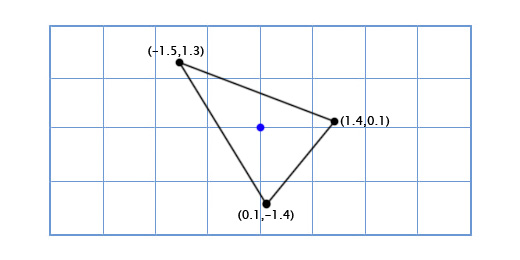
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:

Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:

0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)

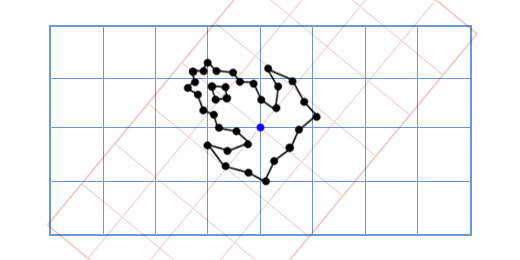
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.

Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:

Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.

Матрицы

Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:

Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:

Будучи записанным по-другому, это выражение выглядит так:

Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:

Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:

Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:

Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.

К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:

И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:

Теперь, когда мы перемножаем их, мы получаем:

(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)

Что, в свою очередь, может быть записано как:

Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.

Трехмерные матрицы

Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:

Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:

И добавляем единицу [1] в вектор, как здесь:

Вращение в двухмерном пространстве

Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:

Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:

(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))

Затем, мы включаем координатную ось Y (0, 1). Получим:

(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))

Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:

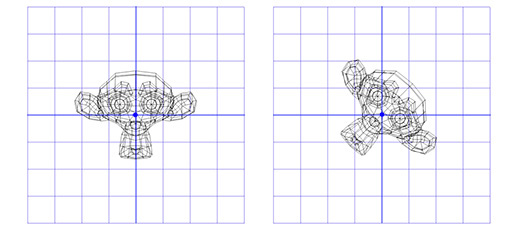
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.

Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
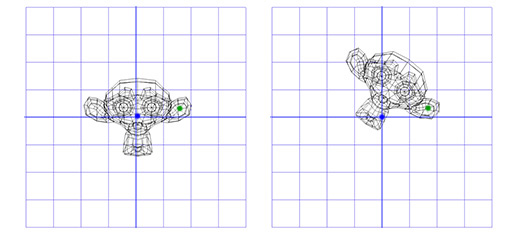
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:

Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.

Теперь рассмотрим трёхмерное вращение.

Трёхмерное вращение

Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:

Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.

То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?

Вращение, определяемое осью и углом (Axis-angle rotation)

Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.

Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?

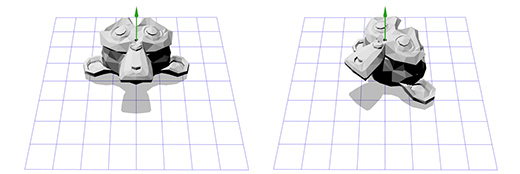
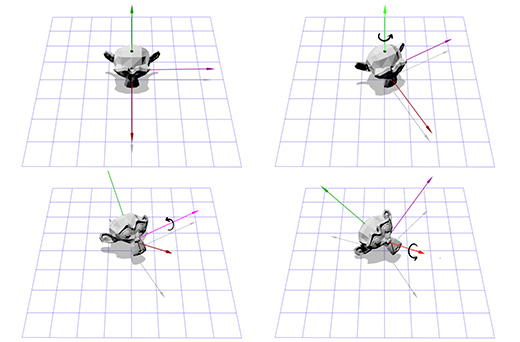
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:

Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.

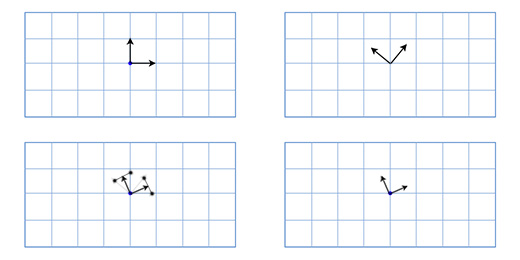
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.

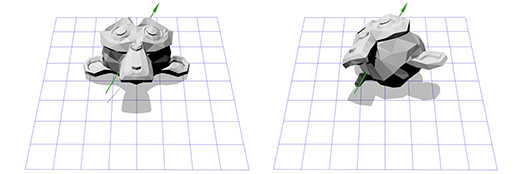
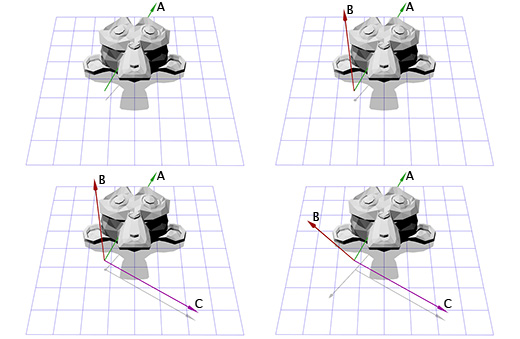
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.

Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.

На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:

Тут показана иллюстрация для каждого шага:

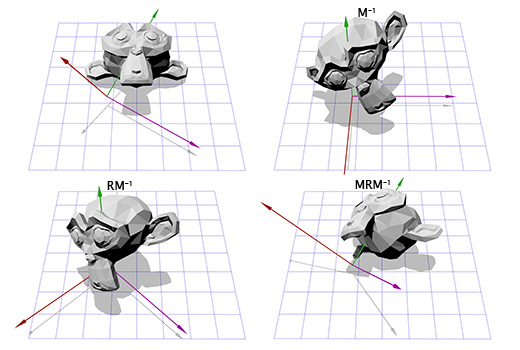
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.

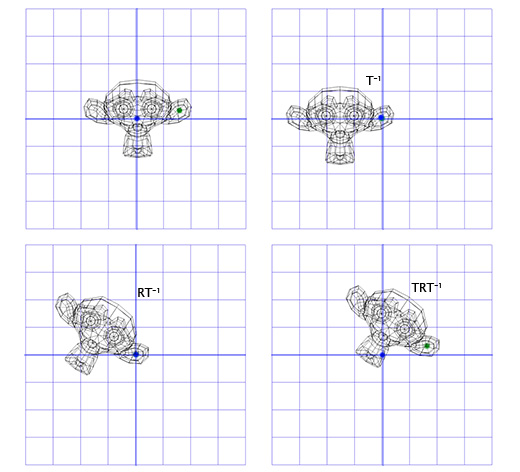
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.

Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.

Эйлеровские углы

Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.

Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).

Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.

Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.

Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.

Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?

Вращение с помощью матриц

Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:

Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.

Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).

Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.

Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.

Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.

Кватернионы

Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.

Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.

Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.

Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.

Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.

«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.

Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.

Источник