Что такое бинарная логика
Замена двоичной логики — увеличит ли это производительность?
Наверняка на хабре уже немало постов на эту тему. Тем не менее, я попытаюсь рассказать свою точку зрения на всё это…
Однажды я прочитал в интернете про троичную систему счисления и заинтересовался. Меня мучил вопрос, а нельзя использовать в основе компьютера симметричную троичную систему счисления (СС), и даже вдруг это увеличит производительность компьютера? Мне казалось, что это возможно, и я жаждал это проверить.
Информация:
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3. Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры <0,1,2>, а в симметричной троичной системе счисления знаки <−,0,+>, <−1,0,+1>.
У некоторых людей эта логика вызывает затруднения. Они говорят, например, приведите пример подобной логики в жизни.
Человек, немного подумавший над этой логикой поймет, что она более жизненна чем двоичная. Обычный пример троичной логики в жизни связан с постоянным током: ток движется в одну сторону, в другую сторону, его нет.
Оказалось, что симметричная троичная система счисления использовалась давным-давно для решения «задачи о гирях», использовалась в компьютере Сетунь, построенном в 50-е годы в МГУ. С 2008 года в университете « California Polytechnic State University of San Luis Obispo» функционирует цифровая компьютерная система TCA2, основанная на троичной системе счисления. 
В чем же плюсы троичной СС над двоичной? Рассмотрим эти плюсы:
Меньше разрядов
Емкость
Экономичность системы счисления
Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас тем экономичнее система. По затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. Обозначим p основание системы счисления, n количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел которое при этом можно записать будет равно pn/p.
Мы рассмотрели троичную арифметику, теперь затронем логику:
В чем же проблемы двоичной логики?
1.Мощности компьютера, основанного на двоичной логике, не всегда хватает. Приведем пример. Одна из наиболее сложных систем защиты – криптосистема RSA. Вскрытие шифра RSA с длиной ключа 1024 бита (такая длина часто используется в информационных системах) займет в лучшем случае — при проведении распределенных вычислений на тысячах мощных ПК — не менее пятнадцати лет, а к тому времени данная система шифровки перестанет быть востребованной.
Докажем математически какая система счисления будет наилучшей для максимальной мощности и емкости памяти. Для этого рассмотрим функцию f(p)=p^(n/p), в которой p – основание системы счисления, а n – количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел, которое при этом можно записать, будет равно pn/p
f(p)=p^(n/p)
Для того, чтобы определить максимальное значение функции, найдем ее производную:
ln f = ln p^(n/p)
ln f =n/p* ln p
. (Я не буду приводить здесь всю математику)
n*p^(n/p-2) никогда не будет равно 0 => (1 — ln p)=0, ln p = 1, p = e
e = 2,71, а ближайшее целое число к нему – это три.
Значит, в этом плане лучшая система с целочисленным основанием — троичная.
Самое вкусненькое — рассмотрим троичные логические операции:
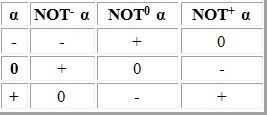
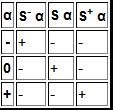
1.Отрицание
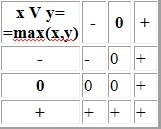
2.Конъюнкция — логическое И
3.Дизъюнкция — логическое ИЛИ
4.Операция Выбора. Эта операция существует только для троичной логики. Таблица истинности каждой из этих трёх операций содержит везде „-“, кроме единственного значения, которое ею можно выбрать.
5.Модификация. Полное название этих одноместных операций: увеличение на единицу по модулю три (INC) и уменьшение на единицу по модулю три (DEC). Увеличение на единицу по модулю три – это циклическое прибавление единицы. 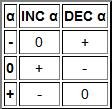
Здесь видны и прежде знакомые вам логические операции из двоичной логики, но добавились и новые…
Квантовые компьютеры
Квантовый компьютер — вычислительное устройство, работающее на основе квантовой механики. Квантовый компьютер принципиально отличается от классических компьютеров, работающих на основе классической механики.
Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма RSA. До сих пор этот алгоритм считается сравнительно надёжным, так как эффективный способ разложения чисел на простые множители для классического компьютера в настоящее время неизвестен. Для того, например, чтобы получить доступ к кредитной карте, нужно разложить на два простых множителя число длиной в сотни цифр. Даже для самых быстрых современных компьютеров выполнение этой задачи заняло бы больше времени, чем возраст Вселенной, в сотни раз. Благодаря алгоритму Шора эта задача становится вполне осуществимой, если квантовый компьютер будет построен.
Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит. Это устройство работает на кубитах — квантовых аналогах битов.
Но можно построить компьютеры не на битах, а на кутритах — аналогах трита в квантовом компьютере.
Кутрит (квантовый трит) — квантовая ячейка, имеющая три возможных состояния.
Подлинное новаторство метода Ланьона в том, что, используя в универсальных квантовых вентилях кутриты вместо кубитов, исследователи могут существенно снизить количество необходимых вентилей.
Ланьон утверждает, что компьютер, который в обычном случае использовал бы 50 традиционных квантовых вентилей, сможет обойтись всего девятью, если будет основан на троичном представлении.
Также, согласно некоторым исследованиям, использование кутритов вместо кубитов позволит упростить реализацию квантовых алгоритмов и компьютеров.
Итог:
В конечном итоге видно, что троичная симметричная система лучше двоичной системы в некоторых показателях, но не сильно выигрывает. Но с пришествием квантовых компьютеров троичные вычисления получили новую жизнь. Универсальные квантовые логические вентили — краеугольный камень новорожденных квантовых вычислительных систем — требует сотни вентилей для завершения одной полезной операции. Квантовый компьютер канадской компании D-Wave, анонсированный в прошлом году, состоит всего из 16 квантовых битов — кубитов — минимум, необходимый для управляемого вентиля «NOT». Использование в квантовом компьютере кутритов нужно было бы намного меньше вентилей для завершения одной операции. Я думаю, если бы началось производство и тестирование таких компьютеров, то результаты были бы лучше, чем у обычных компьютеров, вскоре началось бы массовое их производство, и про двоичные компьютеры все бы забыли…
Проблемы бинарной логики, или Почему ИИ — просто усовершенствованный калькулятор
Искусственный интеллект не защищен от ошибок. Ведь он — создание человеческого разума, а наше мышление — это скопище ошибок и заблуждений. Да, наши суждения часто ошибочны. Даже если мы очень стараемся судить объективно, мы всё равно обречены на стереотипное мышление и далеко идущие неаргументированные выводы. Однако ошибки ИИ вовсе не такие. Он ошибается не по причине субъективности, а из-за самой сути алгоритмического мышления. Во всём виновата бинарная логика.
Бинарная логика основана на двух утверждениях: истина (логическая единица ) или ложь (логический нуль ). Благодаря такому простому механизму возможно быстро и эффективно проводить вычисления. Чтобы машина могла понимать печатные символы и алфавит, используется кодировка ASCII (American Standard Code for Information Interchange). С ее помощью привычный человеку текст переводится в понятные машине нули и единицы.
Однако это не означает, что машина понимает мир и слова так же, как и мы. Нам приходится пользоваться бинарной логикой, чтобы общаться с машиной, но машина не может говорить с нами, пользуясь человеческими мыслительными процессами.
Мы не мыслим нулями, единицами и исключительно количественными категориями. Мы оперируем деталями, контекстами, разными измерениями, динамикой процессов, ценностями и богатством опыта.
Но самое интересное во всём этом, что бинарная логика — это вовсе не изобретение сумасшедших инженеров начала XX века. За бинарную логику стоит говорить спасибо Аристотелю.
Бинарная логика и сексизм Аристотеля
Что? Аристотелю? Отцу демократии и великому философу? За вот эту ущербную машинную логику?
Вообще да, именно ему и его теории дуализма. За 350 лет до нашей эры Аристотелю захотелось сделать мир проще и понятнее. За основу он взял пифагорейскую таблицу противоположностей, которая выглядела примерно так:
Конечность — бесконечность
Чёт — нечет
Единство — множество
Правый — левый
Покой — движение
Прямой — кривой
Добро — зло
и т. д.
Пифагор с помощью этой таблицы демонстрировал, что числа — это не про количество единиц, а про некую силу и вектор ее направления.
Аристотель посмотрел на нее и подумал: ведь разделение на противоположности работает и с людьми, и с животными, и с обществом. Кто-то занимает один полюс, а кто-то — другой. Кто-то прав, а кто-то виноват. Кто-то добр, а кто-то зол.
Аристотель соорудил на фундаменте дуализма иерархическую систему и снабдил ее собственными представлениями о носителях одной полярности (со значением «1») и другой (со значением «0»). Ну, к примеру:
1 = истина = разум = правый = мужчина
0 = ложь = чувства = левый = женщина
Вот такой сексизм 2000-летней давности.
Если бы Аристотель прислушивался к своим предшественникам, Сократу и Платону, он бы, возможно, не был бы так уверен в подчиненном положении женщин и ущербности их разума, и право голоса женщины получили бы не в начале XX века, а гораздо раньше.
В диалоге Платона «Пир» Сократ с большим уважением отзывался о мудрости жрицы Диотимы из Мантинеи, а в Книге 5 «Государства» он говорит, что управлять городом с равным успехом может и мужчина, и женщина.
Тем не менее именно аристотелевская логика легла в основу западной мысли и продолжает пускать ростки стереотипов и предубеждений.
Бинарная логика Декарта и китайская ошибка Лейбница
Эстафетную палочку Аристотеля перехватили в XVII–XVIII веках Декарт и Лейбниц. Декарт, изобретатель афоризма «Я мыслю, следовательно, я существую», зародил идею о том, что любой субъект имеет только ту ценность, которую ему приписывает наблюдатель.
Кроме того, рассуждения Декарта продолжали тенденцию отделения разума от телесных и чувственных проявлений: в «Размышлениях о первой философии» ученый отнес разум к миру идеального, а тела и чувства — к миру материального, где эти два мира не пересекаются.
Плюс Декарт был разочарован несистемными методами, которыми пользовались математики в его время и разработал дедуктивно-индуктивную логику, основы которой изложил в «Рассуждениях о познании». Математика в представлении Декарта должна иметь крепкий фундамент, и в качестве него он использовал аристотелевскую бинарную логику (1 = истина = действительно, 0 = ложь = недействительно), только упаковал ее в древовидную структуру. Теперь она используется в нейросетях при обработке естественных языков.
Немецкий мыслитель и юрист Лейбниц, создатель математического анализа (одновременно с Ньютоном), разработал бинарную модель счисления как быстрый способ получать готовые расчеты.
Интересно, что Лейбниц был ярым китаистом. В 1703 году священник Буве высылает мыслителю копию «Книги перемен» («И Цзин»), древний китайский философский текст. Книга состоит из 64 гексаграмм, в которых Лейбниц уловил сходство с собственными бинарными таблицами и пришел в восторг.
В одних гексаграммах Лейбниц увидел нули, а в других — единицы, что утвердило его в мысли о том, насколько бинарная логическая система универсальна и всеобъемлюща.
Вот только Лейбниц ошибся: во-первых, он рассматривал гексаграммы, перевернув их вверх ногами. Во-вторых, он не учел, что каждая гексаграмма соответствовала определенному описанию на китайском. В третьих, каждая из них представляла собой запись двух противоборствующих энергий — положительной и негативной, инь и ян.
В любом случае и Лейбниц, и Декарт сделали свой вклад в развитие западного мышления, замкнутого в противоестественной дуальной логике.
Бинарная логика сегодня
На бинарной логике построены все современные системы данных. Нулями и единицами пронизаны любые действия, которые производятся сегодня в цифровом поле. Вот, например:
Свайп вправо = 1, свайп влево = 0
Поставили лайк =1, не поставили = 0
Кажется, пользователь испытывает положительные эмоции = 1, отрицательные = 0
Группируем объекты по красному цвету: яблоко = 1, апельсин = 0
Машина лишь регистрирует, какой выбор сделал человек, и дает соответствующую реакцию, выбирая из двух вариантов.
Бинарная логика не предоставляет пространства для моделирования причин принятия подобных решений. Мы собираем черно-белые данные, сортируя их по оттенкам серого, когда мир вокруг — это целая радуга.
Окружающий нас мир не терпит бинарности. Частицы в квантовой суперпозиции могут быть одновременно и нулем, и единицей. Взаимосвязи между явлениями и свойствами богаче и неоднозначнее, чем чёт и нечет.
Бинарностью легко оперировать, но в таком случае нам стоит смириться с тем, что искусственный интеллект так и останется усовершенствованной моделью калькулятора.
Двоичная логика
Двоичная логика
Двоичная логика (двузначная логика) — это логика, основанная на двух утверждениях. Истина (логическая единица) и ложь (логический нуль). Из-за простоты реализации получила широкое распространение в вычислительной технике. В вычислительной технике разделяют положительную (истина=1, ложь=0) и отрицательную (истина=0, ложь=1) логику.
В простейшей Булевой алгебре есть только два элемента, 0 и 1, и следующие операции:
Содержание
Нульарные
Нульарные операции суть константы. В двоичной логике ими являются логический нуль (0) и логическая единица (1).
Унарные
| X | НЕ X |
|---|---|
| 0 | 1 |
| 1 | 0 |
Бинарные
|
|
Двоичный полусумматор
| X | Y | S=X  Y= Y= f(2,1,06)10(x,y) | P=X&Y= f(2,1,08)10(x,y) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Двоичный полувычитатель
| X | Y | R=X  Y= Y= f(2,1,06)10(x,y) | Z(N+1)= f(2,1,04)10(x,y) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Тринарные
|
|
Двоичный сумматор
| X | Y | P(N-1) | S=X  Y Y  Z= Z= f(3,1,150)10(x,y,z) | P(N+1)= f(3,1,232)10(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Двоичный вычитатель
| X | Y | Z(N-1) | R=X  Y Y  Z= Z= f(3,1,150)10(x,y,z) | Z(N+1)= f(3,1,216)10(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
См. также
Ссылки
Полезное
Смотреть что такое «Двоичная логика» в других словарях:
двоичная логика — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN binary logic … Справочник технического переводчика
двоичная логика — dvejetainė logika statusas T sritis automatika atitikmenys: angl. binary logic; two valued logic vok. binäre Logik, f; Binärlogik, f; zweiwertige Logik, f rus. двоичная логика, f pranc. logique binaire, f … Automatikos terminų žodynas
Бинарная логика — Двоичная логика (двузначная логика) это логика, основанная на двух утверждениях. Истина (логическая единица) и ложь (логический нуль). Из за простоты реализации получила широкое распространение в вычислительной технике. В вычислительной технике… … Википедия
Комбинационная логика — В теории цифровых устройств комбинационной логикой (комбинационной схемой) называют логику функционирования устройств комбинационного типа. У комбинационных устройств состояние выхода однозначно определяется набором входных сигналов. Это отличает … Википедия
Секвенциальная логика — Секвенциальная логика это логика памяти цифровых устройств. Название «секвенциальная» восходит к англ. sequential. Соответствующая логика может именоваться также как последовательностная, хотя последний термин по преимуществу употребляется… … Википедия
ТЕОРЕТИКО-МНОЖЕСТВЕННАЯ ЛОГИКА — (теоретико множественная логика п р е д и к а т о в) – логика, трактуемая с т. зр. теории множеств. К Т. м. л. в широком с м ы с л е можно отнести любые интерпретации логич. исчислений, в основу к рых положено объемное, экстенсиональное понимание … Философская энциклопедия
отрицательная логика — Двоичная логическая система, в которой логической «I» соответствует более низкий уровень сигнала, чем логическому «0». [ГОСТ Р 50304 92] Тематики системы для сопряж. радиоэлектр. средств интерфейсные … Справочник технического переводчика
положительная логика — Двоичная логическая система, в которой логической «I» соответствует более высокий уровень сигнала, чем логическому «0». [ГОСТ Р 50304 92] Тематики системы для сопряж. радиоэлектр. средств интерфейсные … Справочник технического переводчика
отрицательная логика — 7 отрицательная логика: Двоичная логическая система, в которой логической «I» соответствует более низкий уровень сигнала, чем логическому «0» Источник: ГОСТ Р 50304 92: Системы для сопряжения радиоэлектронных средств интерфейсные. Термины и… … Словарь-справочник терминов нормативно-технической документации
положительная логика — 8 положительная логика: Двоичная логическая система, в которой логической «I» соответствует более высокий уровень сигнала, чем логическому «0» Источник: ГОСТ Р 50304 92: Системы для сопряжения радиоэлектронных средств интерфейсные. Термины и… … Словарь-справочник терминов нормативно-технической документации