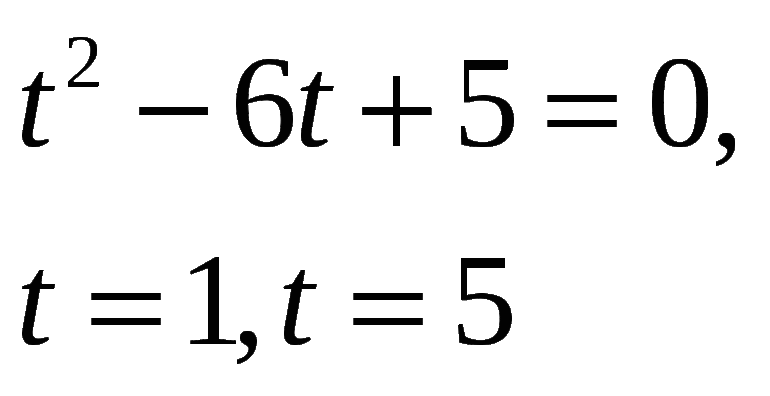Что такое биквадратное уравнение

Как решать биквадратное уравнение: видео

В прошлых уроках мы научились решать квадратные уравнения. Для этого потребовалось ввести новый математический объект — дискриминант. Если вы не помните, что это такое, рекомендую вернуться к уроку «Как решать квадратные уравнения».

Для начала определение, что вообще такое биквадратное уравнение — это любое выражение, где переменная присутствует только в 4-ой и во 2-ой степени.

Как считать такие биквадратные конструкции? Схема состоит из пяти шагов. Все шаги очень легкие и очень быстрые:

5)решаем полученные уравнения и находим иксы.

Реальные задачи

Пример № 1

Давайте посмотрим, как эта схема работает на настоящих биквадратных уравнениях.

Решаем первую задачу:

Вводим новую переменную и переписываем:

Это обычное квадратное уравнение, посчитаем его с помощью дискриминанта:

Это хорошее число. Корень равен 3.

Пример № 2

Переходим ко второму примеру:

Тут я не буду подробно все расписывать. Давайте решать так, как бы мы делали это в классе.

Тогда у нас выйдет:

Пример № 3

Переходим к последнему биквадратному уравнению:

Опять же вводим замену:

Давайте умножим обе стороны на 4, чтобы избавиться от дробных коэффициентов:

Корень из дискриминанта равен трем:

Второй вариант чуть посложнее:

Мы получили снова четыре корня:

Вот так решаются все биквадратные уравнения. Конечно, это не самый быстрый способ, зато он самый надежный. Попробуйте самостоятельно прорешать такие же примеры, как и в этом видео. В ответе значения иксов нужно записывать через точку с запятой — вот так, как я записывал. На этом урок закончен. Удачи!

Источник

Биквадратное уравнение. Алгоритм решения и примеры.

Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.

Формула биквадратного уравнения:

Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.

ax 4 +bx 2 +c=0, где a≠0

Как решаются биквадратные уравнения?

Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
\(x^<2>=t,\;t\geq0\)
t должно быть положительным числом или равным нулю

\(t^<2>-5t+6=0\)
Получилось полное квадратное уравнение, решаем его через дискриминант:
\(D=b^<2>-4ac=(-5)^<2>-4\times1\times6=25-24=1\)
Дискриминант больше нуля, следовательно, два корня, найдем их:

Возвращаемся в замену, подставим вместо переменной t полученные числа: \(x^<2>=3\)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.

Получилось полное квадратное уравнение, решаем через дискриминант:
\(D=b^<2>-4ac=(-4)^<2>-4\times1\times4=16-16=0\)
Дискриминант равен нулю, следовательно, один корень, найдем его:
\(t=\frac<-b><2a>=\frac<-(-4)><2\times1>=2\)

Возвращаемся в замену, подставим вместо переменной t полученное число:

Можно не во всех случаях делать замену. Рассмотрим пример.

Пример №3:
Решить биквадратное уравнение.

Выносим переменную x 2 за скобку,

Приравниваем каждый множитель к нулю

Делим всё уравнение на -4:
Чтобы решить \(x^<2>=4\) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
\(\begin
&x^<2>=4\\
&x_<2>=2\\
&x_<3>=-2\\
\end\)

Пример №4:
Решите биквадратное уравнение.
\(x^<4>-16=0\)

Возвращаемся в замену, подставим вместо переменной t полученное число:
\(\begin
&x^<2>=4\\
&x_<1>=2\\
&x_<2>=-2
\end\)

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Источник

Биквадратные уравнения

теория по математике 📈 уравнения

Уравнение вида ax 4 +bx 2 +c=0, где а≠0 число, называется биквадратным уравнением (приставка «би» означает «двойной»). Для решения такого уравнения применяют метод введения новой переменной, чтобы получить квадратное уравнение, решение которого легко выполняется.

Рассмотрим на примерах решение таких уравнений.

Пример №1. Решить уравнение:

В данном уравнении заменим х 2 на переменную, например а (букву для замены можно брать любую): х 2 =а. Степень данного уравнения при этом понизится на 2, получаем квадратное уравнение:

Решаем данное уравнение, например, по теореме Виета. Тогда:

Методом подбора получаем корни квадратного уравнения 9 и 16. Проверяем, что действительно 9+16=25, 916=144. Теперь переходим к нахождению корней биквадратного уравнения, которое дано по условию. Мы заменяли х 2 на а, поэтому подставляем вместо а полученные значения – это 9 и 16:

Пример №2. Решить уравнение:

Заменим на переменную у: х 2 =у. Получим уравнение:

Найдем его корни: у₁=–1, у₂=4. Подставим корни вместо у и получим уравнения: х 2 =–1; х 2 =4. Видим, что первое неполное квадратное уравнение не имеет корней, а корни второго уравнения – это ±2. Значит, данное биквадратное уравнение имеет корни ±2.

Пример №3. Решить уравнение:

Выполним замену переменной: х 2 =у. Решим уравнение:

Подбором корни найти невозможно, поэтому через дискриминант получаем, что корней нет, так как дискриминант будет отрицательный. Значит и данное биквадратное уравнение тоже не имеет корней.

Источник

Появление методики

Уравнения начали составлять ещё в Древнем Вавилоне. Это было вызвано потребностью находить площади земельных участков, выполнять инженерные работы. Составляли равенства и астрономы, высчитывая расстояния до обнаруживаемых космических тел. Квадратные равенства встречаются в клинописных текстах греков и вавилонян. При этом в этих записях попадаются уравнения, содержащие кубическую или биквадратную степень.

Несмотря на довольно хорошее развитие алгебры в стародавнее время, находимые упоминания о равенствах содержат только ответы, без указаний способов решений. Задачи с примерами решения биквадратных уравнений встречаются у астронома Ариабхатта и индийского учёного Брахмапутра. Формулы для решения сложных уравнений были изложены в сборнике «Книга абака», написанной в 1202 году итальянцем Фибоначчи. Это издание способствовало развитию математики, в частности, алгебре, в Италии, Германии, Франции. Большой вклад в развитие теории решения внесли и советские учёные-математики: Чеботарев, Четаев.

В XVI веках в Китае был разработан способ нахождения корней равенств высшей степени методом Цинь Цзю-шао, после успешно применявшимся в работах Руффини и Горнера.

Этот метод использовал способ подбора, но применим был только для случаев, когда в ответе присутствовали только целые числа.

Все способы решения биквадратных уравнений сводились к приведению их к простому квадратному равенству. Была найдена формула, позволяющая решать уравнения с помощью радикалов (корней). Впервые этот метод предложил Виета, но он был рассчитан только на положительные ответы. Итальянские же учёные Тарталья, Кордано, Бомбелли стали учитывать и отрицательные корни. В итоге Декарт, Жирар и Ньютон привели способы решения к современному виду.

Биквадратные выражения стали разделять на полные и неполные. В алгоритмическом языке корнями уравнения начали называть такие значения неизвестной составляющей, при которой решаемое выражение обращается в правильное числовое равенство. То есть чтобы решить задачу, нужно найти всевозможные его корни или доказать, что решения быть не может.

Основные понятия

Биквадратным уравнением будет называться равенство вида: a*p 4 + b*p 2 + c = 0. Переменные a, b, c могут быть различными числами, при этом A не должно равняться нулю. Символ C называют свободным членом. За P принимают неизвестную переменную, требующую вычисления. Решение уравнений сводится к поиску чисел, которые при подстановке вместо P сделают равенство верным.

Так как значения с1, с2… Cm — это все возможные корни f, то для любого поля будет верным: f (p) = (c — c1) * (c — c2)…(c — cm) * s (p). Учитывая, что s (p) не равно нулю, а f (p) = 0 только в том случае, если C равно некоторому числу I, величина корней многочлена f не может быть более значения m.

Таким образом, уравнение может иметь четыре, три, два, или одно решение. При этом есть вероятность, что ответа может совсем и не быть. Принцип, по которому решаются биквадратные уравнения, следующий:

Квадратные уравнения можно решать любым удобным способом. Типичная схема состоит всего из четырёх шагов и редко вызывает трудности понимания. Пожалуй, сложности могут возникнуть только при нахождении комплексных корней.

Решение равенств

Без знания методов нахождения корней в квадратных уравнениях решить самостоятельно биквадратное равенство не удастся, так как исходное неравенство в итоге приводится к виду квадратичного. Существует несколько способов, позволяющих быстро найти нужные корни или доказать невозможность существования равенства.

К основным относят:

Разложение многочлена на множители основано на группировании и нахождении дискриминанта, то есть знака, по виду которого можно судить о существовании корней. Для решения используется формула: a * p 2 + b * p + c = a * (p — p 1) * (p — p 2), где p и являются корнями уравнения. Этот способ понятен и используется при обучении учащихся решению задач такого типа.

Существуют специальные формулы нахождения корней квадратного, а значит, и биквадратного уравнения. Выглядят они следующим образом: p 1 = (- b — (b 2 — 4 ac) ½ ) / (2* a) и p 2 = (- b + (b 2 + 4 ac) ½ ) / (2* a). С их помощью можно решить любое уравнение. При этом часто для упрощения решения вводят замену подкоренному выражению (b 2 — 4 ac) обозначая его буквой D — дискриминант. Если D больше нуля, то есть два корня, если меньше — решений нет. Если же D = 0, то существует только один корень.

Примеры уравнений

Разложение на множители

Самостоятельная работа, дающаяся в школе, часто предполагает решение биквадратных равенств методом разложения на множители. Связанно это с тем, что этот способ позволяет понять принцип нахождения корней для многочлена любой степени.

Пошагово описать разложение многочлена можно на следующем примере: p 4 + 2p 3 + 3p 2 + 4p +2. Решают его в следующей последовательности:

Вычисление корней требует внимательности и усердия. Для проверки своих навыков можно использовать онлайн-калькуляторы. Это сервисы, использующие специальное программное обеспечение, часто написанное на Паскале, умеют быстро и безошибочно рассчитывать корни любого примера.

Чтобы решить биквадратное уравнение онлайн, особых умений или знаний правил не нужно. Всё, что требуется — это ввести в предложенную форму параметры решаемого равенства. Из наиболее популярных интернет-порталов выделяют Allcalc. Используя его, можно проверить свои знания, исправить допущенные ошибки при самостоятельном расчёте. Причём свои услуги сайт предлагает совершенно бесплатно.

Источник

Биквадратное уравнение

Термин Биквадратное уравнение может означать:

где — заданные комплексные числа и . Подстановкой сводится к квадратному уравнению относительно . Такой переход от одной неизвестной величины к другой называется методом замены неизвестных.

Четыре его корня:

Ссылки

Список значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью.

Полезное

Смотреть что такое «Биквадратное уравнение» в других словарях:

БИКВАДРАТНОЕ УРАВНЕНИЕ — в котором неизвестный член в четвертой степени. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. БИКВАДРАТНОЕ УРАВНЕНИЕ от лат. bis, дважды, и quadratum, квадрат. Уравнение, в котором наибольшая степень… … Словарь иностранных слов русского языка

БИКВАДРАТНОЕ УРАВНЕНИЕ — (от би. и лат. quadratus квадратный) алгебраическое уравнение вида ax4 + bx2 + c = 0. Его решение приводится к решению квадратного уравнения подстановкой y = x2 … Большой Энциклопедический словарь

биквадратное уравнение — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN biquadratic equationfourth power equation … Справочник технического переводчика

биквадратное уравнение — (от би. и лат. quadratus квадратный), алгебраическое уравнение вида ax4 + bx2 + с = 0. Его решение приводится к решению квадратного уравнения подстановкой y = х2. * * * БИКВАДРАТНОЕ УРАВНЕНИЕ БИКВАДРАТНОЕ УРАВНЕНИЕ (от лат. bi дву(х) и… … Энциклопедический словарь

БИКВАДРАТНОЕ УРАВНЕНИЕ — уравнение вида где а, b, с заданные комплексные числа, причем Подстановкой сводится к квадратному уравнению … Математическая энциклопедия

Биквадратное уравнение — (от Би. и лат. quadratus квадратный) уравнение вида ах4 + bx2 +с = 0. Подстановкой х2 = у решение Б. у. приводится к решению квадратного уравнения (См. Квадратное уравнение) … Большая советская энциклопедия

БИКВАДРАТНОЕ УРАВНЕНИЕ — (от 6и. и лат. quadratus квадратный), алгебр. ур ние вида ax4+ax2+с=0. Его решение приводится к решению квадратного ур ния подстановкой у =x2 … Естествознание. Энциклопедический словарь

биквадратное уравнение — матем. Частный случай уравнения четвёртой степени, в котором отсутствуют нечётные степени … Словарь многих выражений

биквадратное уравнение (мат.) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN biquadratic equation … Справочник технического переводчика

Источник