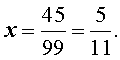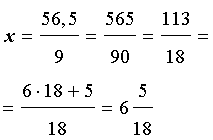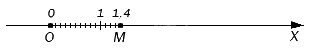Что такое бесконечные десятичные непериодические дроби
Бесконечные периодические и непериодические десятичные дроби
Содержание
Бесконечные периодические и непериодические десятичные дроби
В десятичной записи конечной десятичной дроби после запятой стоит конечное число десятичных знаков.
В десятичной записи бесконечной десятичной дроби после запятой стоит бесконечное число десятичных знаков.
Бесконечные десятичные дроби бывают периодическими и непериодическими.
Повторяющаяся группа цифр называется периодом бесконечной периодической десятичной дроби.
Для обозначения периода десятичной дроби используют круглые скобки.
Бесконечная десятичная дробь, не являющаяся периодической, называется непериодической.
Алгоритм обращения бесконечной периодической десятичной дроби в простую дробь
Разберем алгоритм обращения бесконечной периодической десятичной дроби в простую дробь на примере решений следующих задач.
ОТВЕТ : 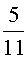
ОТВЕТ : 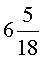
Демонстрационные варианты ЕГЭ и ОГЭ
С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Наши учебные пособия для школьников
При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.
Десятичные дроби, определения, запись, примеры, действия с десятичными дробями.
Эта статья про десятичные дроби. Здесь мы разберемся с десятичной записью дробных чисел, введем понятие десятичной дроби и приведем примеры десятичных дробей. Дальше поговорим о разрядах десятичных дробей, дадим названия разрядов. После этого остановимся на бесконечных десятичных дробях, скажем о периодических и непериодических дробях. Дальше перечислим основные действия с десятичными дробями. В заключение установим положение десятичных дробей на координатном луче.
Навигация по странице.
Десятичная запись дробного числа
Дробные числа, так же как и натуральные числа, можно представлять в виде десятичной записи дробного числа.
Десятичные дроби, определение, примеры десятичных дробей
Отталкиваясь от десятичной записи чисел, можно дать определение десятичных дробей.
Десятичные дроби – это дробные числа, представленные в десятичной записи.
Возникает логичный вопрос: «Для чего нужны десятичные дроби»?
Отсюда вытекает следующий вопрос: «Как дробные числа со знаменателями 10, 100, … записываются в виде десятичных дробей»?
Чтение десятичных дробей
Скажем пару слов о правилах чтения десятичных дробей.
Десятичные дроби, которым соответствуют правильные обыкновенные дроби, читаются также как и эти обыкновенные дроби, только еще предварительно добавляется «ноль целых». Например, десятичной дроби 0,12 отвечает обыкновенная дробь 12/100 (читается «двенадцать сотых»), поэтому, 0,12 читается как «нуль целых двенадцать сотых».
Десятичные дроби, которым соответствуют смешанные числа, читаются абсолютно также как эти смешанные числа. Например, десятичной дроби 56,002 соответствует смешанное число 
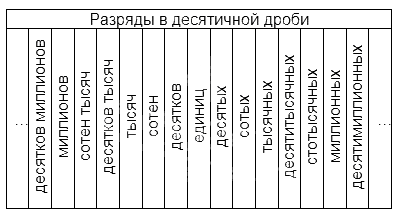
Разряды в десятичных дробях
В записи десятичных дробей, также как и в записи натуральных чисел, значение каждой цифры зависит от ее позиции. Действительно, цифра 3 в десятичной дроби 0,3 означает три десятых, в десятичной дроби 0,0003 – три десяти тысячных, а в десятичной дроби 30 000,152 – три десятка тысяч. Таким образом, мы можем говорить о разрядах в десятичных дробях, так же как и о разрядах в натуральных числах.
Названия разрядов в десятичной дроби до десятичной запятой полностью совпадают с названиями разрядов в натуральных числах. А названия разрядов в десятичной дроби после запятой видны из следующей таблицы.
Например, в десятичной дроби 37,051 цифра 3 находится в разряде десятков, 7 – в разряде единиц, 0 стоит в разряде десятых, 5 – в разряде сотых, 1 – в разряде тысячных.
Конечные десятичные дроби
До этого момента мы говорили лишь о десятичных дробях, в записи которых после десятичной запятой находится конечное число цифр. Такие дроби называют конечными десятичными дробями.
Конечные десятичные дроби – это десятичные дроби, в записях которых содержится конечное число знаков (цифр).
Бесконечные десятичные дроби: периодические дроби и непериодические дроби
В записи десятичной дроби после запятой можно допустить возможность наличия бесконечного количества цифр. В этом случае мы придем к рассмотрению так называемых бесконечных десятичных дробей.
Бесконечные десятичные дроби – это десятичные дроби, в записи которых находится бесконечное множество цифр.
Периодические десятичные дроби (или просто периодические дроби) – это бесконечные десятичные дроби, в записи которых, начиная с некоторого знака после запятой, бесконечно повторяется какая-нибудь цифра или группа цифр, которую называют периодом дроби.
Бесконечные десятичные периодические дроби представляют рациональные числа. Иными словами, любую периодическую дробь можно перевести в обыкновенную дробь, а любую обыкновенную дробь можно представить в виде периодической дроби (смотрите перевод обыкновенной дроби в десятичную дробь и обратно).
Наконец, повнимательнее рассмотрим бесконечные десятичные дроби, в записи которых отсутствует бесконечно повторяющаяся последовательность цифр. Их называют непериодическими.
Непериодические десятичные дроби (или просто непериодические дроби) – это бесконечные десятичные дроби, не имеющие периода.
Отметим, что непериодические дроби не переводятся в обыкновенные дроби, бесконечные непериодические десятичные дроби представляют иррациональные числа.
Действия с десятичными дробями
Одним из действий с десятичными дробями является сравнение, также определены четыре основных арифметических действия с десятичными дробями: сложение, вычитание, умножение и деление. Рассмотрим отдельно каждое из действий с десятичными дробями.
Сравнение десятичных дробей по сути базируется на сравнении обыкновенных дробей, отвечающих сравниваемым десятичным дробям. Однако перевод десятичных дробей в обыкновенные является достаточно трудоемким действием, да и бесконечные непериодические дроби не могут быть представлены в виде обыкновенной дроби, поэтому удобно использовать поразрядное сравнение десятичных дробей. Поразрядное сравнение десятичных дробей аналогично сравнению натуральных чисел. Для получения более детальной информации рекомендуем изучить материал статьи сравнение десятичных дробей, правила, примеры, решения.
Рассмотрим следующее действие с десятичными дробями – сложение десятичных дробей. Наиболее удобно сложение конечных десятичных дробей по правилу, аналогичному сложению столбиком натуральных чисел. Для сложения периодических десятичных дробей приходится их заменять обыкновенными дробями, после чего выполнять сложение обыкновенных дробей. Что касается сложения бесконечных непериодических десятичных дробей, то складываемые дроби обычно предварительно округляют (смотрите округление чисел), придерживаясь требуемой точности, после чего проводят сложение полученных после округления конечных десятичных дробей. Аналогично выполняют и другие действия с бесконечными непериодическими дробями. Далее смотрите статью сложение десятичных дробей, правила, примеры, решения.
Вычитание десятичных дробей представляет собой действие, обратное сложению. То есть, вычитание десятичных дробей – это нахождение числа, которое в сумме с вычитаемой десятичной дробью даст уменьшаемую десятичную дробь. Для дальнейшего изучения этого действия с десятичными дробями подходит статья вычитание десятичных дробей, правила, примеры, решения.
Деление десятичных дробей представляет собой действие, обратное умножению. На практике, деление десятичных дробей сводится к делению десятичной дроби на натуральное число в столбик, которое аналогично делению в столбик натуральных чисел. Дальнейшая информация по теме собрана в статье деление десятичных дробей, правила, примеры, решения.
Десятичные дроби на координатном луче
Между точками координатного луча и десятичными дробями существует взаимно однозначное соответствие.
Разберемся, как строятся точки на координатном луче, соответствующие данной десятичной дроби.
Такой способ построения десятичных чисел на координатном луче позволяет сколь угодно близко приблизиться к точке, отвечающей бесконечной десятичной дроби.
Иногда возможно точно построить точку, соответствующую бесконечной десятичной дроби. Например, 
Обратный процесс получения десятичной дроби, соответствующей данной точке на координатном луче, представляет собой так называемое десятичное измерение отрезка. Разберемся, как оно проводится.
Пусть наша задача заключается в том, чтобы попасть из начала отсчета в данную точку координатной прямой (или бесконечно приблизиться к ней, если попасть в нее не получается). При десятичном измерении отрезка мы можем последовательно откладывать от начала отсчета любое количество единичных отрезков, далее отрезков, длина которых равна десятой доле единичного, затем отрезков, длина которых равна сотой доле единичного, и т.д. Записывая количество отложенных отрезков каждой длины, мы получим десятичную дробь, соответствующую данной точке на координатном луче.
Понятно, что точкам координатного луча, в которые невозможно попасть в процессе десятичного измерения, соответствуют бесконечные десятичные дроби.
Математика. 6 класс
Конспект урока
Непериодические десятичные дроби
Перечень рассматриваемых вопросов:
Рациональное число, можно записать в виде конечной или бесконечной периодической десятичной дроби.
Существуют бесконечные непериодические десятичные дроби. Например, дроби 0,010010001…; 17,12345678910…
Бесконечные десятичные дроби называют числами.
Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.
Рациональные и иррациональные числа называются действительными числами.
Теоретический материал для самостоятельного изучения
Рассмотрим положительную бесконечную десятичную дробь 0,1011011101111…
У этой дроби нет группы цифр, являющейся периодом. Эта дробь непериодическая.
Примеры бесконечных непериодических дробей
Поставив перед положительной дробью знак «–», получим отрицательную дробь.
является отрицательной бесконечной непериодической дробью.
Обнаружены новые числа, которые раньше не встречались. Эти новые для вас числа называют иррациональными.
Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.
Рациональные и иррациональные числа называются действительными числами.
Любое действительное число представляется в виде бесконечной десятичной дроби.
Если число – рациональное, то дробь – периодическая, а если иррациональное, то дробь – непериодическая.
Считается, что иррациональные числа были открыты в Древней Греции приблизительно за 400 лет до нашей эры. Самое знаменитое иррациональное число пи обозначается греческой буквой – π и приближенно равно 3,141592653589793238462643.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют «День числа пи». В этот день даже проводятся соревнования по запоминанию десятичных знаков этого числа.
Что мы знаем о числах?
Рассмотрим, как выполняются действия с действительными числами. На практике бесконечные десятичные дроби складывают, вычитают, умножают и делят приближенно.
Пример 1. Сравните: 0,(23) и 0,1234…
Чтобы сравнить дроби надо уравнять количество десятичных знаков и затем сравнить.
Пример 2. Найдем приближенную сумму и разность чисел а и b, округлив их с точностью до одной десятой, если а = 23,(18), b = – 4,23(75).
Решение: округляя эти числа с точностью до одной десятой, находим, что а ≈ 23,2 и b = – 4,2. Тогда а + b ≈ 19,0; а – b ≈ 27,4.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Тип 2. Единичный выбор
Укажите соседей числа.
Между какими числами расположено иррациональное число 0,1011011…
Десятичные дроби: определения, запись, примеры, действия с десятичными дробями
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Десятичные дроби представляют собой дробные числа в десятичной записи.
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
Что такое разряды в десятичных дробях
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Положение десятичных дробей на оси координат
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
3. Свойства десятичных дробей
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
Деление десятичных дробей друг на друга
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, \( \displaystyle \frac<1><3>,\ \frac<1><4>,\frac<5><112>\).
Наравне с приведенными выше дробями существуют дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
А теперь прочитаем все вместе – «\( 46\) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат \( 10\) на \( 10\) и закрась какую-нибудь его часть равную:
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат \( 10\) на \( 10\) состоит из \( 100\) клеточек. Соответственно, \( 0.05\) – \( 5\) клеточек из \( 100\); \( 0,4\) – \( 40\) клеточек из \( 100\) и так далее.
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
Виды десятичных дробей
Десятичная дробь может быть:
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: \( \displaystyle \frac<1><4>\)? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен \( 10\), \( 100\), \( 1000\) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
Сравним наши ответы:
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
Итак, бери калькулятор и дели \( 1\) на \( 17\). Поделил? Ты получил \( 0,05882352941\) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к \( <<10>^
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как \( \displaystyle \frac<1><17>\).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число \( \pi \) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что \( \pi =3,14\), но это далеко не так. Число \( \pi \) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа \( \pi \). Мировой рекорд по запоминанию знаков числа \( \pi \) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь \( \displaystyle \frac<1><3>\). Что у тебя получилось?
Чтобы не повторять число \( 3\) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
\( \displaystyle \frac<1><3>=0,\underbrace<3>_<период>33333333….=0,\left( 3 \right)\)
\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)
Важно, что период не может начинаться слева от запятой:
\( \displaystyle \frac<100><7>=\underbrace<14,2857>_<не период>1428571428571…=14,\left( 285714 \right)\).