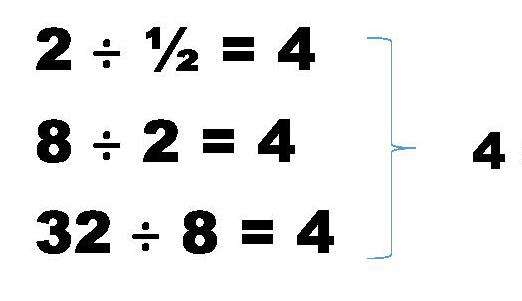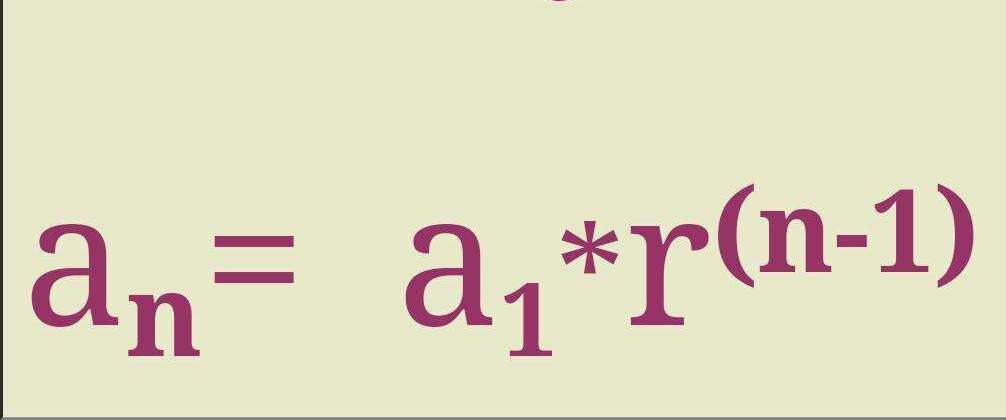Что такое бесконечно убывающая геометрическая прогрессия определение
Бесконечная убывающая геометрическая прогрессия и парадокс Зенона
Когда в общеобразовательных школах изучают свойства упорядоченных последовательностей чисел, то в обязательном порядке рассматривают так называемую убывающую бесконечную геометрическую прогрессию. Раскроем подробнее этот вопрос в статье.
Что такое геометрическая прогрессия?

Исходя из определения этого вида прогрессии, можно n-й ее член найти, используя следующее выражение: an = a1*r(n-1), то есть достаточно знать знаменатель и первый член числового ряда.
Например, найдем 8-е число в геометрической прогрессии, приведенной выше. Имеем: a8 = a1*r7 = 1*47 = 16384.
Еще одной важной формулой для геометрической прогрессии является выражение для нахождения суммы ее n первых членов. Эта формула имеет вид: Sn = a1*(rn-1)/(r-1). Применим ее для нахождения суммы 8-ми чисел из последовательности выше. Получаем: S8 = 1*(48-1)/(4-1) = 21845.
Какие бывают геометрические прогрессии
В зависимости от знака и модуля знаменателя r выделяют 4 вида геометрической прогрессии:
Черепаха и Ахиллес (парадокс Зенона)
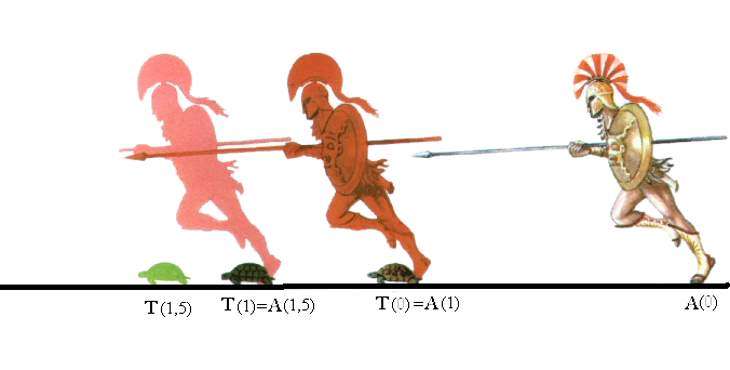
Где можно использовать результат, полученный в пункте выше? Например, при объяснении парадокса древнегреческого философа Зенона. Суть этого парадокса заключается в том, что Ахиллес (с древнегреческого языка это имя переводится, как «тот, кто обладает «легкими» ногами»), будучи самым быстрым воином, не может догнать черепаху.
Зенон рассуждал следующим образом: если черепаха будет впереди Ахиллеса, и они одновременно начнут движение, то когда воин достигнет места, откуда взяла старт черепаха, последняя уже отползет на некоторое расстояние, поэтому Ахиллесу придется снова его преодолевать (хотя оно и меньше, чем первоначальное). Пробежав новый отрезок пути, воин все равно окажется позади черепахи, ведь она опять проползет некоторую дистанцию. Так способом можно рассуждать до бесконечности.
Каждый из нас знает, что не только Ахиллес, но и любой человек, двигаясь пешком, обгонит черепаху. В чем же ошибся философ? Он не учел, что хотя сумма отрезков является бесконечной, она приводит к конечному числу S∞. Как только Ахиллес преодолеет расстояние S∞, он сразу же обгонит черепаху.
Любопытно отметить, что сам философ объяснял тот факт, что Ахиллес на практике все же обгоняет черепаху, тем, что движение и время являются иллюзией, и в реальности не существуют.
Формулы для нахождения суммы бесконечной геометрической прогрессии
Что такое геометрическая прогрессия
Числа \( b_1\) и q не могут равняться нулю, поскольку в таком случае все члены прогрессии, начиная со второго, будут равны нулю.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Геометрическую прогрессию определяют как произведение между ее знаменателем и n-м членом:
Где \(b_n\) — \(n-й\) член прогрессии, \(q\) — знаменатель прогрессии.
Геометрическая прогрессия может быть задана рекуррентным соотношением:
Рекуррентное соотношение задается формулой, выражающей \(Xn\) через предшествующие ему члены последовательности.
Примеры геометрических прогрессий:
Каждый член геометрической прогрессии, начиная со второго, рассчитывается как модуль среднего геометрического соседних членов:
Примеры геометрических прогрессий в жизни:
Бесконечная убывающая геометрическая прогрессия — что из себя представляет
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы \(|q|
Сумма S всех членов бесконечной убывающей геометрической прогрессии вычисляется как соотношение между первым членом геометрической прогрессии к разности между единицей и знаменателем прогрессии:
Доказательством этой формулы является то, что величина \(q^n\) по модулю становится все меньше и меньше и стремится к нулю, при этом величина n неограниченно возрастает.
Пример такой прогрессии:
Сумма первых n членов геометрической прогрессии
Также для объяснения формулы, введем другое обозначение суммы первых членов прогрессии:
Тогда можно видоизменить формулу нахождения суммы \(S_n\) первых n членов геометрической прогрессии:
Как найти q в геометрической прогрессии
Вычисление знаменателя прогрессии \(q\) осуществляют через выведение из формулы на нахождение общего члена геометрической прогрессии:
Примеры решения задач
Сумма первого и третьего членов геометрической прогрессии равна 35. Сумма первых 5 членов в 49 раз больше суммы их обратных величин.
Найти знаменатель и первый член геометрической прогрессии.
По условиям задачи:
Так как \(1+q+q^2+q^3+q^4\neq0\) (иначе задача теряет смысл), то равенство (2) можно записать в виде:
Из (3) следует, что либо \(b_1q^2=7,\) либо \(b_1q^2=-7.\)
\(S_n\) — сумма первых n членов геометрической прогрессии.
Пусть \(b_k — k-й\) член, \(q\) — знаменатель геометрической прогрессии. Тогда:
А из равенств (3) следует равенство (1).
Сумма бесконечно убывающей геометрической прогрессии равна 4. Сумма возведенных в третью степень ее членов равна 192.
Найти первый член и знаменатель этой прогрессии.
Обозначим: \(b_1\) — первый член, \(S\) — сумма прогрессии, \(q\) — знаменатель, \(S_1\) — сумма возведенных в третью степень ее членов.
\(3(1+q+q^2)=1-2q+q^2,\;q\neq1..\)
Полученное уравнение, записанное в виде
имеет корни \(q_1 = −2,\) \(q_2 = − ½.\)
\(S_n\) первых трех членов геометрической прогрессии равна 351. \(S_n\) следующих трех членов равна 13.
Найти первый член и знаменатель прогрессии.
Запишем условия задачи в виде системы уравнений:
\(\left\<\begin
Геометрическая прогрессия содержит четное число членов. Их сумма в три раза больше суммы членов, стоящих на нечетных местах.
Найти знаменатель прогрессии?
Определим, что в прогрессии 2n членов и \(S_<2n>\) — сумма всех членов, а \(S_n^\ast\) — сумма членов, стоящих на нечетных местах.
Где \(b_1\) — первый член прогрессии, а \(q ≠ 1\) — знаменатель прогрессии.
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация

Связь
Содержание
Геометрическая прогрессия
Cумма геометрической прогрессии со знаменателем q, b=1 :
$$S=1 + q +q^2+\cdots=1+q(1+q+\cdots) = 1+q\cdot S$$
Эта же техника может быть использована при вычислении любых самоподобных выражений.
Периодические дроби
Обращение бесконечных периодических дробей в обыкновенные дроби:
$0,(7) = 0,7+0,07+0,007+\ldots = 0,7 / (1-0.1) = 7/10 / (9/10) = 7/9$
Геометрическая интерпретация
Сходимость геометрической прогрессии при q=1/2, b=1/2:
Шутка
Легенда о шахматной доске
Шахматы – одна из самых древних игр. Она существует уже многие века, и неудивительно, что с нею связаны различные предания, правдивость которых, за давностью времени, невозможно проверить.
Об одной из подобных легенд и математической составляющей ее содержания мы сегодня и поведём речь. Чтобы понять ее, не нужно вовсе уметь играть в шахматы: достаточно знать, что игра происходит на доске, разграфленной на 64 клетки.
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
– Я достаточно богат, чтобы исполнить самое смелое твое пожелание, – сказал царь.– Назови награду, которая тебя удовлетворит, и ты получишь ее.
он удивил царя беспримерной скромностью своей просьбы.
– Повелитель, – сказал Сета,– прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
– Простое пшеничное зерно? – изумился царь.
– Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвертую – 8, за пятую – 16, за шестую – 32…
–Довольно, – с раздражением прервал его царь.– Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моею милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.
– Повелитель, – был ответ, – приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
– Повелитель, – ответили ему,– математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.
– Почему медлят с этим делом? – гневно воскликнул царь. – Завтра, прежде чем я проснусь, все до последнего зерна должно быть выдано Сете. Я дважды не приказываю.
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.
– Прежде чем скажешь о твоем деле, – объявил Шерам,– я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
– Ради этого я и осмелился явиться перед тобой в столь ранний час,– ответил старик.– Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…
– Как бы велико оно ни было, – надменно перебил царь, житницы мои не оскудеют. Награда обещана и должна быть выдана…
– Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду. С изумлением внимал царь словам старца.
– Назови же мне это чудовищное число, – сказал он в раздумье.
– Восемнадцать квинтиллионов четыреста сорок шесть квадриллионов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!
S = 18 446 744 073 709 551 615.
Это количество зерна примерно в 1800 раз превышает мировой урожай пшеницы за год (в 2008 – 2009 аграрном году урожай составил 686 млн тонн), то есть превышает весь урожай пшеницы, собранный за всю историю человечества.
Индусский царь не в состоянии был выдать подобной награды. Но он легко мог бы, будь он силен в математике, освободиться от столь обременительного долга. Для этого нужно было лишь предложить Сете самому отсчитать себе зерно за зерном всю причитавшуюся ему пшеницу.
В самом деле: если бы Сета, принявшись за счет, вел его непрерывно день и ночь, отсчитывая по зерну в секунду, он в первые сутки отсчитал бы всего 86 400 зерен. Чтобы отсчитать миллион зерен, понадобилось бы не менее 10 суток неустанного счета. Один кубический метр пшеницы он отсчитал бы примерно за полгода. И осталось бы отсчитать ещё 1 499 999 999 999 м3. Вы видите, что, посвятив счету даже весь остаток своей жизни, Сета получил бы лишь ничтожную часть потребованной им награды.
Экспоненциальный рост
Стремительное возрастание значений величины, подобное тому, которое мы наблюдали, в математике называется экспоненциальным ростом.
Экспоненциальный рост – возрастание величины, когда скорость роста пропорциональна значению самой величины. Говорят, что такой рост подчиняется экспоненциальному закону. В случае дискретной области определения с равными интервалами его еще называют геометрическим ростом (значения функции образуют геометрическую прогрессию).
Для любой экспоненциально растущей величины чем большее значение она принимает, тем быстрее растет. Также это означает, что величина зависимой переменной и скорость ее роста прямо пропорциональны.
Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов.
Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейной или степенной зависимостям.
Сумма бесконечной геометрической прогрессии
Геометрическая прогрессия бывает убывающей, если знаменатель по модулю меньше единицы.
Убывающую геометрическую прогрессию можно видеть, например, в апориях Зенона «Деление пополам» и «Ахиллес и черепаха». В первом случае наглядно показывается, что вся дорога (предположим, длины 1) является суммой бесконечного числа отрезков 1/2, 1/4, 1/8 и т. д. Так оно, конечно, и есть с точки зрения представлений о конечной сумме бесконечной геометрической прогрессии. И все же – как такое может быть?
Прогрессия с коэффициентом 1/2
Предел складывания бумаги
Предел складывания бумаги пополам — физический феномен, суть которого состоит в том, что лист обычной бумаги размера А4 можно сложить пополам не более 7 раз. Он происходит из-за быстроты роста показательной функции.
Если бумагу сложили пополам пять раз, то количество слоёв будет два в степени пять, то есть тридцать два.
Если бумагу сложили пополам 7 раз, то количество слоёв будет два в степени 7, то есть 128.
Уже в Древнем Египте знали не только арифметическую, но и геометрическую прогрессию. Вот, например, задача из папируса Райнда: «У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»
Людей всего 7, кошек 72 = 49, они съедают всего 73 = 343 мыши, которые съедают всего 74 = 2401 колосьев, из них вырастает 75 = 16807 мер ячменя, в сумме эти числа дают 19 607.
Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.