Что такое базисная строка и столбец

Лекция 6. Раздел 6.3
Базисный минор и ранг матрицы.

Введя понятие линейной комбинации строк и столбцов матрицы, как это было сделано у векторов, можно ввести понятие их линейной зависимости и независимости.

Определение 6.3.1. Строки , . называются линейно зависимыми, если существуют такие числа , не все равные нулю, что справедливо равенство .

Здесь 0 – нулевая строка.

Определение 6.3.2. Строки называются линейно независимыми, если их линейная комбинация обращается в ноль лишь при условии, что .

В этом случае линейная комбинация называется тривиальной.

Так же как и у векторов имеется соответствующая теорема.

Теорема 6.3.1. Для того чтобы строки были линейно зависимы, необходимо и достаточно, чтобы одна из них была линейной комбинацией остальных.

Доказательство проводится так же, как и в п. 1.4.

Теорема 6.3.2. Если в систему строк матрицы входит нулевая строка, то эти строки линейно зависимы.

Доказательство. Действительно, нулевая строка представляет собой тривиальную линейную комбинацию любых строк. Но тогда мы сразу переходим к теореме 1.

Рассмотрим теперь понятие базисного минора. Пусть имеется произвольная матрица порядка :

.

Определение 6.3.3. Минором -го порядка матрицы называется определитель -го порядка с элементами, лежащими на пересечении любых строк и столбцов матрицы .

Определение 6.3.4. В матрице , порядка , минор порядка называется базисным, если он не равен нулю, а все остальные миноры порядка равны нулю или миноров порядка вообще нет, то есть совпадает с меньшим из чисел или .

Очевидно, что в матрице может быть несколько базисных миноров, но все они должны быть одного порядка.

Определение 6.3.5. Рангом матрицы называется порядок базисного минора.

Обозначается ранг матрицы – . Строки и столбцы, на пересечении которых стоят элементы базисного минора, называются базисными.

Теорема 6.3.3. (Теорема о базисном миноре). Базисные строки и столбцы линейно независимы. Любая другая строка или столбец матрицы являются линейной комбинацией базисных строк или столбцов.

Доказательство проведем для строк. Покажем вначале, что базисные строки линейно независимы. Если бы они были линейно зависимы, то одна из этих строк была бы линейной комбинацией остальных. Тогда на основании свойств определителя эту комбинацию можно вычесть из указанной строки и получить на ее месте ноли. Но если вся строка состоит из нолей, то минор равен нулю, что противоречит теореме.

Докажем вторую часть этой теоремы. Рассмотрим любой минор -го порядка, включающий в себя базисный. Расположим базисный минор в левом верхнем углу:

.

По определению данный минор равен нулю. Раскроем его по последнему столбцу:

.

Здесь , разделим на него все равенство:

Из полученного выражения следует, что -ая строка является линейной комбинацией базисных строк.

Отсюда можно сделать вывод, что число линейно независимых строк или столбцов равно рангу матрицы. Это свойство используется для практического вычисления .

Источник

Ранг матрицы и базисный минор матрицы

Пример 3.4. Записать миноры разных порядков матрицы

Пример 3.5. Найти все базисные миноры и ранг матрицы

Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих определителей третья строка нулевая. Поэтому базисным может быть только минор второго порядка, расположенный в первых двух строках матрицы. Перебирая 6 возможных миноров, отбираем отличные от нуля

Каждый из этих пяти миноров является базисным. Следовательно, ранг матрицы равен 2.

1. Если в матрице все миноры k-го порядка равны нулю, то равны нулю и миноры более высокого порядка. Действительно, раскладывая минор (k+1)-ro порядка по любой строке, получаем сумму произведений элементов этой строки на миноры k-го порядка, а они равны нулю.

2. Ранг матрицы равен наибольшему порядку отличного от нуля минора этой матрицы.

3. Если квадратная матрица невырожденная, то ее ранг равен ее порядку. Если квадратная матрица вырожденная, то ее ранг меньше ее порядка.

Теоремы о базисном миноре и о ранге матрицы

Рассмотрим основные теоремы, выражающие свойства линейной зависимости и линейной независимости столбцов (строк) матрицы.

Действительно, без ограничения общности предполагаем, что в матрице размеров базисный минор расположен в первых строках и первых столбцах. Рассмотрим определитель

Теорема о базисном миноре служит для доказательства следующих важных теорем.

Условие равенства нулю определителя

Теорема 3.2 (необходимое и достаточное условие равенства нулю определителя). Для того чтобы определитель был равен нулю необходимо и достаточно, чтобы один из его столбцов <одна из его строк) был линейной комбинацией остальных столбцов (строк).

Инвариантность ранга матрицы при элементарных преобразованиях

Теорема 3.3 (об инвариантности ранга при элементарных преобразованиях). При элементарных преобразованиях столбцов (строк) матрицы ее ранг не меняется.

Следствие 1. Если одна строка (столбец) матрицы является линейной комбинацией других ее строк (столбцов), то эту строку (столбец) можно вычеркнуть из матрицы, не изменив при этом ее ранга.

Действительно, такую строку при помощи элементарных преобразований можно сделать нулевой, а нулевая строка не может входить в базисный минор.

Следствие 2. Если матрица приведена к простейшему виду (1.7), то

Действительно, матрица простейшего вида (1.7) имеет базисный минор r-го порядка.

Следствие 3. Любая невырожденная квадратная матрица является элементарной, другими словами, любая невырожденная квадратная матрица эквивалентна единичной матрице того же порядка.

Теорема 3.4 (о ранге матрицы). Ранг матрицы равен максимальному числу линейно независимых строк этой матрицы.

Следствие 1. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов:

Это утверждение вытекает из теоремы 3.4, если ее применить к строкам транспонированной матрицы и учесть, что при транспонировании миноры не изменяются (свойство 1 определителя).

Следствие 2. При элементарных преобразованиях строк матрицы линейная зависимость (или линейная независимость) любой системы столбцов этой матрицы сохраняется.

1. В силу следствия 1 теоремы 3.4 свойство столбцов, указанное в следствии 2, справедливо и для любой системы строк матрицы, если элементарные преобразования выполняются только над ее столбцами.

2. Следствие 3 теоремы 3.3 можно уточнить следующим образом: любую невырожденную квадратную матрицу, используя элементарные преобразования только ее строк (либо только ее столбцов), можно привести к единичной матрице того же порядка.

Ранге произведения и суммы матриц

Теорема 3.5 (о ранге произведения матриц). Ранг произведения матриц не превышает ранга множителей:

Теорема 3.6 о ранге суммы матриц. Ранг суммы матриц не превышает суммы рангов слагаемых:

Источник

Что такое базисная строка и столбец

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Теорема о базисном миноре матрицы Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

§ 3. Теорема о базисном миноре матрицы

Указанные n равенств (1.42) удобно записать в виде одного равенства

Всякий раз, когда будет встречаться равенство (1.43), мы будем понимать его в смысле n равенств (1.42).
Введем теперь понятие линейной зависимости строк.
Определение. Строки A=(a₁,a₂. a_n), В = (b₁, b₂. b_n). С = (с₁, с₂. с_n) назовем линейно зависимыми, если найдутся такие числа α, β. γ не все равные нулю, что справедливы равенства

Указанные n равенств (1.44) удобно записать в виде одного равенства

а это и означает, что строка А является линейной комбинацией строк В. С.
2) Достаточность. Пусть одна из строк (например, А) является линейной комбинацией остальных строк. Тогда найдутся числа

Минором k-го порядка матрицы А будем называть определитель k- г о порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов матрицы А. (Конечно, k не превосходит наименьшее из чисел т и п.)
Предположим, что хотя бы один из элементов а_ij матрицы А отличен от нуля. Тогда найдется такое целое положительное число r, что будут выполнены следующие два условия: 1) у матрицы А имеется минор r-го порядка, отличный от нуля, 2) всякий минор

(г + 1)-го и более высокого порядка (если таковые существуют) равен нулю.
Число г, удовлетворяющее требованиям 1) и 2), назовем рангом матрицы А ( р анг матрицы А, все элементы которой — нули, по определению равен нулю). Тот минор r-го порядка, который отличен от нуля, назовем базисным минором (конечно, у матрицы А может быть несколько миноров r-го порядка, отличных от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами.
Докажем следующую основную теорему.
Теорема 1.6 (теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов).
Доказательство. Все рассуждения проведем для строк.
Если бы базисные строки были линейно зависимы, то по теореме 1.5 одна из этих строк являлась бы линейной комбинацией других базисных строк, и мы могли бы, не изменяя величины базисного минора, вычесть из этой строки указанную линейную комбинацию и получить строку, целиком состоящую из нулей, а это противоречило бы тому, что базисный минор отличен от нуля. Итак, базисные строки линейно независимы.
Докажем теперь, что любая строка матрицы А является линейной комбинацией базисных строк. Так как при произвольных переменах строк (или столбцов) определитель сохраняет свойство равенства нулю, то мы, не ограничивая общности, можем считать, что базисный минор находится в левом верхнем углу матрицы (1.47), т.е. расположен на первых г строках и первых г столбцах. Пусть j — любое число от 1 до n, а k — любое число от 1 до m.
Убедимся в том, что определитель (г + 1)-го порядка

(для всех j = 1, 2. n). Учитывая, что в последних равенствах алгебраическое дополнение c_r+1 = A_kj совпадает с заведомо отличным от нуля базисным минором, мы можем поделить каждое из этих равенств на c_r+1. Но тогда, вводя обозначения

Источник

Теорема о базисном миноре матрицы

В данной публикации мы рассмотрим теорему о базисном миноре (формулировка и следствия). Также разберем пример задачи для демонстрации ее применения на практике.

Формулировка теоремы

В произвольной матрице A столбцы/строки, входящие в состав базисного минора M (называются “базисными”), линейно независимы. Каждый столбец/строка матрицы является линейной комбинацией базисных столбцов/строк.

Из теорему о базисном миноре следует:

Пример задачи

Давайте найдем всем базисные миноры матрицы A, представленной ниже, а также определим ее ранг.

Решение:

1. Выполним элементарные преобразования над матрицей, чтобы упростить ее. Для начала разделим третью строку на 2 и переставим ее с первой местами.

2. Отнимем из третьей строки первую.

3. Получаем матрицу с нулевой строкой, что означает, что все миноры третьего порядка равняются нулю.

4. Таким образом, базисными в нашем случае могут быть только ненулевые миноры второго порядка, состоящие из первой и второй строк полученной матрицы.

Источник

Ранг матрицы. Базисные строки

Определение. Рангом матрицы называется максимальное число линейно независимых строк этой матрицы.

Определение. Говорят, что базисными строками матрицы можно объявить те ее строки, которые являются линейно независимыми, а их число равно рангу матрицы.

Выбор базисных строк, вообще говоря, неоднозначен.

Теорема. Ранг матрицы не меняется при элементарных преобразованиях строк.

Доказательство.Проведем доказательство индукцией по числу примененных элементарных преобразований. Пусть применено одно элементарное преобразование.

Если это элементарное преобразование первого типа, то новая матрица содержит те же строки, что и старая, только в другом порядке. Соответственно, линейно независимыми остались в точности те наборы строк, которые были таковыми.

Если применено элементарное преобразование второго типа, то строки старой матрицы перешли в строки новой матрицы. Сначала покажем, что при переходе от старой матрице к новой ранг не мог увеличиться. Пусть ранг старой матрицы равен , т. е. старая матрица имеет линейно независимых строк, но любые ее строк линейно зависимы. Предположим противное: в новой матрице имеется линейно независимых строк. Поскольку, при переходе от старой матрицы к новой изменениям подверглась только i-я строка, то линейно независимых строк содержат i-ю строку и без i-й строки оставшиеся строк линейно независимы. Таким образом, пусть – линейно независимые строки. По определению линейной независимости только в тривиальном случае. Т. е. только при . Но тогда, если строка содержится среди строк старой матрицы, то строка, а если строка не содержится среди строк старой матрицы, то строки старой матрицы являются линейно независимыми. Полученное противоречие показывает, что ранг новой матрицы не больше ранга старой. Заметим, что от новой матрицы можно вернуться к старой, прибавляя к i-й строке j-ю строку , умноженную на . Следовательно, аналогично доказывается, что ранг старой матрицы не больше ранга новой.

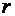
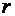
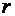
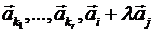
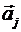
Если применено элементарное преобразование третьего типа, то строки старой матрицы перешли в строки новой матрицы, где . Очевидно, что изменения коснулись только таких линейных комбинаций строк, в которых есть i-я строка. Т. е. линейной комбинации строк старой матрицы соответствует линейная комбинация строк новой матрицы. Эти линейные комбинации будут равны, если , причем из равенства следует, что в точности тогда, когда . Поэтому, если существует нетривиальный набор , такой что , то существует нетривиальный набор , такой что , и наоборот. Следовательно, элементарное преобразование третьего типа сохраняет отношение линейной зависимости (или независимости) на наборах соответствующих строк старой и новой матриц, а значит, не меняется ранг.

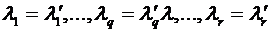
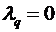
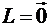
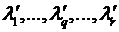
Доказав теорему для случая одного элементарного преобразования, в предположении, что мы можем доказать ее для случая (t–1)-го элементарного преобразования, докажем для случая t элементарных преобразований ( ). Пусть А – начальная матрица, В – конечная, а С – матрица, возникшая после применения к А первого из элементарных преобразований. Тогда на основании доказанного ранги матриц А и С равны, а на основании индуктивного предположения ранги С и В равны. Следовательно, ранги А и В равны.■

Используя эту теорему можно находить ранг матрицы как число ненулевых строк в ее ступенчатом виде (т. е. в ступенчатой матрице, полученной из данной с помощью элементарных преобразований строк). Аналогично базисными строками можно объявить те строки изначальной матрицы, которые при приведении к ступенчатому виду перешли в ненулевые.

Определители

Дадим индуктивное определение определителя (разложением по первой строке).

Определение. Определителем (n-го порядка) назовем отображение, которое определено на множестве квадратных матриц (размерности n×n), принимает значения на множестве действительных чисел и организовано следующим образом:

· при квадратной матрице первого порядка ставится в соответствие то число, которое содержится в ее клетке, т. е. , где – обозначение для определителя;

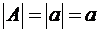
· предполагая определенными определители порядка n, где , определитель порядка k введем соотношением

.

Помимо обозначения также используются обозначения и .

Теорема. Определители можно вычислять разложением по любому столбцу или по любой строке, при этом имеют место равенства:

,

где ( ) называется минором ( )-го порядка, соответствующим элементу ( ) и является определителем матрицы, полученной из матрицы А вычеркиванием i—й (k—й) строки и k—го (j—го) столбца.

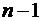
Доказательство. Если по определению определителя расписать его миноры ( 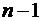)-го порядка до сумм произведений чисел, то можно увидеть, что результат не зависит от того, разложением по какой строке или какому столбцу мы пользовались при сведении вычисления определителя n-го порядка к вычислению этих миноров.■

Теорема. Если матрица А содержит нулевую строку, то определитель .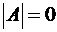

Доказательство. Если разложить определитель по нулевой строке, то очевидно получим 0.■

Теорема. Если от матрицы А к матрице В можно перейти с помощью одного элементарного преобразования строк первого типа, то .

Доказательство. Пусть от матрицы А к матрице В можно перейти с помощью перемены местами i-й и j-й строк. Разложив определители этих матриц по i-й строке, каждый из получившихся миноров ( 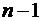)-го порядка разложим по j-й строке. В результате увидим, что полученные разложения будут отличаться только знаками при слагаемых.■

Теорема.Если матрица А содержит две одинаковые строки, то определитель .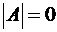

Доказательство.С одной стороны, переставляя местами две одинаковые строки, получим определитель, отличающийся от исходного знаком. С другой стороны, это тот же самый определитель. Очевидно, только число 0 обладает таким свойством.■

Теорема. Если от матрицы А к матрице В можно перейти с помощью одного элементарного преобразования строк второго типа, то .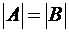

Доказательство.

= ( ) +…+

+ ( ) =

= +…+ +

= ( +…+ )=

= + = = ,

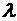
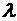
поскольку один из определителей содержит две одинаковых строки.■

Теорема. Если от матрицы А к матрице В можно перейти с помощью одного элементарного преобразования строк третьего типа, где – соответствующий коэффициент, то .

Доказательство.Пусть от матрицы А к матрице В можно перейти с помощью домножения i-й строки на . Разложив определитель матрицы В по i-й строке и вынеся за скобки , в скобках получим разложение по i-й строке определителя матрицы А.■

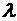
Теорема. Определитель ступенчатой матрицы равен произведению ее элементов, стоящих на главной диагонали.

Доказательство. Раскладывая определитель в соответствии с его определением до сумм произведений его элементов, учитывая определение ступенчатого вида матрицы, убеждаемся, что все слагаемые кроме одного наверняка будут нулями. Оставшееся слагаемое есть произведение элементов главной диагонали.■

Теорема.Определитель матрицы А равен определителю транспонированной матрицы .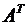

Доказательство. Раскладывая определители матриц А и 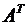в соответствии с определением определителя до сумм произведений элементов этих матриц, получаем выражения, отличающиеся только порядком слагаемых и порядком множителей в слагаемых. Следовательно, .■

Таким образом, все теоремы о свойствах определителя, доказанные для строк, также имеют место и для столбцов.

Теорема.Строки (столбцы) квадратной матрицы линейно независимы тогда и только тогда, когда ее определитель отличен от нуля.

Доказательство. Основываясь на свойствах определителя, заметим, что если от квадратной матрицы А к квадратной матрице В перешли с помощью элементарных преобразований строк, тоопределители этих матриц либо оба нулевые, либо оба ненулевые.

Если строки матрицы А размерности r линейно независимы, то число ненулевых строк в ее ступенчатом виде равно r. Тогда число опорных элементов равно r. Поскольку они стоят в разных строках и столбцах, сдвигаясь с каждой строкой направо, то опорные элементы совпадают с элементами главной диагонали. Следовательно, среди элементов главной диагонали нет нулевых, а значит, определитель ступенчатой матрицы неравен нулю.

Обратно, если определитель ступенчатой матрицы неравен нулю, то среди элементов главной диагонали нет нулевых. Тогда она не имеет нулевых строк. Следовательно, ранг матрицы А равен ее размерности r, т. е. строки матрицы А линейно независимы.

Для столбцов утверждение следует из того, что .■

Теорема.У всякой матрицы А ранга r имеется r линейно независимых столбцов, и любой набор из более чем r столбцов линейно зависим.

Доказательство.Рассмотрим минор М порядка r, составленный из элементов матрицы А, находящихся на пересечении базисных строк, и столбцов, в которых будут стоять опорные элементы, если матрицу А привести к ступенчатому виду с помощью элементарных преобразований строк (таких столбцов будет также r). При приведении матрицы А к ступенчатому виду Гаусса минор М перейдет в минор от единичной матрицы размерности r. Следовательно, . Тогда , а значит, столбцы минора М линейно независимы. Получается, что столбцы матрицы А, содержащие столбцы минора М, тоже линейно независимы.

Если предположить, что имеется r+1 линейно независимый столбец матрицы А, то, взяв минор М порядка r+1, с элементами, принадлежащими этим столбцам и какой-нибудь (r+1)-й строке, получим, что минор М имеет r+1 линейно независимый столбец, т. е. . При приведении матрицы А к ступенчатому виду минор М перейдет в минор . При этом . Следовательно, ступенчатый вид матрицы А имеет по крайней мере (r+1)-у ненулевую строку, что противоречит тому, что ранг матрицы А равен r.■

Определение. Говорят, что базисными столбцами матрицы можно объявить те ее столбцы, которые являются линейно независимыми, а их число равно рангу матрицы.

Определение.Говорят, что базисным минором матрицы можно объявить ее минор, элементы которого располагаются на пересечении строк и столбцов, которые можно объявить базисными.

Выбор базисного минора, вообще говоря, неоднозначен. Базисный минор неравен нулю. Его порядок равен рангу матрицы. Минор матрицы, порядок которого больше порядка базисного минора, равен нулю. Таким образом, ранг матрицы равен не только максимальному числу линейно независимых строк этой матрицы, но и максимальному числу линейно независимых столбцов этой матрицы, и максимальному порядку отличного от нуля минора этой матрицы. Также ранг матрицы А равен рангу матрицы , транспонированной к матрице А.

Источник