Что такое байт килобайт мегабайт гигабайт информатика
Компьютерная грамотность с Надеждой
Заполняем пробелы — расширяем горизонты!
Единицы измерения объема информации
Для измерения длины есть такие единицы, как миллиметр, сантиметр, метр, километр. Известно, что масса измеряется в граммах, килограммах, центнерах и тоннах. Бег времени выражается в секундах, минутах, часах, днях, месяцах, годах, веках. Компьютер работает с информацией и для измерения ее объема также имеются соответствующие единицы измерения.
Бит и байт — минимальные единицы измерения информации
Мы уже знаем, что компьютер воспринимает всю информацию через нули и единички.
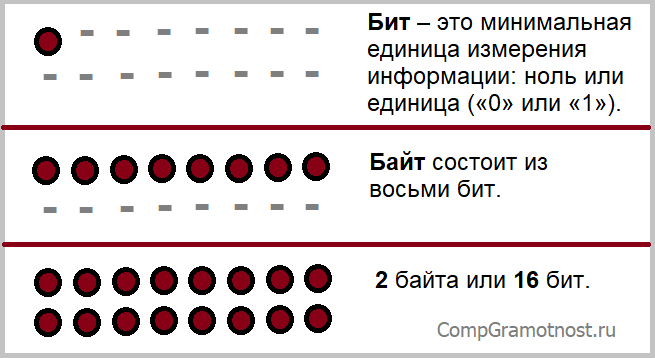
Бит – это минимальная единица измерения информации, соответствующая одной двоичной цифре («0» или «1»).
Бит — это только 0 («ноль») или только 1 («единичка»). С помощью одного бита можно записать одно из двух состояний: 0 (ноль) или 1 (один). Чтобы записать два состояния, потребуется два бита. Бит — это минимальная ячейка памяти, меньше не бывает. В этой ячейке может храниться либо нолик, либо единичка.
Байт состоит из восьми бит. Используя один байт, можно закодировать один символ из 256 возможных (256 = 2 8 ). Таким образом, один байт равен одному символу, то есть 8 битам:
1 символ = 8 битам = 1 байту.
Буква, цифра, знак препинания — это символы. Одна буква — один символ. Одна цифра — тоже один символ. Один знак препинания (либо точка, либо запятая, либо вопросительный знак и т.п.) — снова один символ. Один пробел также является одним символом.
Кроме бита и байта, конечно же, есть и другие, более крупные единицы измерения информации.
Таблица байтов:
1 Кб (1 Килобайт) = 2 10 байт = 2*2*2*2*2*2*2*2*2*2 байт =
= 1024 байт (примерно 1 тысяча байт – 10 3 байт)
1 Мб (1 Мегабайт) = 2 20 байт = 1024 килобайт (примерно 1 миллион байт – 10 6 байт)
1 Гб (1 Гигабайт) = 2 30 байт = 1024 мегабайт (примерно 1 миллиард байт – 10 9 байт)
1 Тб (1 Терабайт) = 2 40 байт = 1024 гигабайт (примерно 10 12 байт). Терабайт иногда называют тонна.
1 Пб (1 Петабайт) = 2 50 байт = 1024 терабайт (примерно 10 15 байт).
1 Эксабайт = 2 60 байт = 1024 петабайт (примерно 10 18 байт).
1 Зеттабайт = 2 70 байт = 1024 эксабайт (примерно 10 21 байт).
1 Йоттабайт = 2 80 байт = 1024 зеттабайт (примерно 10 24 байт).
Такое приближение (или округление) вполне допустимо и является общепринятым.
Ниже приводится таблица байтов с английскими сокращениями (в левой колонке):
10 3 b = 10*10*10 b= 1000 b – килобайт
10 6 b = 10*10*10*10*10*10 b = 1 000 000 b – мегабайт
10 21 b – зеттабайт
10 24 b – йоттабайт
Выше в правой колонке приведены так называемые «десятичные приставки», которые используются не только с байтами, но и в других областях человеческой деятельности. Например, приставка «кило» в слове «килобайт» означает тысячу байт. В случае с километром она соответствует тысяче метров, а в примере с килограммом она равна тысяче грамм.
Продолжение следует…
Возникает вопрос: есть ли продолжение у таблицы байтов? В математике есть понятие бесконечности, которое обозначается как перевернутая восьмерка: ∞.
Напоследок парочка примеров по устройствам, на которые можно записать терабайты и гигабайты информации.
Есть удобный «терабайтник» – внешний жесткий диск, который подключается через порт USB к компьютеру. На него можно записать терабайт информации. Особенно удобно для ноутбуков (где смена жесткого диска бывает проблематична) и для резервного копирования информации. Лучше заранее делать резервные копии информации, а не после того, как все пропало.
CD-диски могут вмещать 650 Мб, 700 Мб, 800 Мб и 900 Мб.
DVD-диски рассчитаны на большее количество информации: 4.7 Гб, 8.5 Гб, 9.4 Гб и 17 Гб.
Упражнения по компьютерной грамотности
Статья закончилась, но можно еще прочитать:
Нашли ошибку? Выделите фрагмент текста и нажмите Ctrl+Enter.
Информатика. 7 класс
Конспект урока
Единицы измерения информации
Перечень вопросов, рассматриваемых в теме:
Каждый символ информационного сообщения несёт фиксированное количество информации.
Единицей измерения количества информации является бит – это наименьшаяединица.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Формулы, которые используются при решении типовых задач:
Информационный объём сообщения определяется по формуле:
I – объём информации в сообщении;
К – количество символов в сообщении;
i – информационный вес одного символа.
Теоретический материал для самостоятельного изучения.
Любое сообщение несёт некоторое количество информации. Как же его измерить?
Одним из способов измерения информации является алфавитный подход, который говорит о том, что каждый символ любого сообщения имеет определённый информационный вес, то есть несёт фиксированное количество информации.
Сегодня на уроке мы узнаем, чему равен информационный вес одного символа и научимся определять информационный объём сообщения.
Что же такое символ в компьютере? Символом в компьютере является любая буква, цифра, знак препинания, специальный символ и прочее, что можно ввести с помощью клавиатуры. Но компьютер не понимает человеческий язык, он каждый символ кодирует. Вся информация в компьютере представляется в виде нулей и единичек. И вот эти нули и единички называются битом.
Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется один бит.
Эту формулу можно применять для вычисления информационного веса одного символа любого произвольного алфавита.
Алфавит древнего племени содержит 16 символов. Определите информационный вес одного символа этого алфавита.
Составим краткую запись условия задачи и решим её:
Информационный вес одного символа этого алфавита составляет 4 бита.
Сообщение состоит из множества символов, каждый из которых имеет свой информационный вес. Поэтому, чтобы вычислить объём информации всего сообщения, нужно количество символов, имеющихся в сообщении, умножить на информационный вес одного символа.
Математически это произведение записывается так: I = К · i.
Например: сообщение, записанное буквами 32-символьного алфавита, содержит 180 символов. Какое количество информации оно несёт?
I = 180 · 5 = 900 бит.
Итак, информационный вес всего сообщения равен 900 бит.
В алфавитном подходе не учитывается содержание самого сообщения. Чтобы вычислить объём содержания в сообщении, нужно знать количество символов в сообщении, информационный вес одного символа и мощность алфавита. То есть, чтобы определить информационный вес сообщения: «сегодня хорошая погода», нужно сосчитать количество символов в этом сообщении и умножить это число на восемь.
I = 23 · 8 = 184 бита.
Значит, сообщение весит 184 бита.
Как и в математике, в информатике тоже есть кратные единицы измерения информации. Так, величина равная восьми битам, называется байтом.
Бит и байт – это мелкие единицы измерения. На практике для измерения информационных объёмов используют более крупные единицы: килобайт, мегабайт, гигабайт и другие.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Итак, сегодня мы узнали, что собой представляет алфавитный подход к измерению информации, выяснили, в каких единицах измеряется информация и научились определять информационный вес одного символа и информационный объём сообщения.
Материал для углубленного изучения темы.
Как текстовая информация выглядит в памяти компьютера.
Набирая текст на клавиатуре, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111. Теперь возникает вопрос, какой именно восьмизначный двоичный код поставить в соответствие каждому символу?
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код ‑ просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для разных типов компьютеров используются различные таблицы кодировки.
Таблица ASCII (или Аски), стала международным стандартом для персональных компьютеров. Она имеет две части.
В этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.
Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:
01100110 01101001 01101100 01100101.
А теперь попробуем решить обратную задачу. Какое слово записано следующим двоичным кодом:
01100100 01101001 01110011 01101011?
В таблице 2 приведен один из вариантов второй половины кодовой таблицы АSСII, который называется альтернативной кодировкой. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования.
Вывод: все тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные для нас буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.
Из памяти же компьютера текст может быть выведен на экран или на печать в символьной форме.
Сейчас используют целых пять систем кодировок русского алфавита (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид. Поэтому, всегда нужно уточнять, какая система кодирования установлена на компьютере.
Разбор решения заданий тренировочного модуля
№1. Определите информационный вес символа в сообщении, если мощность алфавита равна 32?
№2. Выразите в килобайтах 2 16 байтов.
2 6 = 64, а 2 10 байт – это 1 Кб. Значит, 64 · 1 = 64 Кб.
№3. Тип задания: выделение цветом
8 х = 32 Кб, найдите х.
Что такое байт (килобайт, мегабайт, гигабайт, терабайт) и бит, а также особенности единиц измерения количества информации
Здравствуйте, уважаемые читатели блога Goldbusinessnet.com. В ходе развития современных компьютерных и интернет-технологий наиважнейшее значение приобретают единицы измерения, необходимые при хранении и передаче информации, коими являются бит и байт.
Все данные хранятся или передаются в закодированном цифровом формате, потому возможность измерить их объем позволяет обеспечить системность и устойчивость в работе с ними.
По аналогии с известными физическими единицами измерения, которые при большой их величине для удобства исчисления получают увеличительные приставки (1000 метров = 1 километр, 1000 грамм = 1 килограмм), байт тоже имеет свои производные (килобайт, мегабайт, гигабайт и т.д.).
Однако, в случае бита и байта существуют свои особенности, связанные с цифровой сущностью системы, которые ниже будут подробно разъяснены. Кроме того, будут рассмотрены соотношение между байтом и битом, суть понятия «машинное слово» и другие нюансы.
Единицы измерения информации бит (bit) и байт (byte)
Чтобы стало понятнее, придется изложить все поподробнее и начать, так сказать, с истоков. Однако, постараюсь донести информацию без заумных математических формул и терминов. Начнем с того, что существует несколько позиционных систем счисления. Все их перечислять нет необходимости, но для ясности остановимся на двух основных.
Десятичная и двоичная системы счисления
Самая известная из них, с которой мы все сталкиваемся ежедневно, это десятичная система. В ней любое число состоит из цифр (от 0 до 9), каждая из которых принадлежит определенному разряду. Разрядность увеличивается справа налево (единицы, десятки, сотни, тысячи и т.д.).
Возьмем для примера число 249, которое можно представить в виде суммы произведений цифр на 10 в степени, соответствующей данному разряду:
Таким образом, нулевой разряд — это единицы (10 0 ), первый — десятки (10 1 ), второй — сотни (10 2 ) и так далее. В компьютере, как и в других электронных устройствах, вся информация распределяется по файлам (здесь о файловой системе подробности) и кодируется соответствующим образом в цифровом формате, причем в силу простоты использования применяется двоичная система счисления, на которой остановлюсь отдельно.
В двоичной системе числа представляются посредством всего двух цифр: 0 и 1. Попробуем записать уже рассмотренное нами число 249 в двоичной системе, чтобы понять ее суть. Для этого делим его на 2, получив целое частное с остатком 1. Эта единичка и будет самым младшим разрядом, который будет, как и в случае десятичной системы, крайним справа.
Далее продолжаем операцию деления и каждый раз целые числа также делим на 2, получая при этом в остатке 0 или 1. Их последовательно и записываем справа налево, получив в итоге 249 в двоичной системе. Деленин следует проводить до тех пор, пока в итоге не появится нуль:
Теперь записываем нули и единички в остатке последовательно справа налево и получаем наше подопытное число в двоичной системе:
Чтобы не осталось темных пятен, проведем обратное действие и попробуем перевести то же самое число из двоичной в десятичную систему, проверив заодно правильность выше изложенных действий. Для этого умножаем опять же по порядку слева направо нуль или единицу на 2 в степени, соответствующей разряду (по аналогии с десятичной системой):
Как видите все получилось, и мы смогли преобразовать число, записанное в двоичной системе, на его запись в десятичной системе счисления.
Соотношение битов и байтов в информатике
Я не зря предоставил чуть выше краткий математический экскурс, поскольку именно двоичная система служит основой измерения, используемой в электронных устройствах. Базовой единицей количества информации, равной разряду в двоичной системе, как раз и является бит.
Этот термин происходит от английского словосочетания binary digit (bit), что означает двоичное число. Таким образом, бит может принимать лишь только два возможных значения: 0 или 1. В информатике это означает два совершенно равных с точки зрения вероятности результата («да» или «нет») и при этом не допускается никакого другого толкования.
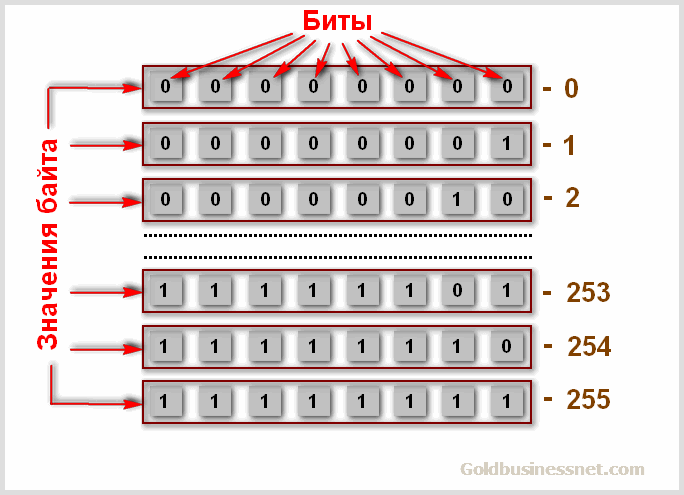
Это очень важно с точки зрения корректной работы системы. Двигаемся дальше. Количество бит, которое обрабатывается компьютером в один момент, называется байтом (byte). 1 байт равен 8 битам и, соответственно, может принимать одно из 2 8 (256) значений, то есть от 0 до 255:
Итак, нам теперь доподлинно известно, что такое байт, и какую роль он играет в качестве единицы измерения при работе с информацией, хранящейся и обрабатываемой в цифровом виде. Кстати, в международном формате байт может обозначаться двумя способами — byte или B.
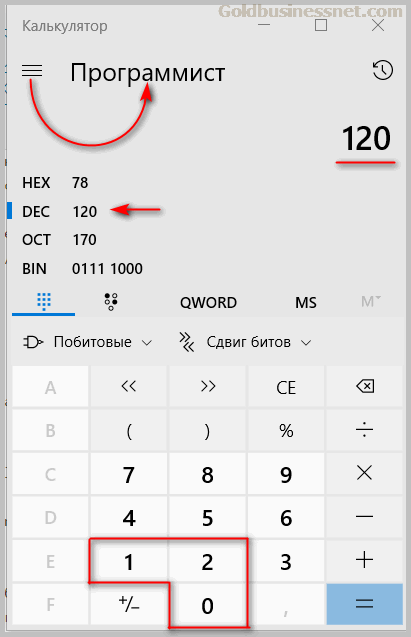
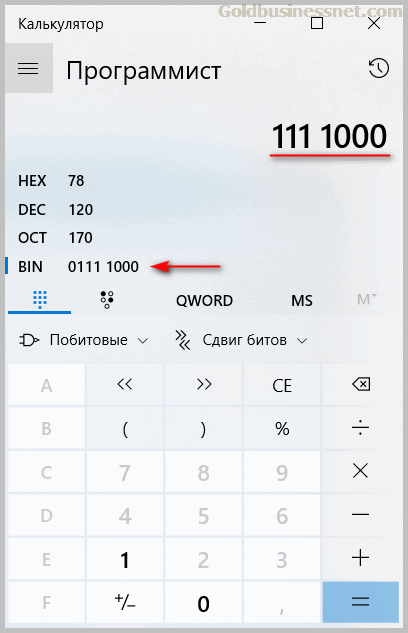
В меню «Вид» выбираете формат «Программист» и вводите желаемое число (например, 120):
Напротив опции «BIN» мы видим запись данного числа в двоичной системе:
На что здесь следует обратить внимание? Во-первых, в строке справа вверху представлены лишь семь разрядов (биты со значениями ноль или единица):
Здесь все просто. Если самый старший разряд (бит), расположенный крайним слева, принимает значение 0, то он просто не записывается. Два или более нулевых бита тоже опускаются (по аналогии с десятичными числами — ведь к сотням мы не прописываем 0 тысяч, например).
Доказательством может служить полная запись полученного числа напротив «BIN»:
Если вы внимательны, то увидите, что здесь во-вторых. Это способ записи в виде двух частей, каждая из которых состоит из четырех бит. В информатике используется еще такое понятие как полубайт, или ниббл (nibble). Это удобно тем, что ниббл можно представить как разряд в шестнадцатеричной системе, которая широко используется в программировании.
Понятие машинного слова
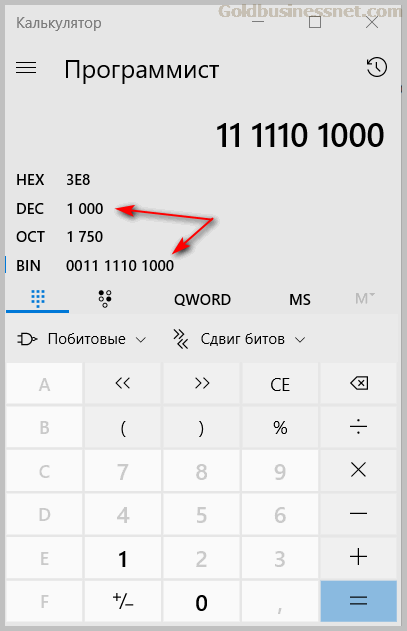
Выше мы поговорили о том, что байт содержит восемь бит. Это позволяет выразить 256 (два в восьмой степени) разных значений. Однако на практике в основном этого далеко не достаточно и во многих случаях приходится использовать не один, а несколько byte. В качестве примера воспользуемся еще раз калькулятором Windows и переведем число 1000 в двоичную систему:
Как видите, для этого пришлось отщипнуть пару разрядов из второго байта. На практике для обработки достаточно объемной информации в компьютерах применяется такое понятие как машинное слово, которое может содержать 16, 32, 64 bit.
Сколько байт в килобайте, мегабайте, гигабайте, терабайте
А теперь самое время перейти к производным байта и представить, какие приставки увеличения здесь используются. Ведь байт как единица очень маленькая величина, и для удобства очень даже полезно использовать аналоги, которые бы обозначали 1000 B, 1 000 000 B и т.д. Здесь тоже есть свои нюансы, о которых и поговорим ниже.
Строго говоря, для представления величин корректно использовать приставки для двоичной системы счисления, которые кратны 2 10 (1024). Это кибибайт, мебибайт, гебибайт и т.д.
Но данные словосочетания не прижились в широком использовании. Возможно, одной из причин стала их неблагозвучность. Поэтому пользователи (и не только) повсеместно употребляют вместо двоичных десятеричные приставки (килобайты, мегабайты, гигабайты, терабайты), что является не совсем корректным, поскольку по сути (в соответствии с правилами десятичной системы счисления) это означает следующее:
Но раз уж так сложилось, ничего не поделаешь. Важно лишь помнить, что на практике часто используются килобайт (Кбайт), мегабайт (Мбайт), гигабайт (Гбайт), терабайт (Тбайт) именно в качестве производных от байта как единицы измерения информации в двоичной системе. И в этом случае употребляют, например, термин «килобайт», имея ввиду именно 1024 байт.
Однако, очень часто производители накопителей (включая жесткие диски, флэшки, DVD- и CD-диски) при указании объема для хранения информации применяют именно десятичные приставки по прямому назначению (1 Кбайт = 1000 байт), в то время как тот же Виндовс, например, рассчитывает их размер в двоичной системе.
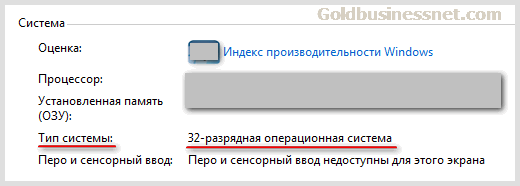
Отсюда и выходит некоторое несоответствие, которое может запутать простого пользователя. Скажем, в документации указана емкость диска 500 Гб, в то время как Windows показывает его объем равным 466,65 Гбайт.
По сути никакого расхождения нет, просто размер накопителя присутствует в разных системах счисления (тот же пень, только сбоку). Для неопытных юзеров это крайне неудобно, но, как я уже сказал, приходится с этим мириться.
Резюмируя, отмечу следующее. Скажем, вам зададут вопрос: сколько байт в килобайте? Теоретически корректным будет ответ: 1 килобайт равен 1000 байтам. Просто надо помнить, что на практике по большей части десятичные приставки используются в качестве двоичных, которые кратны 1024, хотя иногда они применяются по прямому назначению и кратны именно 1000.
Вот такая арифметика, надеюсь, что вы не запутались. В публикации я упомянул килобайт, мегабайт, гигабайт и терабайт, а что дальше? Какие еще более крупные единицы количества информации возможны? На этот вопрос ответит таблица, где указаны не только соотношение единиц в обеих системах, но и их обозначения в международном и российском форматах:
| Двоичная система | Десятичная система | ||||||
|---|---|---|---|---|---|---|---|
| Название | Обозначение | Степень | Название | Обозначение | Степень | ||
| Рос. | Межд. | Рос. | Межд. | ||||
| байт | Б | B | 2 0 | байт | Б | B | 10 0 |
| кибибайт | КиБ | KiB | 2 10 | килобайт | Кбайт | KB | 10 3 |
| мебибайт | МиБ | MiB | 2 20 | мегабайт | Мбайт | MB | 10 6 |
| гибибайт | ГиБ | GiB | 2 30 | гигабайт | Гбайт | GB | 10 9 |
| тебибайт | ТиБ | TiB | 2 40 | терабайт | Тбайт | TB | 10 12 |
| пебибайт | ПиБ | PiB | 2 50 | петабайт | Пбайт | PB | 10 15 |
| эксбибайт | ЭиБ | EiB | 2 60 | эксабайт | Эбайт | EB | 10 18 |
| зебибайт | ЗиБ | ZiB | 2 70 | зеттабайт | Збайт | ZB | 10 21 |
| йобибайт | ЙиБ | YiB | 2 80 | йоттабайт | Ибайт | YB | 10 24 |
Ежели желаете быстро определить, например, сколько мегабайт в гигабайте (хотя опытный юзер легко обойдется в этом случае без таблицы), то ищите в таблице ячейки, соответствующее числу байт в мегабайте и гигабайте, а затем делите большее значение на меньшее.
Получается, что в 1 гигабайте 1000 мегабайт. Точно также можно переводить производные в двоичной системе — мебибайты в кибибайты, тебибайты в гибибайты и т.д.
Используем конвертер для перевода битов и байтов
Публикация была бы неполной, если бы я не привел инструмент, с помощью которого можно осуществить перевод byte в различные производные. В сети много разнообразных конвертеров, посредством которых можно произвести эти операции. Вот один из них, который мне приглянулся.
Этот конвертер удобен тем, что введя количество byte, можно сразу получить результат во всех возможных измерениях (в том числе перевести биты в байты):
Из данного примера следует, что 3072 байта равно 24576 битам, 3,0720 килобайтам или 3 кибибайтам. Кроме этого, чуть ниже расположены ссылки на миникалькуляторы, где вы сможете быстро произвести конкретный перевод из одной системы единиц в другую.
Что такое байт килобайт мегабайт гигабайт информатика
Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
Байт – основная единица измерения количества информации.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события (N=4).
По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (2 5 =32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log2101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Задача 7.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.