Что такое абстрактный автомат
Абстрактный автомат
Абстра́ктный автома́т (в теории алгоритмов) — математическая абстракция, модель дискретного устройства, имеющего один вход, один выход и в каждый момент времени находящегося в одном состоянии из множества возможных. На вход этому устройству поступают символы одного алфавита, на выходе оно выдаёт символы (в общем случае) другого алфавита.
Формально абстрактный автомат определяется как пятерка
Где S — конечное множество состояний автомата, X, Y — конечные входной и выходной алфавиты соответственно, из которых формируются строки, считываемые и выдаваемые автоматом, 

Абстрактный автомат с выделенным начальным состоянием называется инициальным автоматом. Таким образом, абстрактный автомат определяет семейство инициальных автоматов
Если функции переходов и выходов однозначно определены для каждой пары 
Если функция переходов и/или функция выходов являются случайными, то автомат называют вероятностным.
Ограничение числа параметров абстрактного автомата определило такое понятие как конечный автомат.
Функционирование автомата состоит в порождении двух последовательностей: последовательности очередных состояний автомата 


Функционирование автомата в дискретные моменты времени t может быть описано системой рекуррентных соотношений:
Для уточнения свойств абстрактных автоматов введена классификация.
Абстрактные автоматы образуют фундаментальный класс дискретных моделей как самостоятельная модель, и как основная компонента машин Тьюринга, автоматов с магазинной памятью, конечных автоматов и других преобразователей информации.
Модель абстрактного автомата широко используется, как базовая, для построения дискретных моделей автоматов, распознающих, порождающих и преобразующих последовательности символов.
Полезное
Смотреть что такое «Абстрактный автомат» в других словарях:
абстрактный автомат — abstraktusis automatas statusas T sritis automatika atitikmenys: angl. abstract automaton vok. abstrakter Automat, m rus. абстрактный автомат, m pranc. automate abstrait, m … Automatikos terminų žodynas
Автомат — В Викисловаре есть статья «автомат» Автомат: Автомат устройство, самостоятельно выполняющее некоторые действия … Википедия
Конечный автомат — Конечный автомат абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию. Существуют различные варианты задания конечного автомата. Например,… … Википедия
ТЬЮРИНГА, МАШИНА — Абстрактный автомат (то есть компьютер или другой точный, определенный механизм), теоретически охарактеризованный британским математиком Аланом М. Тьюрингом в 1930 х гг. В основном, машина Тьюринга состоит из ленты и считывающей головки. Лента… … Толковый словарь по психологии
Теория автоматов — [automata theory] раздел теоретической кибернетики, который изучает математические модели (называемые здесь автоматами или машинами) реальных или возможных устройств, перерабатывающих дискретную информацию дискретными же тактами. Основными… … Экономико-математический словарь
Теория автоматов — [automata theory] раздел теоретической кибернетики, который изучает математические модели (называемые здесь автоматами или машинами) реальных или возможных устройств, перерабатывающих дискретную информацию дискретными же тактами. Основными… … Экономико-математический словарь
теория автоматов — Раздел теоретической кибернетики, который изучает математические модели (называемые здесь автоматами или машинами) реальных или возможных устройств, перерабатывающих дискретную информацию дискретными же тактами. Основными понятиями этой теории… … Справочник технического переводчика
Теория автоматов — Теория автоматов раздел дискретной математики, изучающий абстрактные автоматы вычислительные машины, представленные в виде математических моделей и задачи, которые они могут решать. Теория автоматов наиболее тесно связана с… … Википедия
Компьютер — Схема персонального компьютера: 1. Монитор 2. Материнская плата 3 … Википедия
Формальные методы — Пример формальной спецификации с использованием Z нотации В информатике и инженерии программного обеспечения формальными методами называется группа техник, основанных на математическом аппарате для … Википедия
Самостоятельное изучение схемотехники. Абстрактный автомат. Часть 2
Статья написана, собрана и сверстана Brotherofken. Спасибо ему огромное.
В предыдущей статье я попытался изложить все основные определения и принципы, чтобы сделать эту статью максимально понятной. Все не уместилось, так что я настоятельно советую ознакомиться с этими файлами:
Базис, Базис2, Минимизация. Далее в этой статье я оставил несколько разъясняющих пометок курсивом.
В этой статье я попробую объяснить доступным языком что такое абстрактный автомат, способы его представления. Так как теория автоматов полна математики и сложна, постараюсь писать человеческим языком, чтобы неподготовленный читатель смог понять о чём идёт речь.
Абстрактный автомат
Автомат должен будет реализовывать некоторые функции, которые заданы разработчиком. Он может быть простым сумматором, может реализовывать какую-либо микрокоманду процессора, выбирать слова из оперативной памяти или заниматься синтаксическим анализом выражения.
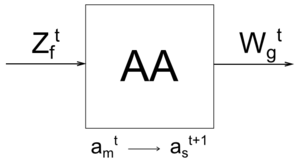
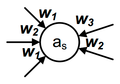
В общем виде, не вдаваясь в подробности, абстрактный автомат можно представить следующим образом:
Или, если перейти от иллюстрации к математическому описанию:
A =
Такой автомат функционирует дискретно по времени, то есть значения входов, выходов и внутреннее состояние автомата изменяются в дискретные моменты времени.
Итак мы в общем виде описали что есть Абстрактный автомат. Примером такого автомата может быть триггер, регистр ЭВМ или сумматор.
Т.е. автомат типа Мили вырабатывает выходной сигнал когда у него меняется входной, в зависимости от его предыдущего состояния. При этом длительность выходного сигнала не зависит от длительности входного, а только от его присутствия. В автоматах типа Мура выходной сигнал зависит от состояния автомата в текущий момент времени т.е. автомат будет вырабатывать определенный выходной сигнал пока не изменит свое состояние.
Способы задания автоматов
Как мы выяснили в первой части — автомат представляет собой совокупность входного и выходного алфавитов, множества внутренних состояний и функций, определяющих переходы и выходы. Однако, обычно функции δ и λ не заданы, и поведение автомата приходится описывать по-другому.
Графы
Граф автомата – это ориентированный связный граф, вершины которого символизируют внутренние состояния автомата, а дуги – переходы из одного состояния в другое.

Для графа Мили на дугах указываются сходные и выходные буквы. Выходные буквы пишутся над дугами, символизируя то, что выходное состояние зависит от состояния автомата в предыдущий момент времени.

Для графа автомата Мура на дугах записываются только входные буквы, выходные же указываются около вершин.
Важный момент: Если из каждой вершины выходит столько дуг, сколько есть входных букв, то автомат называется полным. Другими словами – если из каждой вершины определены переходы для каждой входной буквы. В наших примерах автомат Мили является полным, а автомат Мура – частичным.
И ещё: Если из одной вершины выходит дуг больше, чем входных букв (то есть 2 и более дуг с одинаковыми входными буквами), то такой автомат называется недетерминированным. Такое может произойти при построении формализованного описания и тогда надо будет произвести переход к детерминированному автомату, но это не всегда можно выполнить. Описание этого процесса я тоже упускаю, сразу нарисовав детерминированный автомат.
На этом о графах всё.
Таблицы переходов и выходов.
Графы нагляднее для человека, а таблицы — для машины. Любой автомат можно представить в виде таблицы переходов и выходов (ТПВ). В ТПВ строками являются внутренние состояния автомата, а столбцами – входные буквы.
Построим ТПВ для наших графов Мили и Мура. Если не определена какая-либо входная или выходная буква, то вместо неё ставится прочерк. Если не определено состояние, то действует это же простое правило.
ТПВ графа Мили
В ТПВ Мили в каждой клетке записаны переходы и выходы. Например, если автомат находится в состоянии С0 и на вход приходит буква a1, то он перейдёт в состояние С1 и на выходе появится буква b3.
ТПВ графа Мура
Для графа Мура строят отмеченную таблицу переходов. Выделяется дополнительный столбец для выходных букв.
В клетке под входной буквой пишется в какое состояние автомат переходит, в крайней правой клетке — какую выходную букву возвращает.
Пример синтеза автомата
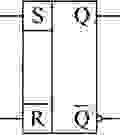
При помощи абстрактных автоматов можно описать практически что угодно. Можно описать работу цифровой схемы, а можно – синтаксический или лексический анализатор. Попробуем описать триггер – чем не автомат?
Чтобы задать граф нужно словесное описание алгоритма работы триггера. Читаем:
Кодируем входной и выходной алфавиты:
A =
B =
Строим граф автомата Мили: 
Вот такая забавная чебурашка получилась :-). Теперь можно построить таблицу переходов и выходов: 
Если расписать эту таблицу преобразовав условные обозначения в фактические, то получим таблицу которая представляет из себя таблицу переходов триггера. Затем её можно упростить:
Нанесём полученную функцию на карту Вейча и минимизируем:
Выпишем, что получилось: 
Строим по функции схему (Выполняли домашнее задание?): 
Немного непривычно видеть триггер в булевом базисе, поэтому переведём функцию в базис И-НЕ и нарисуем схему в нём: 
А на схеме асинхронный RS триггер обозначается вот так:
Теперь если приложить немного старания, то можно самостоятельно синтезировать простую новогоднюю гирлянду.
Абстрактный автомат
Из Википедии — свободной энциклопедии
Абстра́ктный автома́т (в теории алгоритмов) — математическая абстракция, модель дискретного устройства, имеющего один вход, два выхода и в каждый момент времени находящегося в одном состоянии из множества возможных. На вход этому устройству поступают символы одного алфавита, на выходе оно выдаёт символы (в общем случае) другого алфавита.
Формально абстрактный автомат определяется как шестёрка
Абстрактный автомат с выделенным начальным состоянием называется инициальным автоматом. Таким образом, абстрактный автомат определяет семейство инициальных автоматов
Если функция переходов и/или функция выходов являются случайными, то автомат называют вероятностным.
Ограничение числа состояний абстрактного автомата определило такое понятие как конечный автомат.
Для уточнения свойств абстрактных автоматов введена классификация.
Абстрактные автоматы образуют фундаментальный класс дискретных моделей как самостоятельная модель, и как основная компонента машин Тьюринга, автоматов с магазинной памятью, конечных автоматов и других преобразователей информации.
Модель абстрактного автомата широко используется, как базовая, для построения дискретных моделей автоматов, распознающих, порождающих и преобразующих последовательности символов.
Автоматы Мура и Мили
Выходные сигналы АА зависят от того, что поступало на его вход раньше.
Рассмотрим функционирование автоматов Мура и Мили.
[math]a(t+1) = \delta (a(t), z(t))[/math]
[math]w(t) = \lambda (a(t), z(t))[/math]
[math]a(t+1) = \delta (a(t), z(t))[/math]
[math]w(t) = \lambda (a(t))[/math]
В автоматах Мура выходные воздействия записаны на состояниях, а в автомате Мили — на переходах.
Содержание
Применение автоматов Мура и Мили [ править ]
Автоматы Мура и Мили широко применяются при проектировании цифровых устройств на основе программируемых логических интегральных схем (ПЛИС).
Наличие минимальной выходной задержки, связанной с переключением выходного регистра, отсутствие нестабильности переходного процесса на выходе автомата, отсутствие сквозного распространения сигнала через комбинационную схему от входа до выхода автомата, простота описания на языках описания аппаратуры HDL делает автомат Мура практически незаменимым.
Также автоматы Мура и взаимодействующие автоматы Мили используются в генетическом программировании (например, для решения задачи об «Умном муравье» [1] ).
Автомат, регулирующий пешеходный переход [ править ]
Рассмотрим автомат, регулирующий пешеходный переход по запросу пешеходов. Внешние события автомата — это события нажатия пешеходами кнопки-запроса на тротуаре и исчерпание тайм-аута. Автомат строится как автомат Мура, в котором выход — регулирование светофора и разрешающий сигнал на переход — это потенциальные сигналы, являющиеся функциями состояния.
Торговый автомат [ править ]
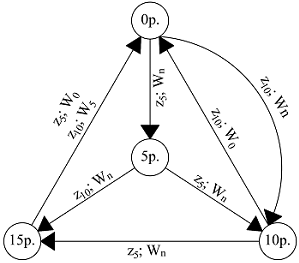
В качестве примера применения автомата Мили рассмотрим автомат по продаже шоколадок стоимостью [math]20[/math] рублей, принимающий монеты номиналом в [math]5[/math] и [math]10[/math] рублей и возвращающий сдачу, если это необходимо.
Входных сигналов [math]Z[/math] два: [math]Z_5[/math] — [math]5[/math] рублей и [math]Z_<10>[/math] — [math]10[/math] рублей.
Выходных сигналов [math]W[/math] три: [math]W_
Способы задания автоматов [ править ]
Табличный способ задания автомата Мили [ править ]
Автомат Мили может быть задан таблицей переходов и таблицей выходов.
| [math]a_ | ||
| [math]z_ | [math]a_ | [math]=\delta (a_ |
| [math]a_ | ||
| [math]z_ | [math]w_ | [math]=\lambda (a_ |
Пример: Задание автомата Мили табличным способом (автомат имеет два входных сигнала, два выходных сигнала и три состояния).
| [math]\delta[/math] | [math]a_<1>[/math] | [math]a_<2>[/math] | [math]a_<3>[/math] |
| [math]z_<1>[/math] | [math]a_<1>[/math] | [math]a_<3>[/math] | [math]a_<1>[/math] |
| [math]z_<2>[/math] | [math]a_<2>[/math] | [math]a_<1>[/math] | [math]a_<2>[/math] |
| [math]\lambda[/math] | [math]a_<1>[/math] | [math]a_<2>[/math] | [math]a_<3>[/math] |
| [math]z_<1>[/math] | [math]w_<2>[/math] | [math]w_<2>[/math] | [math]w_<2>[/math] |
| [math]z_<2>[/math] | [math]w_<1>[/math] | [math]w_<1>[/math] | [math]w_<2>[/math] |
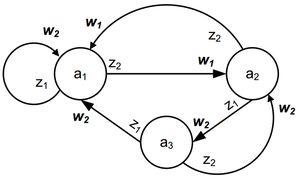
Графический способ задания автомата Мили [ править ]
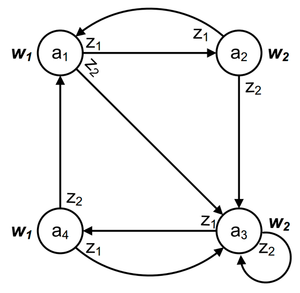
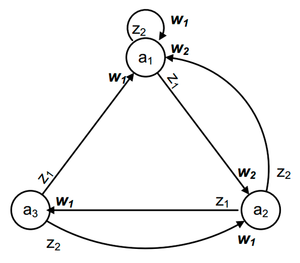
На рисунке приведен граф автомата Мили на 3 состояния, имеющий 2 входных сигнала и 2 выходных сигнала (см. предыдущий пример).
Табличный способ задания автомата Мура [ править ]
В автомате Мура выходной сигнал зависит только от состояния автомата и не зависит от входного сигнала.
Поэтому достаточно для задания автомата Мура в таблице переходов добавить одну строку.
| [math]\lambda[/math] | [math]w_<1>[/math] | [math]w_<2>[/math] | [math]w_<1>[/math] | [math]w_<2>[/math] | [math]w_<2>[/math] |
| [math]\delta[/math] | [math]a_<1>[/math] | [math]a_<2>[/math] | [math]a_<3>[/math] | [math]a_<4>[/math] | [math]a_<5>[/math] |
| [math]z_<1>[/math] | [math]a_<2>[/math] | [math]a_<2>[/math] | [math]a_<5>[/math] | [math]a_<5>[/math] | [math]a_<2>[/math] |
| [math]z_<2>[/math] | [math]a_<3>[/math] | [math]a_<3>[/math] | [math]a_<1>[/math] | [math]a_<1>[/math] | [math]a_<4>[/math] |
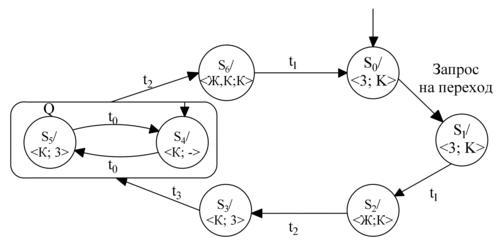
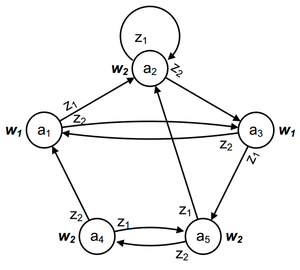
Графический способ задания автомата Мура [ править ]
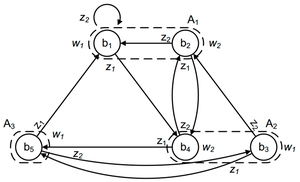
На рисунке приведен граф автомата Мура на 5 состояний, имеющий 2 входных сигнала и 2 выходных сигнала.
Реакция автоматов на входное слово [ править ]
Автомат Мили [ править ]
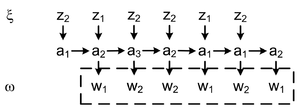
Допустим, входное слово [math]\xi[/math] поступает на вход автомата буква за буквой.
Выходное слово [math]\omega[/math] называется реакцией автомата Мили на входное слово [math]\xi[/math] в состоянии [math]a_<1>[/math] строится по таблице переходов и выходов).
Реакцию автомата на входное слово [math]\xi[/math] можно заменить обходом графа.
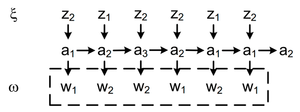
Автомат Мура [ править ]
В рассматриваемом примере для автоматов Мили и Мура реакции автоматов на одинаковое входное слово совпадают, но они сдвинуты на один такт. Автоматы Мили и Мура дающие одинаковые реакции на одинаковые входные слова называются эквивалентными. Данное замечание приводит к задаче построения эквивалентных автоматов, дающих одинаковые реакции на одинаковые входные слова.
Эквивалентность автоматов Мили и Мура [ править ]
Автомат Мура переходит в автомат Мили, если всем переходам в состояние поставить выходные воздействия этого состояния. После таких преобразований получим эквивалентный автомат Мили.
Однако, чтобы преобразовать автомат Мили в автомат Мура такой алгоритм не подходит, т.к. в одно состояние могут вести разные переходы. Но можно просто добавить новых состояний, устанавливая необходимые соответствия.
Далее будет приведено формальное доказательство факта эквивалентности с явным предъявлением конструкции.
| Теорема (Эквивалентность автоматов Мура и Мили): | |||||||
| Мура | Мили |
| [math]\delta _ (a_ | [math]\delta _ (a_ |
| [math]\lambda _(a_ | [math]\lambda _ (a_ |
 |  |
При переходе от автомата Мура к автомату Мили функции переходов также совпадают, а для определения функции выходов выходные сигналы с вершин опускается на входные дуги.
Проделав такие преобразования мы должны доказать, что получили автомат Мили, эквивалентный автомату Мура, т.е. что реакции автоматов на одинаковые входные воздействия совпадают.
При таком переходе (Мура к Мили) число состояний совпадает.
Таким образом, для выходной последовательности длины 1 поведение автоматов [math]S_<1>[/math] и [math]S_<2>[/math] полностью совпадает. Далее по индукции получаем эквивалентность автоматов.
Переход от автомата Мили к автомату Мура [ править ]
Требуется перейти к автомату Мура
Для определения алфавита состояний, функций переходов и выходов автомата Мура воспользуемся следующей вспомогательной таблицей.
| Мура | Мили |
 | [math]A_ |
| [math]a_<1>: A_ <1>= \left \ < \begin | [math]a_<2>: A_ <2>= \left \ < \begin | [math]a_<3>: A_ <3>= \< (a_<3>, w_<1>) \> = b_<5>[/math] |
При определении функции переходов результирующего автомата Мура из всех состояний, порожденных одним состоянием автомата Мили, должны быть переходы под воздействием одинаковых входных сигналов.
Поскольку в автомате Мура выходной сигнал зависит только от состояния автомата, то в примере рядом с состояниями проставим соответствующие выходные сигналы.
И так если осуществить следующие преобразования, то получим:
| Мили | Мура | Мили |
| [math]S_ <1>\rightarrow[/math] | [math]S_ <2>\rightarrow[/math] | [math]S_<3>[/math] |
| 3 состояния | 5 состояний | 5 состояний |
Методы взаимной транспозиции автоматов Мили и Мура показывают, что при переходе от автомата Мили к автомату Мура число состояний принципиально не меняется. В то время как при обратном переходе в автомат Мура число состояний, как правило, увеличивается. Вследствие транзитивности отношения эквивалентности два автомата Мили, первый из которых получен из автомата Мура, так же будут эквивалентны, но у второго автомата число состояний будет больше. Таким образом эквивалентные между собой автоматы могут иметь различное число состояний. В связи с чем и возникает задача нахождения минимального автомата в классе эквивалентных между собой автоматов. Существование для любого абстрактного автомата эквивалентного ему абстрактного автомата с минимальным числом внутренних состояний впервые было доказано Муром.