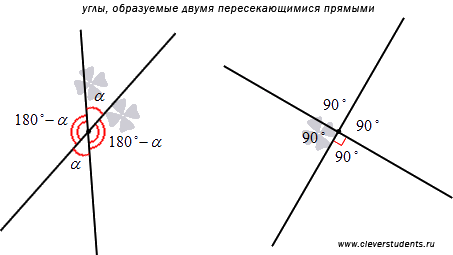
Что считается углом между двумя прямыми
Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
Из выражения (1.3) получим:
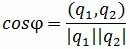 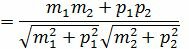 . . | (1.4) |
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
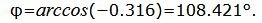 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
 |
Угол между прямыми равен:
 |
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
Сделаем преобразования с выражением (1.7):
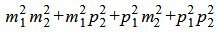 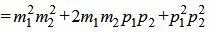 , , |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
Пример 2. Определить, параллельны ли прямые
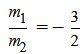 , , 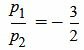 . . |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
Пример 3. Определить, перпендикулярны ли прямые
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
Из определения скалярного произведения двух векторов, имеем:
Из уравнения (19) получим
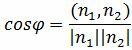 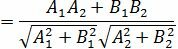 . . | (1.20) |
Пример 4. Найти угол между прямыми
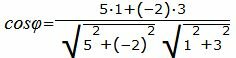 |
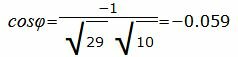 |
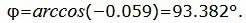 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
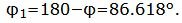 |
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
Из выражения (2.3) получим:
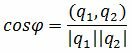 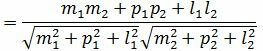 . . | (2.4) |
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
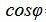 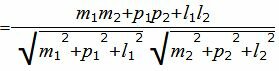 . . |
 |
Угол между прямыми равен:
 |
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
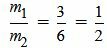 , , 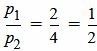 , , 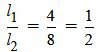 . . |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
Выражение (2.13) нужно понимать так:
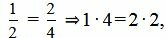 , , 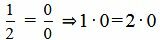 , , 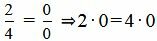 . . | (2.14) |
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
Пример 3. Определить, перпендикулярны ли прямые
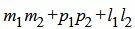 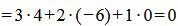 . . | (2.19) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Угол между пересекающимися прямыми – определение, примеры нахождения.
Начнем с краткого обзора материала статьи.
Сначала дано определение угла между пересекающимися прямыми с поясняющим рисунком. Далее показаны методы, позволяющие найти синус угла, косинус угла и сам угол между двумя пересекающимися прямыми на плоскости и в пространстве по известным уравнениям этих прямых в фиксированной прямоугольной системе координат, получены соответствующие формулы и приведены подробные решения примеров и задач.
Навигация по странице.
Чтобы определить угол между двумя пересекающимися прямыми нам потребуются определения, данные в статье геометрическая фигура угол и некоторые вспомогательные определения.
Две прямые называются пересекающимися, если они имеют одну единственную общую точку. Эта общая точка двух прямых называется точкой пересечения прямых. Точка пересечения разбивает каждую из пересекающихся прямых на два луча. Очевидно, эти лучи образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Таким образом, если нам известна мера одного из углов, образованных двумя пересекающимися прямыми, то мы можем определить меры трех остальных углов. Действительно, пусть один из углов равен углу 



Теперь можно переходить к определению угла между пересекающимися прямыми.
Угол между двумя пересекающимися прямыми – это мера меньшего из четырех углов, образованных этими прямыми.
Из приведенного определения следует, что градусная мера угла между двумя пересекающимися прямыми выражается действительным числом из интервала 
Нахождение угла между двумя пересекающимися прямыми на плоскости.
Существует множество разнообразных задач, в которых приходится находить угол между пересекающимися прямыми. В зависимости от условий этих задач подбирается подходящий метод решения.
Можно использовать методы геометрии. К примеру, если известны какие-либо дополнительные углы, то можно пробовать связать их с искомым углом между пересекающимися прямыми, отталкиваясь от равенства или подобия фигур. Если известны стороны треугольника и требуется найти угол между пересекающимися прямыми, на которых лежат стороны треугольника, то можно использовать теорему косинусов. При наличии прямоугольных треугольников отыскать угол между пересекающимися прямыми помогают определения синуса, косинуса и тангенса угла. Много подобных задач решается на уроках геометрии в средней школе.
Для нахождения углов между пересекающимися прямыми также прекрасно подходит метод координат. Давайте детально разберем его.
Решим поставленную задачу.
Мы знаем, что от прямой линии на плоскости в прямоугольной системе координат неотделим направляющий вектор прямой и нормальный вектор прямой, и мы можем по заданному уравнению прямой на плоскости определить координаты ее направляющего и нормального вектора. Таким образом, у нас есть возможность получить координаты направляющих и нормальных векторов заданных пересекающихся прямых.
Угол между заданными пересекающимися прямыми может быть найден через
Разберем каждый случай.
Разберем решение примера.
угол между указанными пересекающимися прямыми равен 45 градусам.
Основное тригонометрическое тождество позволяет найти синус угла при известном косинусе этого угла. Так как угол 

Тогда 
Осталось разобраться, как найти угол между пересекающимися прямыми, если известен направляющий вектор одной прямой и нормальный вектор другой прямой.
Если угол между векторами 





Так как косинусы равных углов равны, то последние равенства можно записать в виде 



(Обратите внимание: заданные прямые совпадают с прямыми из предыдущего примера).
Очевидно, получили такой же угол между пересекающимися прямыми, как и в предыдущем примере.
Дадим еще формулу для нахождения угла между двумя пересекающимися прямыми a и b через угловые коэффициенты этих прямых.
Определите угол между пересекающимися прямыми 

(В условии даны все те же пересекающиеся прямые из предыдущих примеров).
Заданные прямые имеют угловые коэффициенты 


В заключении этого пункта отметим, что совсем не обязательно запоминать все выведенные формулы для нахождения угла между пересекающимися прямыми на плоскости. Достаточно понимать, что угол между пересекающимися прямыми может быть найден с помощью угла между направляющими или нормальными векторами прямых, уметь определять координаты этих векторов по известным уравнениям прямых, а также помнить формулу для вычисления косинуса угла между двумя векторами.
Нахождение угла между двумя пересекающимися прямыми в пространстве.
Нахождение угла между двумя пересекающимися прямыми в пространстве методом координат сводится к нахождению координат направляющих векторов этих прямых и последующему определению угла между ними. При этом все рассуждения из предыдущего пункта, касающиеся определения угла между пересекающимися прямыми через угол между их направляющими векторами, остаются справедливыми.
Пусть искомый угол между пересекающимися прямыми равен 



Тогда искомый угол между пересекающимися прямыми равен 
Угол между прямыми
Определение угла между прямыми
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k 1· k 2 = 0), то прямые перпендикулярны.
Соответственно легко найти угол между прямыми
Угол между прямыми через направляющие векторы этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано параметрически
x = l t + a y = m t + b
то вектор направляющей имеет вид
Если уравнение прямой задано как
Если дано каноническое уравнение прямой
то вектор направляющей имеет вид
Если задано уравнение прямой с угловым коэффициентом
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =
Угол между прямыми через векторы нормалей этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано как
то вектор нормали имеет вид
Если задано уравнение прямой с угловым коэффициентом
то вектор нормали имеет вид
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
sin φ = | a · b | | a | · | b |
Примеры задач на вычисления угла между прямыми на плоскости
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор
cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
Угол между прямыми в пространстве
cos φ = | a · b | | a | · | b |
Если дано каноническое уравнение прямой
то направляющий вектор имеет вид
Если уравнение прямой задано параметрически
x = l t + a y = m t + b z = n t + c
то направляющий вектор имеет вид
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.
Преобразуем второе уравнение к каноническому вид.
Получено уравнение второй прямой в канонической форме